Kiindulási pontunk, mint általában, most is egy véletlen kísérlet a hozzá tartozó valószínűségi mezővel és az azon értelmezett valószínűségi mértékkel. Tegyük fel, hogy adott egy, a kísérlettől függő, értékű valószínűségi változó és egy függvény. Ekkor egy új, értékű valószínűségi változó. Ha ismerjük eloszlását, hogyan határozhatjuk meg eloszlását? Ez egy igen fontos és alapvető kérdés, és felszínesen szólva, a válasz sem bonyolult.
Igazoljuk, hogy amint .

Azonban nagyon gyakran eloszlása az eloszlásfüggvényével, vagy az sűrűségfüggvényével adott, és ugyanígy, eloszlás-, vagy sűrűségfüggvényét szeretnénk meghatározni. Ez általában nehéz feladat, mert ahogy látni fogjuk, viszonylag egyszerű eloszlások egyszerű transzformáltjai is komplex eloszlásokhoz vezethetnek. Ezt a problémát különböző speciális esetekben fogjuk kezelni.
Tegyük fel, hogy diszkrét eloszlású súlyfüggvénnyel (ekkor persze megszámlálható). Igazoljuk, hogy ekkor is diszkrét eloszlású, és súlyfüggvénye az alábbi függvény:
Tegyük fel, hogy folytonos eloszlású az halmazon sűrűségfüggvénnyel, és megszámlálható. Igazoljuk, hogy ekkor diszkrét eloszlású, és súlyfüggvénye az alábbi függvény:
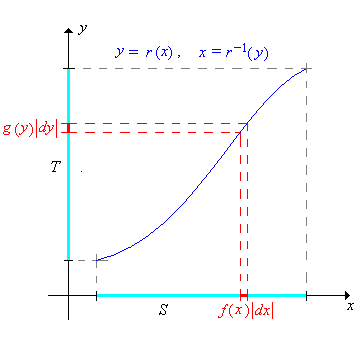
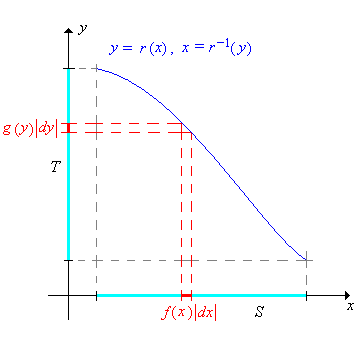
Tegyük fel, hogy folytonos eloszlású az halmazon, pedig folytonos eloszlású -en. Tegyük fel továbbá, hogy ismerjük az változó sűrűségfüggvényét. Nagyon gyakran sűrűségfüggvényét meghatározhatjuk úgy, hogy először az eloszlásfüggvényét határozzuk meg, majd azt deriváljuk. Ezt a módszert fogjuk eloszlásfüggvény módszernek nevezni.
Ha az transzformáció kölcsönösen egyértelmű és sima, akkor sűrűségfüggvénye közvetlen módon megkapható az sűrűségfüggvényéből az úgynevezett változócsere formulával.
Az egyszerűség kedvéért először csak ez egydimenziós esetet tárgyaljuk. Tegyük fel tehát hogy egy, az intervallumon folytonos eloszlású valószínűségi változó. Jelölje az eloszlásfüggvényét , a sűrűségfüggvényét pedig . Legyen továbbá , ahol az -ből egy intervallumra képező differenciálható függvény. Mint általában, jelölje az eloszlás-, pedig a sűrűségfüggvényét.
Tegyük fel, hogy szigorúan monoton növekedő -en. Igazoljuk, hogy -re
Tegyük fel, hogy szigorúan monoton csökkenő -en. Igazoljuk, hogy -re
A 4. és 5. feladatban szereplő formulákat kezelhetjük egységesen: ha egy szigorúan monoton függvény -en, akkor az változó sűrűségfüggvényére
Az jelöléssel a változócserére vonatkozó formula elegánsabban írható:
 |
 |
A fenti eredmény általánosítása egy többváltozós analízisbeli tétel. Tegyük fel, hogy egy -beli folytonos valószínűségi változó, a sűrűségfüggvénye pedig . Legyen , ahol kölcsönösen egyértelmű, -ből -re képező differenciálható függvény. Ekkor az inverz függvény első deriváltja egy -es mátrix, melynek elemei a parciális deriváltak:
Ezt a mátrixot Jacobi mátrixnak is nevezik (Karl Gustav Jacobi tiszteletére). A mátrix
determinánsa lesz a fontos számunkra, ugyanis a többváltozós változócserére vonatkozó formula állítása szerint a fenti feltételek mellett az változó sűrűségfüggvényére
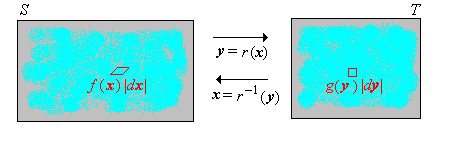
A lineáris transzformációk (vagy affin transzformációk) a legfontosabb és leggyakrabban előforduló transzformációk. Ilyenek esetén az előző változócserére vonatkozó képlet egy egyszerűbb, speciális alakja is igaz. Tegyük fel, hogy egy értékű folytonos valószínűségi változó sűrűségfüggvénnyel. Legyen , ahol és . Ekkor persze értékeit a halmazon veszi fel.
Az előbb igazolt változócserére vonatkozó képlet alapján igazoljuk, hogy sűrűségfüggvénye:
Vegyük észre, hogy ha , akkor sűrűségfüggvénye nagyon hasonlít sűrűségfüggvényére, szemléletesen csak annyit csináltunk, hogy másképp skáláztuk a vízszintes tengelyt. Ekkor mondhatjuk azt, hogy az átskálázott változata. Ilyen transzformációkkal találkozunk majd a Nevezetes eloszlások fejezetben.
Az előző formula többváltozós változata sem bonyolult, csak ott mátrixokat és vektorokat kell használnunk. Legyen tehát egy értékű folytonos valószínűségi változó sűrűségfüggvénnyel, és legyen , ahol és egy invertálható méretű mátrix. Ekkor persze a halmazban veszi fel az értékeit.
Igazoljuk, hogy
A változócserére vonatkozó képlet alapján igazoljuk, hogy sűrűségfüggvénye
Nagyon gyakori a valószínűségszámításban, hogy két valószínűségi változó összegének eloszlását szeretnénk meghatározni. Legyenek tehát és egy közös kísérlettől függő valós értékű valószínűségi változók. Célunk eloszlásának meghatározása.
Tegyük fel, hogy diszkrét eloszlásúak valamilyen súlyfüggvénnyel. Igazoljuk, hogy is diszkrét eloszlású az alábbi súlyfüggvénnyel:
Az előző formulában az összegzés igazából az megszámlálható halmazon történik.
Tegyük fel, hogy folytonos eloszlásúak valamilyen sűrűségfüggvénnyel. Igazoljuk, hogy is folytonos eloszlású az alábbi sűrűségfüggvénnyel:
Messze a legfontosabb az az eset, amikor és függetlenek.
Tegyük fel, hogy és független diszkrét eloszlású valószínűségi változók és súlyfüggvényekkel. Igazoljuk, hogy súlyfüggvénye:
Az előző formulában az összegzés igazából az megszámlálható halmazon történik. Az előző feladatban definiált függvényt nevezik a és függvények (diszkrét) konvolúciójának.
Tegyük fel, hogy és független folytonos eloszlású valószínűségi változók és sűrűségfüggvényekkel. Igazoljuk, hogy sűrűségfüggvénye:
Az előző formulában az integrálást igazából az halmazon tekintjük. Az sűrűségfüggvényt nevezzük az és függvények folytonos konvolúciójának.
Igazoljuk, hogy a konvolúció (akár diszkrét,akár folytonos) teljesíti az alábbi tulajdonságokat (ahol , . és valószínűségi súly-, vagy sűrűségfüggvények). Adjunk két bizonyítást: az egyiknél a konvolúciót definiáló formulát használjuk fel, a másiknál azt a tényt, hogy két független valószínűségi változó összegét tekintjük!
Tehát a (b) részben írhattunk volna -t, hisz ez egyértelműen definiált. Ha független, azonos eloszlású valószínűségi változók sorozata, melyek közös súly-, vagy sűrűségfüggvénye , akkor
súly-, vagy sűrűségfüggvénye , az függvény -szeres konvolúciója önmagával, vagy más szóval konvolúciós hatványa. Megfelelő skálázásokkal elég általános feltételek mellett igaz, hogy eloszlása konvergál a standard normális eloszláshoz, amint . Ennek az állításnak a pontos megfogalmazását nevezik centrális határeloszlás-tételnek, ami a valószínűségszámítás egyik legfontosabb tétele. A centrális határeloszlás-tétellel részletesen a Véletlen minták című fejezetben foglalkozunk.
Tegyük fel, hogy független, azonos eloszlású valószínűségi változók sorozata. Sok alkalmazásban fontos ezek minimumának és maximumának eloszlása, ezért vezessük be az
jelöléseket. Például ahogy azt már régebben tárgyaltuk, a megbízhatóság elmélet alapmodelljében egy rendszer egymástól függetlenül üzemelő komponensből áll. Jelölje az -edik komponens élettartamát. Ekkor a soros kapcsolású rendszer élettartama, amely rendszer pontosan akkor üzemel, ha minden komponense üzemel. Hasonlóan, a párhuzamos kapcsolású rendszer élettartama, amely rendszer pontosan akkor üzemel, ha legalább egy komponense üzemel.
Különösen fontos az az eset, amikor a valószínűségi változók nemcsak függetlenek, de ráadásul azonos eloszlásúak. Ebben az esetben a valószínűségi változók sorozata egy elemű véletlen minta valamilyen háttéreloszlásból. Ekkor a legnagyobb és a legkisebb változóértékek vizsgálata a rendezett minták statisztikai vizsgálatának tárgya, erről részletesen a Véletlen minták fejezet rendezett minták statisztikájával foglalkozó részében olvashatunk.
Jelölje az változó eloszlásfüggvényét, ahol és legyen az , pedig a eloszlásfüggvénye.
Igazoljuk, hogy minden esetén
Igazoljuk, hogy minden esetén
A 14. feladat következménye, hogy eloszlásfüggvény szorzata is eloszlásfüggvény, a 15. feladat következménye pedig, hogy túlélési függvény szorzata is túlélési függvény. A megbízhatósági elméletben a változók nem negatívak és darab megbízhatósági függvény szorzata is megbízhatósági függvény. Ha folytonos eloszlású sűrűségfüggvénnyel minden esetén, akkor és is folytonos eloszlásúak, és sűrűségfüggvényük megkapható a 14., illetve 15. feladatban meghatározott eloszlásfüggvények deriválásával.
A formulák tovább egyszerűsödnek, ha az valószínűségi változók nemcsak függetlenek, de ráadásul azonos eloszlásúak is. Tegyük fel, hogy ez most teljesül, és jelölje a közös eloszlásfüggvényt.
Igazoljuk, hogy minden esetén
Speciálisan azt kaptuk, hogy egy eloszlásfüggvény pozitív egész hatványa is eloszlásfüggvény. Általánosabban is könnyű látni, hogy egy eloszlásfüggvény minden pozitív hatványa eloszlásfüggvény. Vajon hogyan lehetne ezt igazolni pusztán valószínűségszámítási érveléssel? Most a független, azonos eloszlású feltételek mellett tegyük még fel azt is, hogy az változók közös eloszlása folytonos valamilyen sűrűségfüggvénnyel. Jelölje az , pedig a változó sűrűségfüggvényét.
Igazoljuk, hogy minden esetén
Legyen folytonos eloszlású valós értékű valószínűségi változó eloszlás-, és sűrűségfüggvénnyel. Igazoljuk, hogy
Legyen az változó előjele (vagy más szóval szignuma), azaz
Tegyük fel, hogy az változó sűrűségfüggvénye szimmetrikus a nullára, azaz minden esetén. Igazoljuk, hogy
Ebben a részben számolásos feladatokat sorolunk fel, melyekben gyakran megjelenik eloszlások egy paraméteres családja. Mindig érdekesek az olyan esetek, amikor egy paraméteres eloszláscsalád egyik tagját transzformációval egy másik családba képezzük. Az is érdekes jelenség, ha egy paraméteres család zárt vagy invariáns változók bizonyos típusú transzformációira. Sokszor az ilyen jellegű tulajdonságok teszik számunkra igazán érdekessé az adott eloszláscsaládot. Az alábbi feladatok megoldása mellett törekedjünk arra is, hogy felismerjük, mely feladatokban találhatunk ilyen tulajdonságú eloszláscsaládokat!
Ahogy azt már korábban tárgyaltuk, a hagyományos kocka kifejezés egy hatoldalú dobókockát jelent. Az igazságos kocka olyan, amelyet ha feldobunk, minden oldalára azonos valószínűséggel esik. Az egy-hat irányban lapos kocka pedig feldobás után az 1 és a 6 értékeket , a többi értéket valószínűséggel mutatja.
Feldobtunk két hagyományos kockát, a dobott értékeket az vektor jelöli. Határozzuk meg súlyfüggvényét az alábbi esetekben:
A kockadobás kísérletben válasszunk két dobókockát és a dobott számok összegét. Szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus súlyfüggvény a valódi súlyfüggvényhez az alábbi esetekben:
Feldobtunk egy igazságos és egy egy-hat irányban lapos kockát. Határozzuk meg a dobott számok összegének súlyfüggvényét!
Feldobtunk hagyományos, igazságos kockát. Határozzuk meg az alábbi valószínűségi változók súlyfüggvényét:
A kockadobás kísérletben válasszunk igazságos kockákat és az alábbi valószínűségi változókat. Változtassuk értékét, és figyeljük meg, hogyan változik a súlyfüggvény alakja. Az speciális esetben szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus súlyfüggvény a valódi súlyfüggvényhez!
Legyen . Határozzuk meg és rajzoljuk le sűrűségfüggvényét az alábbi esetekben:
Hasonlítsuk össze az előző feladatban kapott eloszlásokat! Vegyük észre, hogy az olyan egyszerű eloszlásból is, mint az egyenletes eloszlás, viszonylag egyszerű transzformációval kaphatunk komplikált eloszlásokat. Másrészt viszont az egyenletes eloszláscsalád invariáns a lineáris transzformációkra.
Legyen egyenletes eloszlású az halmazon, és legyen , ahol és egy invertálható, méretű mátrix. Igazoljuk, hogy egyenletes eloszlású a halmazon!
Tegyük fel, hogy egyenletes eloszlású a négyzeten, és legyen .
Legyen független valószínűségi változók sorozata, melyek mindegyike egyenletes eloszlású a intervallumon. Határozzuk meg a következő valószínűségi változók sűrűségfüggvényét (ezek mindegyike béta eloszlású lesz).
A rendezett minták statisztikája kísérletben válasszuk az egyenletes eloszlást!
Jelölje a -en egyenletes eloszlás sűrűségfüggvényét! Határozzuk meg az és az függvényeket, majd rajzoljuk le a három függvényt egy közös koordinátarendszerbe! Vegyük észre, hogy a függvények egyre jobban hasonlítanak a centrális határeloszlás-tételben adott határfüggvényhez!
Fontos tény, hogy a intervallumon egyenletes eloszlásból transzformációval majdnem minden valós eloszlás megkapható. Ez különösen fontos a szimulációs feladatokban, hisz nagyon sok program képes véletlen szám generálásra, ami igazából -en egyenletes eloszlású valószínűségi változó közelítése. Megfordítva, minden olyan folytonos eloszlás, amely értékkészlete egy részhalmaza, áttranszformálható a intervallumon egyenletes eloszlásba.
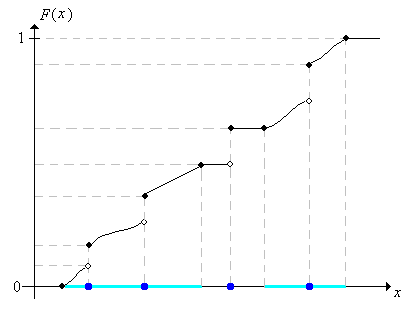
Tegyük fel először, hogy egy -en értelmezett eloszlás (amely lehet akár diszkrét, folytonos, vagy keverék) eloszlásfüggvénye, és legyen a kvantilis függvénye.
Legyen egyenletes eloszlású a intervallumon. Igazoljuk, hogy eloszlásfüggvénye .
Ha meg tudjuk határozni -et, akkor az előző feladat segítségével tudunk szimulálni egy olyan eloszlású valószínűségi változót, melynek eloszlásfüggvénye . Más szóval eloszlásfüggvényű valószínűségi változót szimulálhatunk úgy, hogy meghatározunk egy véletlen kvantilis értéket. Az általunk használt appletek többsége így szimulál valószínűségi változókat.
 |
 |
Tegyük fel, hogy folytonos eloszlású az intervallumon, és az eloszlásfüggvénye szigorúan monoton növekedő -en. Igazoljuk, hogy egyenletes eloszlású a intervallumon!
Hogyan tudnánk szimulálni egy tetszőleges intervallumon vett egyenletes eloszlást? Zsebszámológéppel szimuláljunk öt független, -en egyenletes eloszlású valószínűségi változót!
A Bernoulli kísérletsorozat egy független, azonos eloszlású indikátor valószínűségi változókból álló sorozat. Megbízhatóság elméleti jelölésekkel jelenti az -edik kísérlet kudarcát, míg jelenti, hogy az -edik kísérlet sikeres. A kísérletsorozat (vagy folyamat) egyetlen paramétere a siker valószínűsége, . Ezt a véletlen folyamatot Jacob Bernoulli-ról nevezték el; részletesebben a Bernoulli kísérletekről szóló fejezetben olvashatunk róla.
Igazoljuk, hogy a Bernoulli sorozatban lévő valószínűségi változók közös súlyfüggvénye .
Legyen a sikeres kísérletek száma az első kísérlet között. Valószínűségszámítási érveléssel (a függetlenséget is kihasználva) igazoljuk, hogy súlyfüggvényére igaz az alábbi képlet (ezzel definiálják az és paraméterű binomiális eloszlást):
Mint az előbb, legyen az első kísérlet között a sikeresek száma.
Speciálisan azt kaptuk, hogy ha és függetlenek, továbbá binomiális eloszlású és paraméterekkel, pedig és paraméterű binomiális eloszlású, akkor szintén binomiális eloszlású és paraméterekkel.
Határozzuk meg az elemből álló Bernoulli kísérlet sorozatban a sikeres kísérletek és sikertelen kísérletek száma különbségének valószínűségi súlyfüggvényét!
A paraméterű Poisson eloszlás súlyfüggvénye
Ezt az eloszlást Simeon Poisson-ról nevezték el, és nagyon gyakran használják időbeli, vagy térbeli véletlen pontok modellezésére. A Poisson eloszlást részletesen a A Poisson folyamatról szóló fejezetben tárgyaljuk.
Legyenek és független Poisson eloszlású valószínűségi változók, ahol paramétere , paramétere pedig . Igazoljuk, hogy egy paraméterű Poisson eloszlású változó, azaz . Segítség: Használjuk a binomiális tételt.
Az (ráta-)paraméterű exponenciális eloszlás sűrűségfüggvénye . Az exponenciális eloszlásokról részletesen a Poisson folyamatokról szóló fejezetben olvashatunk.
Hogyan szimulálhatunk egy egyenletes eloszlású véletlen szám segítségével paraméterű exponenciális eloszlású valószínűségi változót? Zsebszámológéppel szimuláljunk öt független paraméterű exponenciális eloszlású valószínűségi változót!
Legyen paraméterű exponenciális eloszlású. Határozzuk meg a következő valószínűségi változók súlyfüggvényét:
Vegyük észre, hogy az előző feladatban kapott eloszlások geometriai eloszlások -en, illetve -on. Sok szempontból a geometriai eloszlás olyan, mint az exponenciális eloszlás diszkrét változata.
Legyenek és független, 1 paraméterű exponenciális eloszlású valószínűségi változók, és legyen .
Legyenek és független, , illetve paraméterű exponenciális eloszlású valószínűségi változók. Határozzuk meg és rajzoljuk le sűrűségfüggvényét!
Legyenek független valószínűségi változók, ahol exponenciális eloszlású paraméterrel minden esetén.
Vegyük észre, hogy az (a) részben tekintett minimum exponenciális eloszlású paraméterrel. Ez azt jelenti, hogy ha egy soros kapcsolású rendszer minden alkatrésze független, exponenciális élettartamú, akkor maga a rendszer is exponenciális élettartamú, melynek paramétere az egyes komponensek paramétereinek összege.
A rendezett minták statisztikája kísérletben válasszuk az exponenciális eloszlást!
A 44. feladat jelöléseit használva igazoljuk, hogy minden esetén
Az előző feladat eredménye alapvető fontosságú a folytonos idejű Markov láncok elméletében.
Az paraméterű gamma eloszlás (ahol ) sűrűségfüggvénye:
Ilyen eloszlásokat használnak az érkezési (felújítási) idők modellezésére bizonyos feltevések esetén. A gamma eloszlásról részletesen a Poisson folyamatokról szóló fejezetben olvashatunk.
Igazoljuk, hogy paraméterű, pedig paraméterű gamma eloszlású, továbbá és függetlenek, akkor szintén gamma eloszlású, paraméterrel. Azaz lássuk be, hogy .
Az paraméterű Pareto eloszlás sűrűségfüggvénye:
Ezt az eloszlást (amely Vilfredo Pareto-ról kapta a nevét) gyakran alkalmazzák a bevétel, vagy más pénzügyi mennyiségek modellezésére. Részletes tárgyalása a Nevezetes eloszlások című fejezet Pareto eloszlással foglalkozó részében található.
Legyen paraméterű Pareto eloszlású. Határozzuk meg az eloszlását! Vegyük észre, hogy ez épp az paraméterű exponenciális eloszlás!
Legyen paraméterű Pareto eloszlású. Határozzuk meg sűrűségfüggvényét! Ekkor eloszlása béta eloszlás, és paraméterekkel.
Hogyan tudnánk egyetlen egyenletes eloszlású véletlen szám segítségével tetszőleges paraméterű Pareto eloszlást szimulálni? Zsebszámológéppel szimuláljunk öt független, paraméterű Pareto eloszlású valószínűségi változót!
A standard normális eloszlás sűrűségfüggvénye
Tegyük fel, hogy standard normális eloszlású, és legyenek , és . Határozzuk meg és rajzoljuk le az változó sűrűségfüggvényét!
Az valószínűségi változó eloszlását nevezik hely-paraméterű, és skála-paraméterű normális eloszlásnak. (Mint azt később látni fogjuk, a hely-paraméter igazából a várható érték, a skála-paraméter pedig a szórás.) A normális eloszlás talán a legfontosabb eloszlás a valószínűségszámítás és a matematikai statisztika területén. Nagyon széles körben alkalmazzák, például hibával terhelt mérési eredmények modellezésére. A normális eloszlással részletesen a Nevezetes eloszlások című fejezetben foglalkozunk.
Legyen standard normális eloszlású. Határozzuk meg és rajzoljuk le a valószínűségi változó sűrűségfüggvényét!
A valószínűségi változó eloszlását nevezik 1 szabadsági fokú chi-négyzet eloszlásnak. A chi-négyzet eloszlásról részletesen a Nevezetes eloszlások című fejezetben olvashatunk.
Legyen normális eloszlású és paraméterekkel, pedig -től független, normális eloszlású és paraméterekkel. Igazoljuk, hogy szintén normális eloszlású, hely- és skála-paraméterekkel!
Legyenek és független standard normális eloszlású valószínűségi változók. Lássuk be, hogy sűrűségfüggvénye az alábbi függvény, majd rajzoljuk le ezt a függvényt:
A valószínűségi változó eloszlását Augustin Cauchy tiszteletére Cauchy eloszlásnak nevezik. A Cauchy eloszlás a Student féle eloszláscsalád tagja. A Student féle eloszlásokról részletesen a Nevezetes eloszlások fejezetben olvashatunk.
Lássuk be, hogy esetén a valószínűségi változó sűrűségfüggvénye
Természetesen ezt is Cauchy eloszlásnak nevezik, a paramétert pedig skála-paraméternek.
Igazoljuk, hogy ha Cauchy eloszlású skála-paraméterrel, pedig egy -tól független Cauchy eloszlás változó skála-paraméterrel, akkor szintén Cauchy eloszlású, méghozzá skála-paraméterrel. Ezzel ekvivalens állítás, hogy
Az előző feladatban tekintett és változók béta eloszlásúak. A Béta eloszlásokkal részletesen a Nevezetes eloszlások című fejezetben foglalkozunk.