]> Generátorfüggvények
  1. Virtual Laboratories
  2. 3. Várható érték
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6

4. Generátorfüggvények

Mint általában, tekintsünk egy eseménytéren egy véletlen kísérletet és egy valószínűségi mértéket. Egy valószínűségi változó generátorfüggvénye nem más, mint bizonyos transzformáltjának a várható értéke. A legtöbb generátorfüggvényre jellemző a következő négy tulajdonság:

  1. Gyenge feltételek teljesülése esetén a generátorfüggvény meghatározza az eloszlást.
  2. Független valószínűségi változók összegének generátorfüggvénye megegyezik a generátorfüggvényeik szorzatával.
  3. A valószínűségi változó momentumait megkaphatjuk a generátorfüggvényéből deriválással.
  4. Generátorfüggvények sorozatának szokásos (pontonkénti) konvergenciája ekvivalens a megfelelő eloszlások gyenge konvergenciájával.

Az 1. tulajdonság a legfontosabb. Gyakran egy valószínűségi változó eloszlását konkrétan nem tudjuk meghatározni, viszont a generátorfüggvényét igen, és így az eloszlását is azonosítani tudjuk. Az ilyen eljárást nevezik inverziónak. A 2. tulajdonság nagyon hasznos, ha független valószínűségi változók összegének eloszlását akarjuk meghatározni. Emlékezzünk vissza, hogy ha ezt sűrűségfüggvények segítségével szeretnénk meghatározni, akkor a konvolúciót kell alkalmaznunk, ami sokszor bonyolult számolásokhoz vezet. A 3. tulajdonság azért fontos, mert sokszor adódik olyan eset, amikor a momentumokat könnyebb a generátorfüggvény segítségével meghatározni, mint a definíció közvetlen alkalmazásával. Az utolsó tulajdonságot nevezik folytonossági tételnek. Igen gyakran könnyebb a generátorfüggvények konvergenciáját igazolni, mint az eloszlásfüggvényekét.

A valószínűségi generátorfüggvény

Definíció

Legyen X egy értékű valószínűségi változó. Az X változó G valószínűségi generátorfüggvénye a t helyen a következő:

G t t X , feltéve, hogy ez a várható érték véges.

Jelölje f az X valószínűségi súlyfüggvényét, azaz f n X n ,  n .

Igazoljuk, hogy

G t n 0 f n t n .

Tehát G t egy hatványsor t -ben, ahol az együtthatók a súlyfüggvény helyettesítési értékei. Az ilyen esetekben a kombinatorikában is használt megnevezés, hogy G az f függvény generátorfüggvénye. Alapvető tétel az analízisben, hogy minden hatványsor esetén található egy r 0 szám, hogy a hatványsor t r esetén abszolút konvergens, t r esetén pedig divergens. Ezt az r számot nevezik konvergenciasugárnak.

Igazoljuk, hogy G 1 1 , tehát r 1 .

Inverzió

Az analízisből szintén jól ismert, hogy egy hatványsort tagonként lehet deriválni, mint a polinomokat. Továbbá a derivált konvergenciasugara megegyezik az eredeti hatványsor konvergenciasugarával. Jelöljük az n -edik deriváltat n G -nel.

Igazoljuk, hogy f n n G 0 n minden n esetén. Tehát a G valószínűségi generátorfüggvény meghatározza X eloszlását.

Igazoljuk, hogy N  páros   1 G 1 2 .

Momentumok

Legyenek n és k nemnegatív egészek, k n . Ekkor n elemből k darabot

n k n n 1 n k 1 -féleképp választhatunk ki, ha a sorrend is számít. Ezt nevezik ismétlés nélküli variációnak.

Tegyük fel, hogy a konvergenciasugárra r 1 teljesül. Igazoljuk, hogy k G 1 X k minden k esetén. Ezeket nevezik faktoriális momentumoknak. Speciálisan azt kaptuk, hogy X minden momentuma véges.

Igazoljuk, hogy

  1. X G 1 ,
  2. X 2 G 1 G 1 1 G 1 .

Konvolúció

Legyenek X 1 és X 2 független valószínűségi változók G 1 és G 2 valószínűségi generátorfüggvénnyel. Igazoljuk, hogy X 1 X 2 valószínűségi generátorfüggvénye

G t G 1 t G 2 t .

Momentum generáló függvény

Definíció

Legyen X valós értékű valószínűségi változó. Ekkor X momentum generáló függvénye a következő M függvény:

M t t X ,  t .

Vegyük észre, hogy t X 0 majdnem biztosan, így bármely t esetén M t vagy véges vagy .

Legyen X folytonos eloszlású -en f sűrűségfüggvénnyel. Igazoljuk, hogy

M t t t x f x .

Tehát X momentum generáló függvénye nagyon hasonlít az eloszlásának Laplace transzformáltjára. A Laplace transzformáltat Simeon Laplace-ról nevezték el, és igen széles körben használják az alkalmazott matematikában.

Inverzió

A momentum generáló függvényekre vonatkozó inverzió tétel azt állítja, hogy ha M t a 0 egy nyílt környezetében, akkor M meghatározza X eloszlását. Tehát ha két -en értelmezett eloszlás momentum generáló függvénye megegyezik, és véges a nulla egy környezetében, akkor a két eloszlás megegyezik.

Momentumok

Legyen X momentum generáló függvénye M , és M véges a 0 egy környezetében. Ekkor X minden momentuma véges. Igazoljuk a következő formula helyességét (a várható érték és az összegzés a végességre tett feltevés miatt cserélhető fel)!

M t n 0 X n n t n .

Igazoljuk, hogy n M 0 X n minden n esetén. Tehát a momentum generáló függvény 0-ban vett deriváltjai meghatározzák az eloszlás momentumait (innen a momentum generáló elnevezés). A kombinatorikában azt mondanánk, hogy a momentum generáló függvény a momentumok sorozatának exponenciális generátorfüggvénye.

Következésképp, ha egy eloszlásnak valamelyik momentuma végtelen, nem lehet véges a momentum generáló függvénye sem. Viszont az is előfordulhat, hogy a valószínűségi változónk minden momentuma véges, mégsem létezik a momentum generáló függvénye. Nemsokára mutatunk erre példát.

Transzformációk

Legyen X valós értékű valószínűségi változó M momentum generáló függvénnyel, a és b pedig konstansok. Igazoljuk, hogy Y a X b momentum generáló függvénye

N t b t M a t .

Tegyük fel, hogy X 1 és X 2 független, valós értékű valószínűségi változók M 1 és M 2 momentum generáló függvénnyel. Igazoljuk, hogy Y X 1 X 2 momentum generáló függvénye

M t M 1 t M 2 t .

Legyen X egy értékű valószínűségi változó G valószínűségi generátorfüggvénnyel. Igazoljuk, hogy X momentum generáló függvénye

M t G t .

Chernoff korlátok

Legyen X valós értékű valószínűségi változó M momentum generáló függvénnyel. Igazoljuk a Chernoff korlátokat:

  1. X x t x M t ,  t 0 ,
  2. X x t x M t ,  t 0 .

Segítség: Igazoljuk, hogy X x t X t x ha t 0 és X x t X t x ha t 0 , majd használjuk a Markov egyenlőtlenséget.

Természetesen a legjobb Chernoff korlát (akár az (a) akár a (b) esetben) az a t , amelyre a t x M t kifejezés minimális.

Karakterisztikus függvények

Definíció

Matematikus szemmel nézve a leghasznosabb generátorfüggvény a karakterisztikus függvény, mely egy X valós értékű valószínűségi változó esetén a következő függvény:

χ t t X t X t X ,  t .

Mivel χ egy komplex értékű függvény, ezért ezen rész megértéséhez feltételezünk bizonyos szintű komplex függvénytani ismereteket. Vegyük észre, hogy χ jól definiált minden t -re, hisz a valószínűségi változó, melynek a várható értékét vesszük, korlátos. Valóban, t X 1 minden t esetén. A karakterisztikus függvény tulajdonságai elegánsabbak, mint a momentum generáló függvény tulajdonságai, mivel a karakterisztikus függvény mindig létezik.

Tegyük fel, hogy X folytonos eloszlású -en f sűrűségfüggvénnyel. Igazoljuk, hogy

χ t x t x f x .

Tehát X karakterisztikus függvénye megegyezik f Fourier transzformáltjával. A Fourier transzformáltat Joseph Fourier-ről nevezték el, és nagyon sokat használják az alkalmazott matematikában.

Inverzió

A karakterisztikus függvény meghatározza az eloszlást, azaz X és Y pontosan akkor azonos eloszlású valószínűségi változók, ha a karakterisztikus függvényük megegyezik. Valóban, az általános inverziós formula szerint, ha a b , akkor

t n n a t b t 2 t χ t a X b 12 X b X a  ha   n .

A jobb oldalon szereplő valószínűségek pedig egyértelműen meghatározzák X eloszlását. Legyen X folytonos eloszlású, f sűrűségfüggvénnyel. Az inverziós formula speciális esete szerint ekkor minden olyan x pontban, ahol f differenciálható,

f x 1 2 t t x χ t .

Momentumok

Mint a többi generátorfüggvény, a karakterisztikus függvény is alkalmas arra, hogy a segítségével meghatározzuk X momentumait. Sőt, ezt akkor is megtehetjük, ha nem minden momentum véges. Ha X n , akkor

χ t k 0 n X k k t k o t n ,

és így n χ 0 n X n .

Transzformációk

Legyen X valós értékű valószínűségi változó χ karakterisztikus függvénnyel, valamint legyenek a és b konstansok. Igazoljuk, hogy Y a X b karakterisztikus függvénye

ψ t b t χ a t .

Legyenek X 1 és X 2 független, valós értékű valószínűségi változók χ 1 és χ 2 karakterisztikus függvénnyel. Igazoljuk, hogy Y X 1 X 2 karakterisztikus függvénye

χ t χ 1 t χ 2 t .

Egy valószínűségi változó karakterisztikus függvényét megkaphatjuk a momentum generáló függvényéből, ha ez utóbbi létezik. Konkrétan, ha X egy valós értékű valószínűségi változó M momentum generáló függvénnyel, amelyre M t a 0 egy I környezetében, és X karakterisztikus függvényét χ -vel jelöljük, akkor fennáll χ t M t , amint t I .

Eloszlások konvergenciája

Végül a karakterisztikus függvények és az eloszlásban való konvergencia (más néven gyenge konvergencia) kapcsolatát tárgyaljuk. Legyen X 1 X 2 valós értékű valószínűségi változók sorozata, amelyek karakterisztikus függvénye rendre χ 1 χ 2 . A fenti valószínűségi változók nem feltétlen azonos valószínűségi mezőn definiáltak.

A folytonossági tétel szerint ha X n eloszlásban konvergál az X valószínűségi változó eloszlásához, amint n , és X karakterisztikus függvénye χ , akkor χ n t χ t amint n minden t -re. Megfordítva, ha χ n t χ t amint n a 0 egy nyílt környezetében, és χ folytonos a 0-ban, akkor χ egy X valószínűségi változó karakterisztikus függvénye, és X n eloszlásban tart X eloszlásához, amint n .

A folytonossági tétel segítségével igazolható a centrális határeloszlás tétel, a valószínűségszámítás egyik legfontosabb tétele. Továbbá a folytonossági tétel könnyen általánosítható n -en értelmezett eloszlásokra.

Együttes karakterisztikus függvény

Legyen most X Y egy véletlen vektor, amely 2 -en veszi fel az értékeit. Ekkor X Y (együttes) karakterisztikus függvénye:

χ s t s X t Y ,  s t 2 .

Mint az előbb, χ legfontosabb tulajdonsága most is a kölcsönösen egyértelműség: két 2 értékű vektor valószínűségi változónak pontosan akkor egyezik meg a karakterisztikus függvénye, ha megegyezik az eloszlása.

Az együttes momentumok deriválással megkaphatók a karakterisztikus függvényből. Legyen m és n . Ha X m Y n , akkor

m , n χ 0 0 m n X m Y n .

Jelölje ezután χ 1 , χ 2 és χ + rendre az X , Y és X Y valószínűségi változók karakterisztikus függvényét.

Igazoljuk, hogy

  1. χ s 0 χ 1 s ,
  2. χ 0 t χ 2 t ,
  3. χ t t χ + t .

Igazoljuk, hogy X és Y pontosan akkor függetlenek, ha χ s t χ 1 s χ 2 t minden s t vektor esetén.

Természetesen a kétváltozós karakterisztikus függvényekre vonatkozó tételek igazak több változó esetén is, csak a formalizmus bonyolultabb.

Példák, alkalmazások

Bernoulli kísérletek

Legyen X indikátor valószínűségi változó, és X 1 p , ahol p 0 1 paraméter. Igazoljuk, hogy X valószínűségi generátorfüggvénye G t 1 p p t amint t .

A Bernoulli kísérletek folyamata egy X 1 X 2 független, azonos eloszlású indikátor valószínűségi változókból álló sorozat. Megbízhatóság-elméleti kifejezéssel élve X i jelöli az i -edik kísérlet eredményét, ahol 1-et írunk, ha sikeres volt a kísérlet és 0-t, ha sikertelen. A siker valószínűsége p X i 1 , ez a folyamat paramétere. Nevét James Bernoulli-ról kapta. A folyamat részletes tárgyalása a Bernoulli kísérletek fejezetben található.

Az első n kísérlet között a sikeresek száma Y n i 1 n X i . Ez a valószínűségi változó binomiális eloszlású n és p paraméterekkel, és a súlyfüggvénye:

Y n k n k p k 1 p n k ,  k 0 1 n .

Igazoljuk, hogy Y n valószínűségi generátorfüggvénye G n t 1 p p t n ,  t kétféleképpen is:

  1. először a definíció és a súlyfüggvény segítségével,
  2. majd írjuk fel Y n -et független valószínűségi változók összegeként, és használjuk az előző feladat eredményét!

Igazoljuk, hogy

  1. Y n k n k p k ,
  2. Y n n p ,
  3. Y n n p 1 p ,
  4. Y n  páros 12 1 1 2 p n .

Tegyük fel, hogy W valószínűségi súlyfüggvénye N n p 1 p n 1  , n , ahol p 0 1 paraméter. Azaz, W geometriai eloszlású -on p paraméterrel, és az első sikeres kísérletet modellezi egy Bernoulli kísérletsorozatban. Jelölje H W valószínűségi generátorfüggvényét. Igazoljuk, hogy

  1. H t p t 1 1 p t ,  t 1 1 p ,
  2. W k k 1 p k 1 p k ,
  3. W 1 p ,
  4. W 1 p p 2 ,
  5. W  páros 1 p 2 p .

Legyen U binomiális eloszlású m és p paraméterekkel, V pedig szintén binomiális eloszlású n és q paraméterekkel, továbbá legyenek U és V függetlenek.

  1. Határozzuk meg U V valószínűségi generátorfüggvényét!
  2. Igazoljuk, hogy ha p q , akkor U V binomiális eloszlású m n és p paraméterekkel!
  3. Igazoljuk, hogy ha p q , akkor U V nem binomiális eloszlású!

Poisson eloszlás

A Poisson eloszlás súlyfüggvénye

f n a a n n ,  n ,

ahol a 0 paraméter (nevét Simeon Poisson-ról kapta). Gyakran használják egy adott halmazba eső véletlen pontok számának leírására, ekkor nyilván az a paraméter arányos a halmaz méretével. A Poisson eloszlás részletes tárgyalása a Poisson folyamat fejezetben található.

Legyen X Poisson eloszlású a paraméterrel. Jelölje G az X változó valószínűségi generátorfüggvényét. Igazoljuk, hogy

  1. G t a t 1 ,  t ,
  2. X k a k ,
  3. X a ,
  4. X a ,
  5. X  páros 12 1 2 a .

Legyen X Poisson eloszlású a paraméterrel, Y pedig b paraméterű Poisson eloszlású. Legyenek továbbá X és Y függetlenek. Igazoljuk, hogy X Y Poisson eloszlású a b paraméterrel.

Tegyük fel, hogy X Poisson eloszlású a 0 paraméterrel. A Chernoff korlát segítségével igazoljuk, hogy

X n n a a n n ,  n a .

Jelölje G n az n és p n paraméterű binomiális eloszlás valószínűségi generátorfüggvényét, ahol n p n a amint n (és a 0 ). Jelölje G az a paraméterű Poisson eloszlás valószínűségi generátorfüggvényét. Igazoljuk, hogy G n t G t amint n minden t esetén! Tehát az n és p n paraméterű binomiális eloszlás konvergál az a paraméterű Poisson eloszláshoz, amint n .

Exponenciális eloszlás

Az exponenciális eloszlás egy folytonos eloszlás, melynek sűrűségfüggvénye

f t r r t ,  t 0 ,

ahol r 0 egy paraméter, melyet gyakran rátának neveznek. Ez az eloszlás jól modellezi bizonyos gépek, alkatrészek meghibásodásáig eltelt időt, vagy egyes érkezési időpontokat. Az exponenciális eloszlás részletes tárgyalása a Poisson folyamat fejezetben található.

Tegyük fel, hogy X exponenciális eloszlású r paraméterrel. Jelölje M az X változó momentum generáló függvényét. Igazoljuk, hogy

  1. M s r r s ,  s r ,
  2. X n n r n .

Tegyük fel, hogy X X 1 X 2 X n független, azonos, r paraméterű exponenciális eloszlású valószínűségi változók sorozata. Határozzuk meg T i 1 n X i momentum generáló függvényét! A T valószínűségi változó n és r paraméterű gamma eloszlást követ.

Egyenletes eloszlás

Tegyük fel, hogy X egyenletes eloszlású az a b intervallumon. Legyen M az X változó momentum generáló függvénye. Igazoljuk, hogy

  1. M t b t a t b a t t 0 1 t 0 ,
  2. X n b n 1 a n 1 n 1 b a .

Tegyük fel, hogy X Y egyenletes eloszlású a T x y 2 0 x y 1 háromszögön.

  1. Határozzuk meg az X Y pár együttes momentum generáló függvényét!
  2. Határozzuk meg X momentum generáló függvényét!
  3. Határozzuk meg Y momentum generáló függvényét!
  4. Határozzuk meg X Y momentum generáló függvényét!

Legyen az X Y pár együttes sűrűségfüggvénye f x y x y ,  0 x 1 ,  0 y 1 .

  1. Határozzuk meg X Y momentum generáló függvényét!
  2. Határozzuk meg X momentum generáló függvényét!
  3. Határozzuk meg Y momentum generáló függvényét!
  4. Határozzuk meg X Y momentum generáló függvényét!

Normális eloszlás

A standard normális eloszlás egy folytonos eloszlás, melynek sűrűségfüggvénye:

φ z 1 2 12 z 2 ,  z .

A Normális eloszlás rendkívül széles körben alkalmazható, például hibával terhelt mérési eredmények modellezésére. Részletes tárgyalása a Nevezetes eloszlások fejezetben található.

Tegyük fel, hogy Z standard normális eloszlású, és jelölje M a momentum generáló függvényét. Igazoljuk, hogy

  1. M t 12 t 2 ,  t ,
  2. Z 2 n 2 n 2 n n ,  n ,
  3. Z 2 n 1 0 ,  n .

Legyen Z ismét standard normális eloszlású. Ekkor X μ σ Z normális eloszlású μ várható értékkel és σ szórással. Igazoljuk, hogy X momentum generáló függvénye M t μ t 12 σ 2 t 2 amint t !

Tegyük fel, hogy X és Y független, normális eloszlású valószínűségi változók. Igazoljuk, hogy X Y szintén normális eloszlású.

Pareto eloszlás

Tegyük fel, hogy X Pareto eloszlású, ami egy folytonos eloszlás,

f x a x a 1 ,  x 1

sűrűségfüggvénnyel, ahol a 0 paraméter. Az eloszlás Vilfredo Pareto-ról kapta a nevét. Ez egy lassan lecsengő eloszlás, melyet gyakran alkalmaznak különböző pénzügyi mennyiségek (pl. bevétel) modellezésére. A Pareto eloszlást részletesen a Nevezetes eloszlások fejezetben tárgyaljuk.

Legyen M az X változó momentum generáló függvénye. Igazoljuk, hogy

  1. X n a a n n a n a ,
  2. M t bármely t 0 esetén!

Cauchy eloszlás

Tegyük fel, hogy X Cauchy eloszlású, ami egy folytonos eloszlás

f x 1 1 x 2 ,  x

sűrűségfüggvénnyel. Ez az eloszlás nevét Augustin Cauchy-ról kapta, és tagja a Student t eloszláscsaládnak. A t eloszlásokról részletesen a Nevezetes eloszlások fejezetben olvashatunk. Az f függvény gráfját szokás Agnesi boszorkányának nevezni Maria Agnesi tiszteletére.

Legyen M az X változó momentum generáló függvénye. Igazoljuk, hogy

  1. X nem létezik,
  2. M t amint t 0 .

Jelölje χ X karakterisztikus függvényét. Igazoljuk, hogy χ t t amint t !

Ellenpélda

A Pareto eloszlásnál nem minden momentum véges, ezért természetesen a momentum generáló függvény végtelen. Most mutatunk egy példát olyan eloszlásra, ahol az összes momentum véges, mégis végtelen a momentum generáló függvény. Sőt, látni fogunk két különböző eloszlást, melyek összes momentuma megegyezik.

Tegyük fel, hogy Z standard normális eloszlású, és legyen X Z . Ezen X eloszlását lognormális eloszlásnak nevezik.

Változócserével igazoljuk, hogy X sűrűségfüggvénye

f x x 2 2 2 x ,  x 0 .

A standard normális eloszlás momentum generáló függvénye segítségével igazoljuk, hogy X n 12 n 2 , amint n . Tehát X minden momentuma véges.

Igazoljuk, hogy t X amint t 0 . Azaz X momentum generáló függvénye végtelen minden pozitív t helyen.

Legyen most h x 2 x ,  x 0 . Igazoljuk, hogy n esetén

x 0 x n f x h x 12 n 2 2 U ,

ahol U normális eloszlású n várható értékkel és 1 szórással. Segítség: használjuk az u x változócserét, és a kitevőben alkalmazzunk teljes négyzetté alakítást!

Az előző feladat eredményét felhasználva szimmetria érveléssel igazoljuk, hogy n esetén

x 0 x n f x h x 0 .

Legyen g x f x 1 h x ,  x 0 . Az előző feladat eredményét felhasználva igazoljuk, hogy g egy valószínűségeloszlás sűrűségfüggvénye.

Legyen az Y valószínűségi változó sűrűségfüggvénye g . A 40. feladat eredményét felhasználva igazoljuk, hogy Y momentumai megegyeznek X momentumaival. Azaz, Y n 12 n 2 amint n .

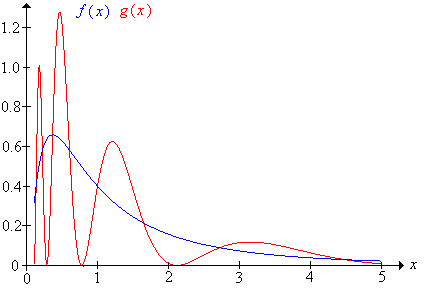
Az f és a g függvény gráfjai láthatók az alábbi ábrán kékkel, illetve pirossal jelölve.

Densities of two distributions with the same moments
  1. Virtual Laboratories
  2. 3. Várható érték
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6