]> Szórásnégyzet és magasabb momentumok
  1. Virtual Laboratories
  2. 3. Várható érték
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6

2. Szórásnégyzet és magasabb momentumok

A bevezetőben említettük, hogy egy valószínűségi változó különböző függvényeinek várható értéke révén a valószínűségi változó sok fontos tulajdonságát jellemezhetjük. Ebben a fejezetben ezzel a módszerrel többek között az eloszlás elkentségét, ferdeségét fogjuk vizsgálni.

Szórásnégyzet

Definíciók

Mint általában, tekintsünk egy eseménytéren egy véletlen kísérletet és egy valószínűségi mértéket. Tegyük fel, hogy X egy S értékű, a kísérlettől függő valószínűségi változó. Emlékezzünk vissza arra, hogy X várható értéke vagy átlaga nem más, mint az eloszlásának középértéke. X szórásnégyzete pedig egy olyan mennyiség, amely azt méri, hogy az eloszlás mennyire elkent a várható érték körül. A formális definíció:

X X X 2 .

A szórásnégyzetet szokás varianciának is nevezni, erre utal a fenti jelölés is. Szerepelt korábban az is, hogy X -nek az a középpontú második momentuma X a 2 . Tehát a szórásnégyzet épp X μ X középpontú második momentuma, vagy más szóval második centrált momentuma. A második momentumnak van egy érdekes fizikai interpretációja. Ehhez képzeljük el, hogy X eloszlása egy tömegeloszlás -en. Ekkor az X a középpontú második momentuma épp a tömegeloszlás a középpontú tehetetlenségi nyomatéka. Intuitívan ez nem más, mint a tömegeloszlás ellenállása az a középpontú forgatásokkal szemben. Speciálisan, X szórásnégyzete épp a μ tömegközéppontú tehetetlenségi nyomaték.

MomentIertial.png

Tegyük fel, hogy X diszkrét eloszlású, és a súlyfüggvénye f . A változócserére vonatkozó tétellel igazoljuk, hogy

X x S x X 2 f x .

Tegyük fel, hogy X folytonos eloszlású, és a sűrűségfüggvénye f . A változócserére vonatkozó tétellel igazoljuk, hogy

X x S x X 2 f x .

Az X változó szórása a szórásnégyzetének gyöke. Ez a mennyiség is az eloszlás elkentségét méri, viszont a mértékegysége ugyanaz, mint X mértékegysége:

𝔻 X X .

Tulajdonságok

A következő feladatok a szórásnégyzet néhány alapvető tulajdonságára világítanak rá. A megoldásuk természetesen a várható érték tulajdonságain múlnak:

Igazoljuk, hogy X X 2 X 2 .

Igazoljuk, hogy X 0 .

Igazoljuk, hogy X 0 pontosan akkor, ha X c 1 valamilyen c konstanssal.

Lássuk be, hogy ha a és b konstansok, akkor a X b a 2 X .

Igazoljuk, hogy az alábbi valószínűségi változónak 0 a várható értéke és 1 a szórásnégyzete:

Z X X 𝔻 X .

A 7. feladatban szereplő Z valószínűségi változót nevezik az X változó standardizáltjának. Mivel X , a várható értéke és a szórása mind azonos mértékegységű mennyiségek, ezért a Z standardizált dimenzió nélküli mennyiség. Ez a mennyiség igazából X -nek az X -től mért előjeles távolsága, a szóráshoz viszonyítva.

Ha X 0 , a szórás és a várható érték hányadosa a variációs együttható. Értelemszerűen ez is dimenziómentes mérőszám.

cv X 𝔻 X X .

Csebisev egyenlőtlenség

A Csebisev egyenlőtlenség (nevét Pafnutyij Csebisev-ről kapta) felső becslést ad annak a valószínűségére, hogy a valószínűségi változó értéke egy bizonyos távolságnál messzebb esik a várható értékétől. Igen hasznos gyakorlati feladatokban, hiszen alkalmazható akkor is, ha nem ismerjük az eloszlást, elég, ha a várható értékre és a szórásnégyzetre van egy jó becslésünk. A következő két feladatban tegyük fel, hogy X egy valós értékű valószínűségi változó μ X várható értékkel és σ 𝔻 X szórással.

A Markov egyenlőtlenség felhasználásával igazoljuk a Csebisev egyenlőtlenséget:

X μ t σ 2 t 2  amint   t 0 .

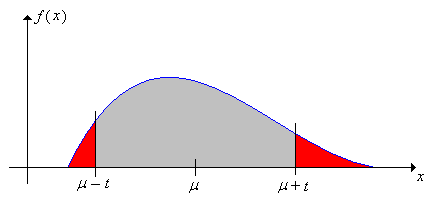
Igazoljuk a Csebisev egyenlőtlenség következő, az előzővel ekvivalens alakját:

X μ k σ 1 k 2  amint   k 0 .

A Csebisev egyenlőtlenség nagy előnye, hogy az eloszlástól függetlenül igaz (feltéve, hogy létezik a várható érték és a szórásnégyzet). Ugyanakkor hátránya, hogy meglehetősen durva becslést ad. Például vegyük észre, hogy az utóbbi feladatban a becslés semmitmondó, ha k 1 , hiszen az 1 felső becslés bármilyen esemény valószínűségére.

Példák és alkalmazások

Indikátor változók

Tegyük fel, hogy X egy indikátor változó, és X 1 p .

  1. Emlékezzünk vissza, hogy már beláttuk, hogy X p .
  2. Igazoljuk, hogy X p 1 p .
  3. Rajzoljuk le a X függvény gráfját, ahol p független változó.

Vegyük észre, hogy X legkisebb értéke 0, melyet a p 0 és a p 1 esetekben vesz fel. A legnagyobb értéke pedig 14 , a p 12 paraméterérték esetén.

Egyenletes eloszlás

Tegyük fel, hogy X diszkrét egyenletes eloszlású az m m 1 n halmazon (ahol m n ).

  1. Emlékezzünk vissza, hogy már beláttuk, hogy X 12 m n .
  2. Igazoljuk, hogy X 112 n m n m 2 .

Tegyük fel, hogy X folytonos egyenletes eloszlású az a b intervallumon.

  1. Emlékezzünk vissza, hogy már beláttuk, hogy X 12 a b .
  2. Igazoljuk, hogy X 112 b a 2 .

Vegyük észre, hogy mind a diszkrét, mind a folytonos esetben a szórásnégyzet csak az intervallum hosszától függ.

Kockadobások

Egy hagyományos kocka alatt hat oldalú dobókockát értünk. Az igazságos kocka olyan, hogy ha feldobjuk, minden oldalára azonos valószínűséggel esik. Az egy-hat irányban lapos kocka egy hagyományos kocka, ami feldobás után az 1 és 6 értékeket 14 , a 2, 3, 4 és 5 értékeket 18 valószínűséggel mutatja.

Egy hagyományos, igazságos kockát feldobtunk. Határozzuk meg a dobott érték várható értékét, szórásnégyzetét és szórását!

A kockadobálós kísérletben válasszunk egy igazságos kockát. Szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és a valódi szóráshoz.

Feldobtunk egy egy-hat irányban lapos kockát. Határozzuk meg a dobott érték várható értékét, szórásnégyzetét és szórását.

A kockadobálós kísérletben válasszunk egy egy-hat irányban lapos kockát. Szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és a valódi szóráshoz.

Poisson eloszlás

A Poisson eloszlás súlyfüggvénye

f n a a n n ,  n ,

ahol a 0 paraméter (nevét Simeon Poisson-ról kapta). Gyakran használják egy adott halmazba eső véletlen pontok számának leírására, ekkor nyilván az a paraméter arányos a halmaz méretével. A Poisson eloszlás részletes tárgyalása a Poisson folyamat fejezetben található.

Tegyük fel, hogy N Poisson eloszlású a paraméterrel.

  1. Emlékezzünk vissza, hogy már beláttuk, hogy N a .
  2. Igazoljuk, hogy N a .

Tehát azt kaptuk, hogy a paraméter az eloszlás várható értéke és szórásnégyzete is egyben.

A Poisson kísérletben a paraméter a r t . Változtassuk a paraméterértéket, és figyeljük meg, hogyan változik az empirikus várható értéket és empirikus szórást jelölő intervallum. Néhány kiválasztott paraméterértékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és a valódi szóráshoz.

Geometriai eloszlás

A geometriai eloszlás egy -en értelmezett eloszlás, melynek súlyfüggvénye

f n p 1 p n 1 ,  n ,

ahol p 0 1 paraméter. A geometriai eloszlás az első sikeres kísérlet sorszáma egy Bernoulli kísérletsorozatban, ahol a siker valószínűsége p .

Tegyük fel, hogy W geometriai eloszlású, és a siker valószínűsége p .

  1. Emlékezzünk vissza, hogy már beláttuk, hogy W 1 p .
  2. Igazoljuk, hogy W 1 p p 2 .

A negatív binomiális kísérletben állítsuk be a k 1 paraméterértéket, hogy visszakapjuk a geometriai eloszlást. Változtassuk p értékét, és figyeljük meg, hogyan változik az empirikus várható értéket és empirikus szórást jelölő intervallum. Néhány kiválasztott p paraméterértékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és a valódi szóráshoz.

Tegyük fel, hogy W geometriai eloszlású p 34 paraméterrel. Számítsuk ki a valódi értékét és a Csebisev egyenlőtlenségből kapott becslését azon esemény valószínűségének, hogy Y -nak a várható értékétől való távolsága nem kisebb, mint a szórásának kétszerese.

Exponenciális eloszlás

Az exponenciális eloszlás egy folytonos eloszlás, melynek sűrűségfüggvénye

f t r r t ,  t 0 ,

ahol r 0 egy paraméter, melyet gyakran rátának neveznek. Ez az eloszlás jól modellezi bizonyos gépek, alkatrészek meghibásodásáig eltelt időt, vagy egyes érkezési időpontokat. Az exponenciális eloszlás részletes tárgyalása a Poisson folyamat fejezetben található.

Tegyük fel, hogy X exponenciális eloszlású r paraméterrel.

  1. Emlékezzünk vissza, hogy már beláttuk, hogy X 1 r .
  2. Igazoljuk, hogy 𝔻 X 1 r .

Tehát azt kaptuk, hogy az exponenciális eloszlás várható értéke és szórása azonos.

A gamma eloszlás kísérletében állítsuk be a k 1 paraméterértéket, hogy megkapjuk az exponenciális eloszlást. Változtassuk az r értékét, és figyeljük meg, hogyan változik az empirikus várható értéket és empirikus szórást jelölő intervallum. Néhány kiválasztott r paraméterértékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és a valódi szóráshoz.

Tegyük fel, hogy X exponenciális eloszlású r 0 paraméterrel. Számítsuk ki a valódi értékét és a Csebisev egyenlőtlenségből kapott becslését azon esemény valószínűségének, hogy X -nek a várható értékétől való távolsága nem kisebb, mint a szórásának k -szorosa.

Pareto eloszlás

A Pareto eloszlás egy folytonos eloszlás, melynek sűrűségfüggvénye

f x a x a 1 ,  x 1 ,

ahol a 0 paraméter. Az eloszlás Vilfredo Pareto-ról kapta a nevét. Ez egy lassan lecsengő eloszlás, melyet gyakran alkalmaznak különböző pénzügyi mennyiségek (pl. bevétel) modellezésére. A Pareto eloszlást részletesen a Nevezetes eloszlások fejezetben tárgyaljuk.

Tegyük fel, hogy X Pareto eloszlású a paraméterrel.

  1. Emlékezzünk vissza, hogy már beláttuk, hogy X a 0 1 a a 1 a 1 .
  2. Igazoljuk, hogy X  nem definiált  a 0 1 a 1 2 a a 1 2 a 2 a 2 .

A valószínűségi változók kísérletében válasszuk ki a Pareto eloszlást. Változtassuk az a értékét, és figyeljük meg, hogyan változik az empirikus várható értéket és empirikus szórást jelölő intervallum. A következő a paraméterértékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és vizsgáljuk meg az empirikus várható érték és szórás viselkedését.

  1. a 1
  2. a 2
  3. a 3

Normális eloszlás

A standard normális eloszlás egy folytonos eloszlás, melynek sűrűségfüggvénye:

φ z 1 2 12 z 2 ,  z .

A Normális eloszlás rendkívül széles körben alkalmazható, például hibával terhelt mérési eredmények modellezésére. Részletes tárgyalása a Nevezetes eloszlások fejezetben található.

Tegyük fel, hogy Z standard normális eloszlású.

  1. Emlékezzünk vissza, hogy már beláttuk, hogy Z 0 .
  2. Igazoljuk, hogy Z 1 . Segítség: Integráljunk parciálisan Z 2 meghatározásához.

Legyen ismét Z standard normális eloszlású és μ , σ 0 . Ekkor X μ σ Z normális eloszlású μ hely- és σ skála-paraméterrel .

  1. Emlékezzünk vissza, hogy már beláttuk, hogy X μ .
  2. Igazoljuk, hogy X σ 2 .

Tehát, ahogy az elnevezés sugallja is, a μ hely-paraméter egyben a várható érték, a σ skála-paraméter pedig a szórás.

A valószínűségi változók kísérletében válasszuk ki a normális eloszlást. Változtassuk a paramétereket, és figyeljük meg, hogyan változik az empirikus várható értéket és empirikus szórást jelölő intervallum. Néhány kiválasztott paraméterértékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és a valódi szóráshoz.

Béta eloszlás

A következő eloszlások a béta eloszlások családjába tartoznak, melyek alkalmazhatók például véletlenszerűen kialakuló arányok modellezésére. A béta eloszlás részletes tárgyalása a Nevezetes eloszlások fejezetben található.

Rajzoljuk le az alábbi sűrűségfüggvényeket, és mindegyiknek határozzuk meg a várható értékét és a szórását.

  1. f x 6 x 1 x ,  0 x 1 ,
  2. f x 12 x 2 1 x ,  0 x 1 ,
  3. f x 12 x 1 x 2 ,  0 x 1 ,
  4. f x 1 x 1 x ,  0 x 1 .

A (d) részfeladatban lévő béta eloszlást nevezik arkusz szinusz eloszlásnak.

Vegyes feladatok

Tegyük fel, hogy X valós értékű valószínűségi változó, továbbá X 5 és X 4 . Határozzuk meg a következő mennyiségeket:

  1. 3 X 2 ,
  2. X 2 .

Tegyük fel, hogy X 1 és X 2 független valós értékű valószínűségi változók, melyekre X i μ i és 𝔻 X i σ i , amint i 1 2 . Igazoljuk, hogy

X 1 X 2 σ 1 2 μ 1 2 σ 2 2 μ 2 2 μ 1 2 μ 2 2 .

Marilyn Vos Savant IQ-ja 228. Tegyük fel, hogy az IQ pontok eloszlásának 100 a várható értéke és 15 a szórása. Határozzuk meg Marilyn intelligencia hányadosának standardizáltját!

Magasabb momentumok

Tegyük fel, hogy X egy valós értékű valószínűségi változó. Az előbb definiált szórásnégyzet nem más, mint X várható értéke körüli második momentuma, ami X eloszlásának a várható értéke körüli elkentségét méri. Ugyanakkor X harmadik és negyedik momentuma is érdekes mennyiségeket mér. A harmadik momentum a ferdeséget méri, azaz, hogy az eloszlás mennyire nem szimmetrikus. A negyedik momentum a lapultságot méri, azaz, hogy mennyire csúcsos az eloszlás. Pontosabban ahhoz, hogy ezeket a mennyiségeket mérjük, a szórás megfelelő hatványával leosztunk, hogy mértékegység nélküli mérőszámot kapjunk. Mint mindig, a következőkben is feltesszük, hogy a megfelelő várható értékek léteznek, és bevezetjük a μ X és a σ 𝔻 X jelöléseket.

Ferdeség

Az X valószínűségi változó ferdesége (vagy ferdeségi együtthatója) a standardizáltjának a harmadik momentuma, azaz:

X X μ σ 3 .

X eloszlását pozitív ferdeségűnek, negatív ferdeségűnek, illetve szimmetrikusnak nevezzük, attól függően, hogy X pozitív, negatív, vagy 0. Durván szólva azt mondhatjuk, hogy ha pozitív a ferdeség, akkor a súly-, vagy sűrűségfüggvénynek lassabb a lecsengése a pozitív irányban. Következésképpen több súly esik a negatív irányba. Analóg módon, ha negatív a ferdeség, akkor a súly-, vagy sűrűségfüggvénynek lassabb a lecsengése a negatív irányban, következésképpen több súly esik a pozitív irányba.

Tegyük fel, hogy X folytonos eloszlású f sűrűségfüggvénnyel, amely szimmetrikus az a pont körül: f a t f a t ,  t .

  1. Lássuk be, hogy X a .
  2. Igazoljuk, hogy X 0 .

Igazoljuk, hogy

X X 3 3 μ X 2 2 μ 3 σ 3 .

Lapultság

Az X valószínűségi változó lapultsága a standardizáltjának negyedik momentuma:

X X μ σ 4 .

Minél nagyobb egy eloszlás lapultsága, annál "hegyesebb a csúcsa" és annál "lassabb a lecsengése".

Igazoljuk, hogy

X X 4 4 μ X 3 6 μ 2 X 2 3 μ 4 σ 4 .

Feladatok

Tegyük fel, hogy X egyenletes eloszlású az a b intervallumon. Határozzuk meg a következő mennyiségeket:

  1. X ,
  2. X .

Tegyük fel, hogy X exponenciális eloszlású r 0 rátával. Határozzuk meg a következő mennyiségeket:

  1. X ,
  2. X .

Tegyük fel, hogy X Pareto eloszlású a 4 paraméterrel. Határozzuk meg a következő mennyiségeket:

  1. X ,
  2. X .

Tegyük fel, hogy Z standard normális eloszlású. Határozzuk meg a következő mennyiségeket:

  1. Z ,
  2. Z .

Rajzoljuk le a következő sűrűségfüggvények gráfját, és minden esetben határozzuk meg a várható értéket, a szórásnégyzetet, a ferdeséget és a lapultságot! (A feladatban szereplő összes eloszlás a béta eloszláscsalád tagja).

  1. f x 6 x 1 x ,  0 x 1 ,
  2. f x 12 x 2 1 x ,  0 x 1 ,
  3. f x 12 x 1 x 2 ,  0 x 1 ,
  4. f x 1 x 1 x ,  0 x 1 , az arkusz szinusz eloszlás.

Alapfogalmak a vektorterek elméletéből

A szórásnégyzet és a magasabb momentumok szoros kapcsolatban állnak a vektorterek norma és távolság fogalmaival. Ha megértjük ezt az összefüggést, jobban átláthatjuk a momentumok jelentését.

Tekintsünk egy V vektorteret, amely az Ω F valószínűségi mezőn értelmezett valós értékű valószínűségi változókból áll (azaz minden valószínűségi változó ugyanattól a véletlen kísérlettől függ). Két valószínűségi változót ekvivalensnek nevezünk, ha 1 valószínűséggel megegyeznek. Két ilyen valószínűségi változóhoz rendeljük ugyanazt a vektort, így precízen a vektorterünk a fenti ekvivalencia reláció szerinti ekvivalencia osztályokból áll. Az összeadás legyen a valószínűségi változók, mint függvények összeadása, a skalárral való szorzás pedig a valószínűségi változó, mint függvény, adott (determinisztikus) számmal való szorzása.

Norma

Legyen X valós értékű valószínűségi változó. Minden k 1 -re definiáljuk a k -normát a következő képlettel:

X k X k 1 k .

Tehát X k valamilyen értelemben X nagyságát méri. A következő feladat az alapvető tulajdonságokra világít rá.

Igazoljuk, hogy X k 0 bármely X -re.

Igazoljuk, hogy X k 0 pontosan akkor, ha X 0 1 (azaz, ha X ekvivalens a 0 valószínűségi változóval).

Igazoljuk, hogy c X k c X k bármely c konstansra.

A következő feladatban a Minkowski egyenlőtlenséget bizonyíthatjuk be (amely a nevét Hermann Minkowski-ról kapta). Ezt az összefüggést háromszög egyenlőtlenségnek is hívják.

Igazoljuk, hogy X Y k X k Y k minden X és Y esetén.

  1. Igazoljuk, hogy S x y 2 x 0 y 0 egy konvex halmaz, és g x y x 1 k y 1 k k konkáv S -en.
  2. Az (a) pont és a Jensen egyenlőtlenség segítségével igazoljuk, hogy ha U és V nemnegatív valószínűségi változók, akkor U 1 k V 1 k k U 1 k V 1 k k .
  3. A (b) pontban helyettesítsünk U X k és V Y k -et.

A 42.-45. Feladatokból következik, hogy azon valószínűségi változók, melyeknek véges a k -adik momentuma, az eredeti V vektorterünk egy alterét alkotják, és a k -norma valóban norma ezen a vektortéren:

V k X V X k .

A következő feladatban a Lyapunov egyenlőtlenséget bizonyíthatjuk (amely nevét Aleksandr Lyapunov-ról kapta). Az egyenlőtlenség azt mutatja, hogy a k -norma növekvő k -ban.

Igazoljuk, hogy ha j k , akkor X j X k .

  1. Igazoljuk, hogy S x x 0 konvex, és g x x k j konvex S -en.
  2. Használjuk az (a) feladat eredményét és a Jensen egyenlőtlenséget, hogy belássuk, hogy ha U nemnegatív valószínűségi változó, akkor U k j U k j .
  3. Helyettesítsünk a (b) feladat eredményébe U X j -et, és igazoljuk az állítást.

A Lyapunov egyenlőtlenség következménye, hogy ha j k és X k -adik momentuma véges, akkor X j -edik momentuma is véges. Tehát V k V j altere.

Tegyük fel, hogy X egyenletes eloszlású a 0 1 intervallumon.

  1. Határozzuk meg X k értékét.
  2. Rajzoljuk le az X k függvény gráfját, ahol k a független változó.
  3. Mennyi k X k ?

Tegyük fel, hogy X sűrűségfüggvénye f x a x a 1 ,  x 1 , ahol a 0 paraméter, azaz X Pareto eloszlású a paraméterrel.

  1. Határozzuk meg X k értékét.
  2. Rajzoljuk le az X k függvény gráfját, ahol k a a független változó.
  3. Mennyi k k a X k ?

Tegyük fel, hogy X Y sűrűségfüggvénye f x y x y ,  0 x 1 ,  0 y 1 . Igazoljuk a Minkowski egyenlőtlenséget ebben a speciális esetben.

Távolság fogalmak

A k -norma, mint minden vektortéren értelmezett norma, használható távolság mérésére: egyszerűen a két vektor különbségének a normája a távolságuk. Tehát definiáljuk a k -távolságot (vagy k -metrikát) két valós értékű valószínűségi változó, X és Y között a következő módon:

d k X Y Y X k Y X k 1 k .

A következő feladatokban bizonyítandó tulajdonságok a analógak a 42.-45. feladatokban bizonyítottakkal (és csak egy kevés új számolás szükséges a megoldásukhoz). Azt látjuk be, hogy a k -metrika valóban metrika.

Igazoljuk, hogy d k X Y 0 tetszőleges X , Y esetén.

Igazoljuk, hogy d k X Y 0 pontosan akkor, ha Y X 1 (azaz ha X és Y ekvivalensek).

Igazoljuk, hogy d k X Y d k X Z d k Z Y bármely X , Y , Z esetén (ez a háromszög egyenlőtlenség).

Tehát a szórás nem más, mint X -nek és a várható értékének 2-távolsága:

𝔻 X d 2 X X X X 2 ,

és a szórásnégyzet ennek a kifejezésnek a négyzete. Általánosabban, X a körüli k -adik momentuma nem más, mint X és a k -távolságának k -adik hatványa. A 2-távolság különösen fontos, hogy miért, azt nemsokára meglátjuk. A fontossága indokolja, hogy külön elnevezést kapjon: ez a átlagos négyzetes távolság.

Újra a középértékről és az elkentségről

Az, hogy mit értünk egy eloszlás középértékén és elkentségén, nagyban függ attól, hogy melyik távolságfogalmat használjuk. Egy X valószínűségi változóra először megkeressük azt a t konstanst, amely a legközelebb van X-hez. Itt persze használnunk kell a választott metrikánkat. Az ilyen t -t az adott metrikára vonatkozó középértéknek nevezhetjük. Az ezen t -vel elért minimális távolság pedig a metrikánkra vonatkozó elkentség mértéke.

Alkalmazzuk a fenti eljárást a 2-távolságra! Ezáltal definiáljuk a átlagos négyzetes hiba gyökét:

d 2 X t X t 2 X t 2 ,  t .

Igazoljuk, hogy d 2 X t akkor minimális, ha t X , és ez a minimális érték épp 𝔻 X .

  1. Vegyük észre, hogy a fenti függvény minimumhelye megegyezik a X t 2 függvény minimumhelyével!
  2. Bontsuk ki az X t 2 zárójeles kifejezést, és tagonként vegyünk várható értéket. Ezáltal t -ben egy másodfokú kifejezést kapunk.
  3. Egyszerű számolással igazoljuk az állítást.

Fizikus megfogalmazással élve az előző feladat eredménye azt mutatja, hogy egy X tömegeloszlás t középpontú tehetetlenségi nyomatéka akkor minimális, ha t μ , azaz a forgatási középpont egybeesik a tömegközépponttal.

A hisztogram applet-ben konstruáljunk az alábbiakban megadott eloszlású diszkrét valószínűségi változókat. Figyeljük meg a várható érték ± szórást jelölő intervallum pozícióját, méretét és az átlagos négyzetes hibafüggvény alakját.

  1. Egyenletes eloszlás,
  2. szimmetrikus, "egycsúcsú" eloszlás,
  3. jobbra ferde "egycsúcsú" eloszlás,
  4. balra ferde "egycsúcsú" eloszlás,
  5. szimmetrikus binomiális eloszlás,
  6. U-alakú eloszlás.

Ezután alkalmazzuk a fenti eljárást az 1-távolságra. Ezáltal definiáljuk az átlagos abszolút hiba függvényt:

d 1 X t X t 1 X t ,  t .

Belátjuk, hogy d 1 X t minimális, ha t az X eloszlás mediánja. A diszkrét esetet tárgyaljuk először, egyrészt mert könnyebb, másrészt mert különösen fontos.

Tegyük fel, hogy X egy véges S halmazban veszi fel a helyettesítési értékeit.

  1. Igazoljuk, hogy X t t X X t X t X t .
  2. Igazoljuk, hogy X t a t t b t , ahol a t 2 X t 1 és b t X 2 X X t .
  3. Lássuk be, hogy X t folytonos, szakaszonként lineáris függvény t -ben, melynek töréspontjai S -be esnek. Tehát ez a függvény egy elsőfokú spline.
  4. Legyen m X legkisebb mediánja. Igazoljuk, hogy ha t m és t S , akkor a t -beli lineáris rész meredeksége negatív.
  5. Legyen M X legnagyobb mediánja. Igazoljuk, hogy ha t M és t S , akkor a t -beli lineáris rész meredeksége pozitív.
  6. Lássuk be, hogy ha t m M akkor a t -beli lineáris rész meredeksége 0.
  7. Következtessünk arra, hogy X t minimális minden olyan t -re, amely beleesik az m M mediánintervallumba.

Az legutóbbi feladat rávilágít az átlagos abszolút hiba függvény lényeges hátrányaira:

Valóban, ha X mediánja nem egyértelmű, nincs okunk arra, hogy valamelyik medián értéket a többitől megkülönböztetve az eloszlás közepének tekintsük.

A hisztogram applet-ben konstruáljunk az alábbiakban megadott eloszlású diszkrét valószínűségi változókat. Figyeljük meg a várható értéket és a szórást jelölő intervallum pozícióját, méretét és az átlagos abszolút hibafüggvény alakját.

  1. Egyenletes eloszlás,
  2. szimmetrikus, "egycsúcsú" eloszlás,
  3. jobbra ferde "egycsúcsú" eloszlás,
  4. balra ferde "egycsúcsú" eloszlás,
  5. szimmetrikus binomiális eloszlás,
  6. U-alakú eloszlás.

Legyen X indikátor valószínűségi változó, és X 1 p . Vázoljuk a d 1 X t X t -et, mint t függvényét az alábbi esetekben. Keressük meg a függvény minimumhelyét és minimum értékét!

  1. p 12
  2. p 12
  3. p 12

Legyen most X tetszőleges valós értékű eloszlás. Igazoljuk, hogy d 1 X t pontosan akkor minimális, ha t az X eloszlás mediánja.

  1. Tegyük fel, hogy s t . Számítsunk várható értékeket az alábbi feltételek mellett: X s , s X t , és X t , majd átrendezések segítségével igazoljuk, hogy X t X s t s 2 X s 1 2 t X s X t .
  2. Tegyük fel, hogy t s . Az (a) részfeladathoz hasonlóan igazoljuk, hogy X t X s t s 2 X s 1 2 X t t X s .
  3. Vegyük észre, hogy az (a) és (b) feladatokban szereplő egyenletek jobb oldalainak utolsó tagjai nem negatívak. Ha s -et X mediánjának választjuk meg, akkor a középső tagok sem lehetnek negatívak.
  4. Következtessünk arra, hogy ha s az X eloszlás mediánja, t pedig tetszőleges szám, akkor X t X s .

Konvergencia

Ha van egy távolságfogalmunk, akkor konvergenciát is tudunk definiálni. Legyenek X n ,  n 1 2 és X azonos valószínűségi mezőn definiált valós értékű valószínűségi változók (azaz ugyanattól a véletlen kísérlettől függenek). Azt mondjuk, hogy X n X k középben amint n , ha

d k X n X 0  amint   n , vagy ami ezzel ekvivalens: X n X k 0  amint   n .

A k 1 esetben azt mondjuk, hogy X n X amint n átlagban; k 2 pedig azt mondjuk, hogy X n X amint n négyzetes középben. Ezek a legfontosabb speciális esetek.

A Lyapunov egyenlőtlenség segítségével igazoljuk, hogy ha j k , akkor ha X n X amint n k középben, akkor X n X amint n j középben is.

A következő feladatokban azt igazoljuk, hogy az átlagban való konvergencia erősebb, mint a valószínűségben való konvergencia.

A Markov egyenlőtlenség segítségével igazoljuk, hogy ha X n X amint n átlagban, akkor X n X amint n valószínűségben.

Az állítás megfordítottja nem igaz. Sőt, a majdnem biztos konvergenciából sem következik a k középben való konvergencia, és megfordítva, a k középben való konvergenciából nem következik a majdnem biztos konvergencia. A következő két feladatban ezekre adunk ellenpéldát.

Tegyük fel, hogy X 1 X 2 független valószínűségi változók, hogy

X n n 3 1 n 2 ,  X n 0 1 1 n 2 ,  n .
  1. A Borel-Cantelli lemma első felével igazoljuk, hogy X n 0> amint n majdnem biztosan.
  2. Igazoljuk, hogy X n 0>  amint n valószínűségben.
  3. Igazoljuk, hogy X n amint n .

Tegyük fel, hogy X 1 X 2 független indikátor valószínűségi változók sorozata, továbbá

X n 1 1 n ,  X n 0 1 1 n ,  n .
  1. A Borel-Cantelli lemma második részének segítségével igazoljuk, hogy X n 0  végtelen sok   n  esetén  1 .
  2. A Borel-Cantelli lemma második részének segítségével igazoljuk, hogy X n 1  végtelen sok   n  esetén  1 .
  3. Igazoljuk, hogy X n  nem konvergál, amint   n 1 .
  4. Igazoljuk, hogy X n 0 amint n k -középben minden k 1 esetén.

Az alábbiakban összefoglaljuk, hogy milyen konvergencia típusok implikálják egymást. Semmilyen itt nem szereplő implikáció nem igaz általában.

Kapcsolódó témák

Egy hasonló statisztikai téma a Minta szórásnégyzete rész a Véletlen minták fejezetben. Valószínűségi változók összegének szórásnégyzeténél alapfogalom a kovariancia, amit részleteiben a következő részben tárgyalunk.

  1. Virtual Laboratories
  2. 3. Várható érték
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6