Equivalence Relations

on a nonempty set

S

that is reflexive, symmetric, and transitive is said to be an equivalence relation on

S

. As the name and notation suggest, an equivalence relation is intended to define a type of equivalence among the elements of

S

. Like partial orders, equivalence relations occur naturally in most areas of mathematics, including probability. The equivalence class of an element

x S

is the set of all elements that are equivalent to

x

The most important result is that an equivalence relation on a set

S

defines a partition of

S

Suppose that is an equivalence relation on a set $S$ .

Show that for every $x$ and $y$ in $S$ , $x y$ if $x y$ and $x y$ otherwise.
Show that $x S x > S$ .

Sometimes the set

S

of equivalence classes is denoted

S

. The idea is that the equivalence classes are new objects obtained by identifying elements in

S

that are equivalent. Conversely, every partition of a set defines an equivalence relation on the set.

Suppose that $S$ is a collection of non-empty sets that partition a given set $S$ . Show that the relation defined below is an equivalence relation on $S$ :

x y if and only if x A and y A for some A A

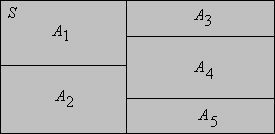
Sometimes the equivalence relation

associated with a given partition

S

is denoted

S S

The process of forming a partition associated with an equivalence relation, and the process of forming an equivalence relation associated with a partition are inverses of each other.

Show that if we start with an equivalence relation on $S$ , form the associated partition, and then construct the equivalence relation associated with the partition, then we end up with the original equivalence relation. In modular notation, $S S$
Show that if we start with a partition of $S$ , form the associated equivalence relation, and then form the partition associated with the equivalence relation, then we end up with the original partition. In modular notation, $S S S S$

Suppose that $S$ is a nonempty set.

Show that equality (=) is an equivalence relation on $S$ and that $x x$ for each $x S$
The trivial relation on $S$ is defined by $x y$ for all $x$ and $y$ in $S$ . Show that is an equivalence relation on $S$ with only one equivalence class, namely $S$ itself.

Every function

f

defines an equivalence relation on its domain, known as the equivalence relation associated with

f

. Moreover, the equivalence classes have a simple description in terms of the inverse images of

f

Suppose that $f S T$ . Define a relation on $S$ by $x y$ if and only if $f x f y$ .

Show that is an equivalence relation on $S$ .
Show that the set of equivalences classes is $S f y y range f$ .
Define the function $F$ from $S$ into $T$ by $F x f x$ . Show that $F$ is well-defined and is one-to-one.

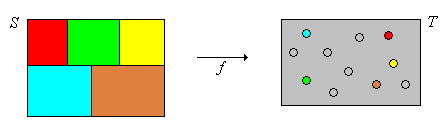
Suppose again that $f S T$ .

If $f$ is one-to-one, show that the equivalence relation associated with $f$ is the equality relation, and hence $x x$ for each $x S$
If $f$ is a constant function, show that the equivalence relation associated with $f$ is the trivial relation, and hence $S$ is the only equivalence class.

Give the equivalence classes explicitly for the functions from into defined below:

$f x x 2$ .
$g x x$ .
$h x x$ .

Suppose that $I$ is a fixed interval of , and that $S$ is the set of differentiable functions from $I$ into . Consider the equivalence relation associated with the derivative operator $D$ on $S$ . For $f S$ , give a simple description of $f$ .

Let $d$ be a positive integer. Define the relation $d$ on by $d m n$ if and only if $d n m$ .

Show that $d$ is an equivalence relation.
Show that the set of distinct equivalence classes is $Z d k n d n k 01 d 1$ .
Let $r$ denote the function on where $r n$ is the remainder when $n$ is divided by $d$ . Show that $d$ is the equivalence relation associated with the function $r$ .

The equivalence relation $d$ is known as congruence modulo $d$ .

Equivalence relations associated with functions are universal: every equivalence relation is of this form:

Suppose that is an equivalence relation on a set $S$ . Define $f S S$ by $f x x$ . Show that is the equivalence relation associated with $f$ .

Suppose that and are equivalence relations on a set $S$ . Let denote the intersection of and (thought of as subsets of $S S$ ). Equivalently, $x y$ if and only if $x y$ and $x y$ . Show that

is an equivalence relation on $S$ .
$x x x$ .

Suppose that we have a relation that is reflexive and transitive, but fails to be a partial order because it's not anti-symmetric. The relation and its inverse naturally lead to an equivalence relation, and then in turn, the original relation defines a true partial order on the equivalence classes. This is a common construction. The details are given in the next exercise.

Suppose that is a relation on a set $S$ that is reflexive and transitive.

Define the relation on S by $x y$ if and only if $x y$ and $y x$ . Show that is an equivalence relation on $S$ .
Suppose that $A$ and $B$ are equivalence classes. Show that if $x y$ for some $x A$ and $y B$ , then $u v$ for all $u A$ and $v B$ .
Now define a relation on the collection of equivalence classes $S$ by $A B$ if and only if $x y$ for some (and hence all) $x A$ and $y B$ . Show that is a partial order on $S$ .

Suppose that $S$ and $T$ are sets and that $T$ is a partial order on $T$ . Suppose also that $f S T$ . Define the relation $S$ on $S$ by $S x y$ if and only if $T f x f y$ . Show that $S$ is reflexive and transitive. The equivalence relation on $S$ constructed in the previous exercise is the equivalence relation associated with the function $f$ . Hence the relation $≼ S$ can be extended to a partial order on the equivalence classes corresponding to $f$ .

Examples from Linear Algebra

Linear algebra provides several examples of important and interesting equivalence relations. To set the stage, let

m n

denote the set of

m n

matrices with real entries.

Row operations are essential for inverting matrices and solving systems of linear equations. If

A

and

B

are

m n

matrices, then

A

and

B

are said to be row equivalent if

A

can be transformed into

B

by a finite sequence of row operations.

Show that row equivalence is an equivalence relation on $m n$ . Hint: Note that each row operation can be reversed by another row operation.

Next recall that

n n

matrices

A

and

B

are said to be similar if there exists an invertible

n n

matrix

P

such that

P A P B

. Similarity is very important in the study of linear transformations, change of basis, and the theory of eigenvalues and eigenvectors.

Show that similarity is an equivalence relation on $n n$ .

Applications to Number Systems

Equivalence relations play an important role in the construction of complex mathematical structures from simpler ones. Often the objects in the new structure are equivalence classes of objects constructed from the simpler structures, modulo an equivalence relation that captures the essential properties of equality for the new objects.

The construction of number systems is a prime example of this general idea. The next exercise explores the construction of rational numbers from integers.

Define a relation on by $j k m n$ if and only if $j n k m$ .

Show that is an equivalence relation.
Now define $m n$ to be the equivalence class generated by $m n$ . Show that this definition agrees with the usual notion of equality of rational numbers.
Show that the usual definitions for addition and multiplication of rational numbers are consistent. That is, these definitions are independent of the particular representatives used for the equivalence classes.

5. Equivalence Relations

Examples from Linear Algebra

Applications to Number Systems