Functions play a central role in probability and statistics, as they do in every other branch of mathematics.

Definitions and Properties

Suppose that and are sets. Technically, a function from into is a subset of the product set with the property that for each element , there exists a unique element such that . We then write . Less formally, a function from into is a rule (or procedure or algorithm) that assigns to each a unique element . The definition of a function as a set of ordered pairs, is due to Kazamierz Kuratowski. When is a function from into , we write

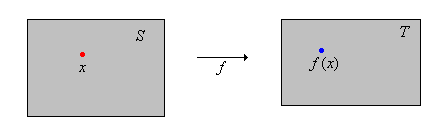
The set is the domain of and the set is the range space or co-domain of . The actual range of is the set of function values:

If the range of is , then is said to map onto (instead of just into). Thus, if maps onto , then for each there exists such that . By definition, any function maps its domain onto its range.

A function is said to be one-to-one if distinct elements in the domain are mapped to distinct elements in the range.

If is a one-to-one function from onto , we can define the inverse of as the function from onto given by

If you like to think of a function as a set of ordered pairs, then . The fact that is one-to-one and onto ensures that is a valid function from onto . Sets and are in one-to-one correspondence if there exists a one-to-one function from onto ; one-to-one correspondence plays an essential role in the study of cardinality.

Composition

Suppose that and . The composition of with is the function defined by

Thus we can write without ambiguity.

The identity function on a set is the function from onto defined by

An element can be thought of as a function from into . Similarly, an element can be thought of as a function from into . For such a sequence , of course, we usually write instead of . More generally, if and are sets, then the set of all functions from into is denoted by .

Inverse Images

Suppose that is a function from a set into a set . If , the inverse image of under is the subset of consisting of those elements that map into :

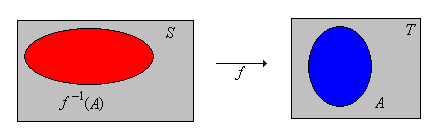
Technically, the inverse images define a new function from into . We use the same notation as for the inverse function, which is defined when is one-to-one and onto. Usually, no confusion results. The following important exercise shows that inverse images preserve all set operations.

The result in part (a) hold for arbitrary unions, and the results in part (b) hold for arbitrary intersections. No new ideas are involved; only the notation is more complicated.

Forward Images

Suppose again that is a function from a set into a set . If , the forward image of under is the subset of given by

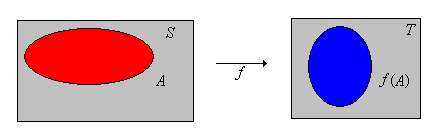
Technically, the forward images define a new function from into , but we use the same symbol for this new function as for the underlying function from into that we started with. Usually, no confusion results.

It might seem that forward images are more natural than inverse images, but in fact, the inverse images are much more important than the forward ones (at least in probability and measure theory). Fortunately, the inverse images are nicer as well--unlike the inverse images, the forward images do not preserve all of the set operations.

The result in part (a) hold for arbitrary unions, and the results in part (b) hold for arbitrary intersections. No new ideas are involved; only the notation is more complicated.

Suppose again that , As noted earlier, the forward images of define a function from into and the inverse images define a function from into One might hope that these functions are inverses of one-another, but alas no.

Indicator Functions

Suppose that is a subset of a universal set . The indicator function of is the function defined as follows:

Thus, there is a one-to-one correspondence between , the power set of , and the collection of indicator functions . The next exercise shows how the set algebra of subsets corresponds to the arithmetic algebra of the indicator functions.

The results in part (a) extends to arbitrary intersections and the results in part (b) extends to arbitrary unions.

Functions into Product Spaces

Suppose that and are sets and that where . For , we define the coordinate function by the rule that is the coordinate of for each . Conversely, a sequence of functions , each mapping into , defines a function by the rule for .

Operations

Suppose that is a set. A function is sometimes called an unary operation on . As the name suggests, operates on an element to produce a new element . Similarly, a function is sometimes called an binary operation on . As the name suggests, operates on a pair of elements to produce a new element .

The arithmetic operations are quintessential examples:

• is a unary operation on
• is a binary operation on
• is a binary operation on
• is a binary operation on
• is a unary operation on

The set operations on were studied in the section on Sets:

• is a unary operation.
• is a binary operation.
• is a binary operation.
• is a binary operation.

Suppose now that is a unary operation on , is a binary operation on , and that . Then is said to be closed under if . Thus, restricted to is a unary operation on . Similarly, is said to be closed under if . Thus, restricted to is a binary operation on . Returning to our basic examples, note that

• is closed under plus and times, but not under minus and difference.
• is closed under plus, times, minus, and difference.

Many properties that you are familiar with for special operations (such as the arithmetic and set operations) can now be formulated generally. Suppose that and are binary operations on . In the following definitions, , , and are arbitrary elements of .

• is commutative if
• is associative if
• distributes over (on the left) if

The Axiom of Choice

Suppose that is a collection of nonempty subsets of a set . The axiom of choice states that there exists a function with the property that for each . The function is known as a choice function.

Stripped of most of the mathematical jargon, the idea is very simple. Since each set is nonempty, we can select an element of ; we will call the element we select and thus our selections define a function. In fact, you may wonder why we need an axiom at all. The problem is that we have not given a rule (or procedure or algorithm) for selecting the elements of the sets in the collection. Indeed, we may not know enough about the sets in the collection to define a specific rule, so in such a case, the axiom of choice simply guarantees the existence of a choice function. Some mathematicians, known as constructionists do not accept the axiom of choice, and insist on well defined rules for constructing functions.

A nice consequence of the axiom of choice is a type of duality between one-to-one functions and onto functions.

Computational Exercises

Some Elementary Functions

Each of the following rules defines a function from into .

Dice

Let . This is the set of possible outcomes when a pair of standard dice are thrown. Let , , and be the functions from into defined by the following rules: