Partial Orders

A relation

S

that is reflexive, anti-symmetric, and transitive is said to be a partial order on

S

. As the name and notation suggest, a partial order is a type of ordering of the elements of

S

. Partial orders occur naturally in many areas of mathematics, including probability.

A partial order

on a set

S

naturally gives rise to several other relations on

S

, and

Show that the inverse of a partial order is also a partial order.

Show that if is a partial order on $S$ and $A$ is a subset of $S$ , then the restriction of to $A$ is a partial order on $A$ .

A partial order

S

is a total order or linear order if it satisfies the additional property that for every

x S

and

y S

, either

x y

y x

. Of course, the ordinary order

is a total order on the set of real numbers

Suppose that $S$ is a set. Show that the subset relation is a partial order on $S$ , the power set of $S$ .

Let $S$ be a set. Show that is a partial order on $S$ if and only if is transitive and irreflexive.

Sub-orders

Suppose that

1

and

2

are partial orders on a nonempty set

S

. Then

1

is an sub-order of

2

, or equivalently

2

is an extension of

1

if and only if

Let denote the division relation on the set of positive integers . That is, $m n$ if and only if there exists $k$ such that $n k m$ . Show that is a partial order on , and is a sub-order of the ordinary order .

Hasse Diagrams

Suppose that

is a partial order on a set

S

. For

x S

and

y S

y

is said to cover

x

x y

but no element

z S

satisfies

x z y

. If

S

is finite, the covering relation completely determines the partial order. Moreover, the covering graph or Hasse graph is the directed graph with vertes set

S

and directed edge set

E

, where

x y E

if and only if

y

covers

x

. Thus,

x y

if and only if there is a directed path in the graph from

x

y

. Hasse graphs are named for the German mathematician Helmut Hasse. The graphs are often drawn with the edges directed upward. In this way, the directions can be inferred without having to actually draw arrows.

Let $S 234612$ .

Sketch the Hasse graph corresponding to the ordinary order on $S$ .
Sketch the Hasse graph corresponding to the division partial order on $S$ .

Orders on Product Spaces

Suppose that $S$ and $T$ are sets with partial orders $S$ and $T$ respectively. Define the relation on $S T$ by $x y z w$ if and only if $S x z$ and $T y w$

Show that is a partial order on $S T$ , called, appropriately enough, the product order.
Suppose that $S S T T$ . Show that if $S$ has at least 2 elements, then is not a total order on $S 2$ .

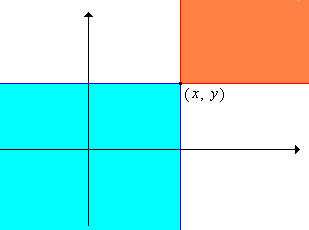
The picture below shows a point

x y 2

. Suppose that

2

is given the product order associated with the ordinary order

. Then the region shaded red is the set of points larger than

x y

The region shaded blue is the set of points smaller than

x y

. The region shaded white is the set of points that are not comparable with

x y

Suppose again that $S$ and $T$ are sets with partial orders $S$ and $T$ respectively. Define the relation on $S T$ by $x y z w$ if and only if either $S x z$ , or $x z$ and $T y w$

Show that is a partial order on $S T$ , called the lexicographic order or dictionary order.
Show that if $S$ and $T$ are total orders on $S$ and $T$ , respectively, then is a total order on $S T$ .

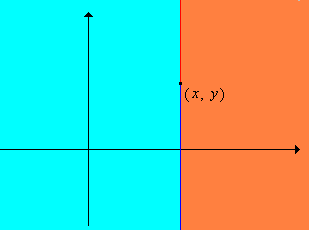
The picture below shows a point

x y 2

. Suppose that

2

is given the lexicographic order associated with the ordinary order

. Then the region shaded red is the set of points larger than

x y

The region shaded blue is the set of points smaller than

x y

Lexicographic orders are not as obscure as you might think. Many standard partially ordered sets can be expressed as lexicographic products.

A real number $x$ can be uniquely expressed in terms of its integer part and remainder:

x n t

where $n x$ and $t x n x x$ . In this way, can be associated with the product space $01$ . Show that corresponds to the lexicographic product of with $01$ , where of course is the ordinary order for real numbers.

Monotone Sets and Functions

Partial orders form a natural setting for increasing and decreasing sets and functions. Suppose first that

is a partial order on a set

S

and that

A S

. Then

Suppose now

S

is a set with partial order

S

and that

T

is another set with partial order

T

. Finally suppose that

f S T

. Then

Suppose that is a partial order on a set $S$ and that $A S$ . Recall the definition of the indicator function $A$ associated with $A$ . Show that

$A$ is increasing if and only if $A$ is increasing.
$A$ is decreasing if and only if $A$ is decreasing.

In a sense, the subset partial order is universal--every partially ordered set is isomorphic to

S

for some collection of sets

S

Suppose that is a partial order on a set $S$ . For each $x S$ , let $A x u S u x$ , and then let $S A x x S$ , so that $S S$ . Show that the function $A S S$ is one-to-one (and of course onto) and satisfies

x y if and only if A x A y

Extremal Elements

Suppose again that

is a partial order on a set

S

and that

A S

. Various types of extremal elements of

A

play important roles.

Show that the minimum and maximum elements of $A$ , if they exist, are unique. They are denoted $min A$ and $max A$ , respectively.

Minimal, maximal, minimum, and maximum elements of a set must belong to that set. The following definitions relate to upper and lower bounds of a set, which do not have to belong to the set.

By the Exercise 10, the greatest lower bound of

A

is unique, if it exists. It is denoted

glb A

inf A

. Similarly, the least upper bound of

A

is unique, if it exists, and is denoted

lub A

sup A

Consider the ordinary order ≤ on the set of real numbers , and let $A a b$ where $a b$ . Find each of the following that exist:

The set of minimal elements of $A$
The set of maximal elements of $A$
$min A$
$max A$
The set of lower bounds of $A$
The set of upper bounds of $A$
$inf A$
$sup A$

Consider the division partial order on the set of positive integers and let $A$ be a non-empty subset of .

Show that if $A$ is infnite then $sup A$ does not exist. If $A$ is finite then $sup A$ is the least common multiple of $A$ , usually denoted $lcm A$ in this context.
Show that $inf A$ is the greatest common divisor of $A$ , usually denoted $gcd A$ in this context.

Again consider the division partial order on the set of positive integers and let $A 234612$ . Find each of the following that exist:

The set of minimal elements of $A$
The set of maximal elements of $A$
$min A$
$max A$
The set of lower bounds of $A$
The set of upper bounds of $A$
$inf A$
$sup A$

Let $S$ be a set and consider the subset partial order on $S$ , the power set of $S$ . Let $A$ be a non-empty subset of $S$ , that is, a non-empty collection of subsets of $S$ . Show that

$inf A A$
$sup A A$

Suppose that

S

is a set and that

f S S

. An element

z S

is said to be a fixed point of

f

f z z

. The following exercise explores a basic fixed point theorem for a partially ordered set. The theorem is important in the study of cardinality.

Suppose that is a partial order on a set $S$ with the property that $sup A$ exists for every $A S$ . If $f$ is an increasing function from $S$ into $S$ , then $f$ has a fixed point. The following steps outline the proof:

Let $A x S x f x$ and let $z sup A$
If $x A$ then $x z$ so $x f x f z$ ,
From (b), $f z$ is an upper bound of $A$ so $z f z$
But then $f z f f z$ so $f z A$
Hence $f z z$
Finally conclude that $f z z$

Limits of Sequences of Real Numbers

Show that $a n a n 1$ is increasing in $n$

The limit of the sequence in the last exercise is the limit inferior of the original sequence:

Show that ^{a
n

a

n
1

is decreasing in
$n$}

The limit of the sequence in the last exercise is the limit superior of the original sequence:

4. Partial Orders

Sub-orders

Hasse Diagrams

Orders on Product Spaces

Monotone Sets and Functions

Extremal Elements

Limits of Sequences of Real Numbers