Poincaré's quote, on the title page of this chapter could not be more wrong (what was he thinking?). Set theory is the foundation of probability and statistics, as it is for almost every branch of mathematics.
First, a set is simply a collection of objects; the objects are referred to as elements of the set. The statement that is an element of set is written . By definition, a set is completely determined by its elements; thus sets and are equal if they have the same elements:
If and are sets then is a subset of if every element of is also an element of :
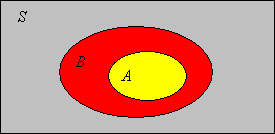
Concepts in set theory are often illustrated with small, schematic sketches known as Venn diagrams, named for John Venn. The Venn diagram in the picture below illustrates the subset relation.
Membership is a primitive, undefined concept in naive set theory. Moreover, sets are usually constructed by either listing the elements of the set or by giving a condition that must be satisfied by the elements of the set. However, the following construction, known as Russell's paradox after the mathematician and philosopher Bertrand Russell, shows that we cannot be too cavalier in the construction of sets.
Let . Show that if and only if
Usually, the sets under discussion in a particular context are all subsets of a specified set , often called a universal set. The use of a universal set prevents the type of problem that arises in Russell's paradox. That is, if is a given set and is a predicate on (that is, a valid mathematical statement that is either true or false for each , then is a valid subset of .
In contrast to a universal set, the empty set, denoted , is the set with no elements.
Show that for every set .
Suppose that , and are subsets of a set . Prove the following results, which show that the subset relation is a partial order on the collection of subsets of .
If is a set, then the set of all subsets of is known as the power set of and is denoted .
The following special sets are used throughout the project, and often play the role of universal sets.
We are now ready to review the basic operations of set theory. For the following definitions, suppose that and are subsets of a universal set, which we will denote by .
The union of and is the set obtained by combining the elements of and .
The intersection of and is the set of elements common to both and :
If the intersection of sets and is empty, then and are said to be disjoint:
The set difference of and is the set of elements that are in but not in :
The complement of is the set of elements that are not in :
Note that union, intersection, and difference are binary set operations, while complement is a unary set operation.
In the Venn diagram applet, select each of the following and note the shaded area in the diagram.
In the following problems, , , and are subsets of a universal set . The proofs are straightforward, and just use the definitions and basic logic.
Show that
Prove the identity laws:
Prove the idempotent laws:
Prove the complement laws:
Prove the double complement law:
Prove the commutative laws:
Prove the associative laws:
Thus, we can write and without ambiguity.
Prove the distributive laws:
Prove DeMorgan's laws (named after Agustus DeMorgan):
Prove that the following statements are equivalent:
Prove the following results. The first part shows that set difference can be expressed in terms of complement and intersection. The next three parts show that all of the other set operations (complement, union, and intersection) can be expressed in terms of difference.
Show that . This set is called the symmetric difference of and , and is sometimes denoted . The elements of this set belong to one but not both of the given sets.
Show that the elements of belong to both the given sets or to neither of the sets.
Prove that there are 16 different (in general) sets that can be constructed from two given events and .
In the Venn diagram applet, observe the diagram of each of the 16 sets that can be constructed from and using the set operations.
Product sets are sets of sequences. The defining property of a sequence, of course, is that order as well as membership is important.
Let us start with ordered pairs. In this case, the defining property is that if and only if and . Interestingly, the structure of an ordered pair can be defined just using set theory. The construction in the exercise below is due to Kazamierz Kuratowski
Define Show that this definition captures the defining property of an ordered pair given above.
More generally, two ordered sequences of the same size (finite or infinite) are the same if and only if their corresponding coordinates agree:
Suppose now that we have a sequence of sets . The Cartesian product of the sets (named for René Descartes) is defined as follows:
If for each , then the product set can be written compactly as . In particular, recall that denotes the set of real numbers so that is -dimensional Euclidean space, named after Euclid, of course.
Finally, suppose that we have an infinite sequence of sets . The Cartesian product of the sets is defined by
The elements of are called bit strings of length . As the name suggests, we sometimes represent elements of this product set as strings rather than sequences (that is, we omit the parentheses and commas). Since the coordinates just take two values, there is no risk of confusion.
We will now see how the set operations relate to the Cartesian product operation. Suppose that and are sets and that , and , . The sets in the exercises below are subsets of
The most important rules that relate Cartesian product with union, intersection, and difference are the distributive rules. Show that
Show that
In general, the product of unions is larger than the corresponding union of products.
On the other hand, the product of intersections is the same as the corresponding intersection of products. Show that
In general, the product of differences is smaller than the corresponding difference of products. Show that
The operations of union and intersection can easily be extended to a finite or even an infinite collection of sets.
Suppose that is a nonempty collection of subsets of a universal set . In some cases, the subsets in may be naturally indexed by a nonempty index set , so that . (In a technical sense, any collection of subsets can be indexed--by itself!)
The union of the collection of sets is the set obtained by combining the elements of the sets in :
If , so that the collection of sets is indexed, then we use the more natural notation:
The intersection of the collection of sets is the set of elements common to all of the sets in :
If , so that the collection of sets is indexed, then we use the more natural notation:
The collection of sets is pairwise disjoint if the intersection of any two sets in the collection is empty:
The collection of sets is said to partition a set if the collection is pairwise disjoint and . Partitions are intimately related to equivalence relations.
In the following problems, is a collection of subsets of a universal set , indexed by a nonempty set , and is a subset of .
Prove the general distributive laws
Then restate the laws in the notation where the collection is not indexed.
Prove the general De Morgan's laws:
Restate the laws in the notation where the collection is not indexed.
Suppose that the collection partitions . Show that for any subset , the collection partitions .
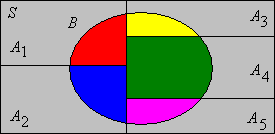
Let . This is the set of outcomes when a 4-sided die and a 6-sided die are tossed. Further let and . Give each of the following sets in list form:
Let . This is the set of outcomes when a coin is tossed 3 times (0 denotes tails and 1 denotes heads). Further let and . Give each of the following sets in list form, using bit-string notation:
Let . This is the set of outcomes when a coin is tossed twice (0 denotes tails and 1 denotes heads). Give in list form.
A standard card deck can be modeled by the product set
where the first coordinate encodes the denomination or kind (ace, 2-10, jack, queen, king) and where the second coordinate encodes the suit (clubs, diamonds, hearts, spades). Sometimes we represent a card as a string rather than an ordered pair (for example ). For the problems in this subsection, the card deck is the universal set.
For the problems in this subsection, the universal set is .