Show that
-
for
-
for
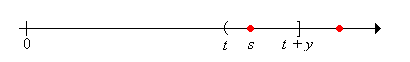
-
for
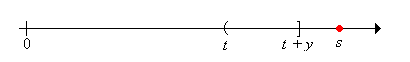
Many quantities of interest in the study of renewal processes can be described by a special type of integral equation known as a renewal equation. Renewal equations almost always arise by conditioning on the time of the first arrival and by using the defining property of a renewal process--the fact that the process restarts at each arrival time, independently of the past. However, before we can study renewal equations, we need to develop some additional concepts and tools involving measures, distribution functions, integrals, convolutions, and transforms. In many ways, these parallel our previous study of probability measures, probability distribution functions, expected value, convolution of probability density functions, and generating functions. Hopefully, these parallels will make the study easier.
Suppose that is a positive measure (or distribution) on with the property that for each and (quite possible infinite). We will also use to denote the corresponding distribution function:

Hopefully, the notation will not cause confusion and it will be clear from context whether refers to the measure (a set function) or the distribution function (a point function). The basic structure of a positive measure and its associated distribution function occurred several times in our preliminary discussion of renewal processes:
Suppose that and that .
The function satisfies many of the basic properties of a cumulative distribution function. Moreover, the proofs are essentially the same; in fact, the proofs follow from Exercise 1. As usual, we will let denote the limit of from the left at . By convention, we will let
Show that
A measure on is completely determined by its values on intervals, so it follows that the measure is completely determined by the distribution function . Equivalently, a function that satisfies properties (a), (b), (c), and (d) of Exercise 2 defines a measure through (e), (f), (g), and (h). In almost all cases, the measure will be discrete, continuous, or mixed, in analogy to the discrete, continuous, and mixed probability distributions that we have studied.
First, is discrete if there exists a countable set and a function where from into such that
Thus, the measure is concentrated at the discrete set of points and is the measure at . The function is the density function of the measure with respect to counting measure.

Next, is continuous if there exists a function from into such that
Thus,
has no points of positive measure. The function
is the density function of the measure
with respect to standard Lebesgue measure (length measure) on
.
For our purposes,
will be a nice
function that is integrable in the ordinary calculus sense.

Finally, is mixed if it is the sum of a discrete and continuous measure. That is, there exists countable set and a function from into as well as a function from into such that
Thus, part of the measure is concentrated at the discrete set of points and the rest of the measure is continuously spread out over .

Suppose now that is a function from into , and that is a (measurable) subset of . We will denote the integral of on the set with respect to the measure by
We will not go into the technical details of the general definition of this integral. However, in the discrete, continuous, and mixed cases, the integral is very similar to the definitions that we have given for expected value. First, suppose that is a discrete measure with discrete density as defined above. Then
Next, suppose that is a continuous measure with density function as defined above. Then
Finally, suppose that is a mixed measure with density functions and , as defined above. Then
This general integral satisfies the essential properties of any integral, which are given in the following exercises. Give proofs at least in the discrete and continuous cases. Assume that and are (measurable) functions on , is a constant, and is a (measurable) subset of . Assume also that the indicated integrals exist.
The integral is a linear operation:
The integral is a monotone operator:
In the remainder of this section, unless otherwise noted, we will denote the integral over the closed interval by
As above, suppose that is a positive measure on and that is a function from into . The convolution of the function with the distribution is the function defined by
This is a different use of the word than in our previous study of the convolution of probability density functions, but there is a close connection.
Suppose that is a probability distribution with density function and that is a probability density function (either both discrete or both continuous). Show that where the convolution on the right is the ordinary convolution of probability density functions. Recall that this function is the probability density function of the sum of two independent random variables, one with probability density function and one with probability density function .
Convolution is associative. Suppose that and are measures on and that is a function on . Show that
Convolution is linear. Suppose that is a measure on , that and are functions on , and that is a constant. Show that
In general, the commutative property does not make sense since the function and the measure are different types of objects. In the special case that the function is the cumulative function of a measure, the commutative property does hold.
Suppose that and are measures on . Show that
Armed with our new analytic machinery, we can return to the study of renewal processes. Thus, suppose that we have a renewal process with interarrival distribution function and renewal function . Recall that each of these functions defines a positive measure on , as discussed above. Of course, the measure associated with is actually a probability measure.
The distributions of the arrival times are the convolution powers of . Show that .
Suppose now that and are functions on , with known and unknown. An integral equation of the form
is called a renewal equation for . Usually, where is a random process of interest associated with the renewal process. The renewal equation comes from conditioning on the first arrival time , and then using the defining property of the renewal process--the fact that the process starts over, interdependently of the past, at the arrival time.
Condition on the first arrival time to show that .
Thus, the renewal function itself satisfies a renewal equation. Of course, we already have a formula
for
, namely
.
However, sometimes
can be computed more easily from the renewal equation directly.
The following exercises give the fundamental results on the solution of the renewal equation.
Show that is a solution of the renewal equation . Moreover, show that if is locally bounded, then is locally bounded and is the unique such solution. The steps are given below.
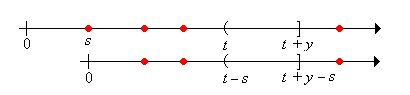
Let denote the remaining life at time and for , let
We will derive and then solve a renewal equation for by conditioning on the time of the first arrival. We can then find integral equations that describe the distribution of the current age and the joint distribution of the current and remaining ages.
Show that

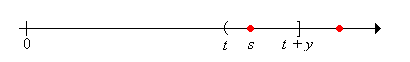
Now let for (the right-tail distribution function of an interarrival time), and for , let
Condition on the time of the first arrival and use the result of the previous exercise to show that satisfies the renewal equation
Solve the renewal equation to show that
Now let denote the current age at time and recall that for . Use this result and the Exercise 14 to show that
Next recall that for and . Use this result and Exercise 14 to show that
Consider the renewal process with interarrival times uniformly distributed on . Thus the probability distribution function of an interarrival time is for . The renewal function can be computed from the renewal equation in Exercise 10 by successively solving differential equations.
Show that for :
Show that for :
Recall that the Poisson process has interarrival times that are exponentially distributed with rate parameter . Thus, the interarrival distribution function is for .
Use the renewal equation in Exercise 10 to give another proof that the renewal function is for .
Use the result of Exercise 16 to give another derivation of the joint distribution of .
Consider the renewal process for which the interarrival times have the geometric distribution with parameter :
The arrivals are the successes in a sequence of Bernoulli trials. The number of successes in the first trials is the counting variable for .
Use the renewal equation in Exercise 10 to give another proof that the renewal function is for .
Use the result of Exercise 16 to give another derivation of the joint distribution of for