A renewal process is an idealized stochastic model for events
that occur randomly in time. These temporal events are generically referred to as renewals or arrivals. Here are some typical interpretations and applications.
customersarriving at a
service station. Again, the terms are generic. A customer might be a person and the service station a store, but also a customer might be a file request and the service station a web server.
The basic model actually gives rise to several interrelated random processes: the sequence of interarrival times, the sequence of arrival times, a counting process, and several age
processes. In this section we will define and study the basic properties of each of these processes in turn.
Let denote the interarrival time, that is, the time between the and arrivals. Our basic assumption is that is a sequence of independent, identically distributed, random variables. In statistical terms, corresponds to sampling from the distribution of a generic interarrival time . We assume that and , so that the interarrival times are nonnegative, but not identically 0. Let denote the common mean of the interarrival times. We allow that possibility that .
On the other hand, show that .
If , we will let denote the common variance of the interarrival times. Let denote the common distribution function of the interarrival times, so that
The distribution function turns out to be of fundamental importance in the study of renewal processes. We will let denote the probability density function of the interarrival times if the distribution is discrete or if the distribution is continuous and has a density function.
The renewal process is said to be periodic if there exists a positive number such that . The largest such is the period.
Let
We follow our usual convention that the sum over an empty index set is 0; thus . On the other hand, is the time of the arrival for . The sequence is called the arrival time process, although note that is not considered an arrival. A renewal process is so named because the process starts over, independently of the past, at each arrival time.
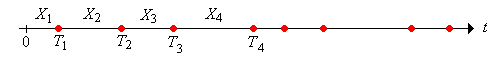
The sequence is the partial sum process associated with the independent, identically distributed sequence of interarrival times . Partial sum processes associated with independent, identically distributed sequences have been studied in several places in this project. In the remainder of this subsection, we will collect some of the more important facts about such processes.
First, we will let denote the distribution function of , so that
Recall that if has probability density function (in either the discrete or continuous case), then has probability density function , the -fold convolution power of .
Recall that the sequence of arrival times has stationary, independent increments:
Show or recall that
Recall the law of large numbers: as :
Show that as with probability 1.
For , let denote the number of arrivals in the interval :
We will refer to the random process as the counting process.
Show that for .
Show that if then is the number of arrivals in .
Note that as a function of , is a (random) step function. with jumps at the distinct values of ; the size of the jump at an arrival time is the number of arrivals at that time. In particular, is an increasing function of .
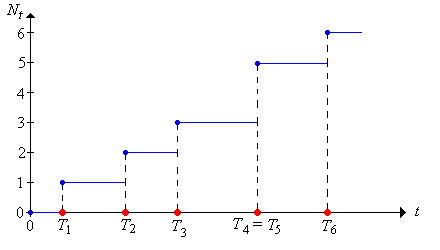
More generally, we can define the (random) counting measure corresponding to the sequence of random points in . Thus, if is a (measurable) subset of , we will let denote the number of the random points in :
In particular, note that with our new notation,
and
.
Thus, the random counting measure is completely determined by the counting process. The counting process is the cumulative measure function
for the counting measure, analogous the cumulative distribution function of a probability measure.
Show that for and ,
Prove the following results:
All of the exercises so far in this subsection show that the arrival time process and the counting process are inverses of one another in a sense. The important equivalences in Exercise 8 can be used to obtain the probability distribution of the counting variables in terms of the interarrival distribution function .
Show that for and ,
The expected number of arrivals up to time is known as the renewal function:
The renewal function turns out to be of fundamental importance in the study of renewal processes. Indeed, the renewal function essentially characterizes the renewal process. It will take awhile to fully understand this, but as a first step, the expansion in terms of indicator variables leads to a nice connection between the renewal function and the interarrival distribution function.
Show that
Note that we have not yet shown that , and note also that this does not follow from the previous exercise. However, we will establish this finiteness condition in the subsection on Moment Generating Functions below.
More generally, if is a (measurable) subset of , let , the expected number of arrivals in .
Show that is a positive measure on the measurable subsets of ; this measure is known as the renewal measure.
Show that
Show that if then , the expected number of arrivals in
The last exercise implies that the renewal function actually determines the entire renewal measure. The renewal function is the cumulative measure function
, analogous to the cumulative distribution function of a probability measure. Thus, every renewal process naturally leads to two measures on
,
the random counting measure corresponding to the arrival times, and the measure associated with the expected number of arrivals.
For , show that . That is, is in the random renewal interval .
In the language of reliability, the random variable
is called the current life at time . This variable takes values in the interval and is the age of the device that is in service at time . The random process is the current life process.
The random variable
is called the remaining life at time . This variable takes values in the interval and is the time remaining until the device that is in service at time fails. The random process is the remaining life process.
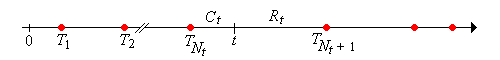
Finally, the random variable
is called the total life at time ; this variable gives the total life of the device that is in service at time . The random process is the total life process.
Tail events of the current and remaining life can be written in terms of each other and in terms of the counting variables. Suppose that , , and . Show that
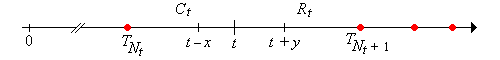
Of course, the various equivalent events in the last exercise must have the same probability. In particular, it follows that if we know the distribution of for all then we also know the distribution of for all , and in fact we know the joint distribution of and for all and hence also the distribution of for all .
The basic comparison in the following exercise is often useful, particularly for obtaining various bounds. The idea is very simple: if the interarrival times are shortened, the arrivals occur more frequently.
Suppose now that we have two interarrival sequences, and defined on the same probability space, with (with probability 1) for each . Show that
Suppose that is a sequence of Bernoulli trials with success parameter . Recall that is a sequence of independent, identically distributed indicator variables with . We have studied a number of random processes derived from :
It is natural to view the successes as arrivals in a discrete-time renewal process.
Consider the renewal process with interarrival sequence .
It follows that the renewal measure is proportional to counting measure on .
Run the binomial timeline experiment 1000 times with an update frequency of 10 for various values of the parameters and . Note the apparent convergence of the empirical distribution of the counting variable to the true distribution.
Run the negative binomial experiment 1000 times with an update frequency of 10 for various values of the parameters and . Note the apparent convergence of the empirical distribution of the arrival time to the true distribution.
Consider again the renewal process with interarrival sequence . For , show that
This renewal process starts over, independently of the past, not only at the arrival times, but at fixed times as well. The Bernoulli trials process (with the successes as arrivals) is the only discrete-time renewal process with this property, which is a consequence of the memoryless property of the geometric interarrival distribution.
We can also use the indicator variables as the interarrival times. This may seem strange at first, but actually turns out to be useful.
Consider the renewal process with interarrival sequence .
The age processes are not very interesting for this renewal process. Show that with probability 1,
As an application of the last renewal process, we can show that the moment generating function of the counting variable in an arbitrary renewal process is finite in an interval about 0 for any . This implies that has finite moments of all orders and in particular that for any .
Suppose that is the interarrival sequence for a renewal process. By the basic assumptions, there exists such that
We now consider the renewal process with interarrival sequence , where
The renewal process with interarrival sequence is just like the renewal process in Exercise 22, except that the arrival times occur at the points in the sequence .
For each , has finite moment generating function in an interval about 0.
The Poisson process, named after Simeon Poisson, is the most important of all renewal processes. The Poisson process is so important that it is treated in a separate chapter in this project. Please review the essential properties of this process:
Consider again the Poisson process with rate parameter . For , show that
The Poisson process starts over, independently of the past, not only at the arrival times, but at fixed times as well. The Poisson process is the only renewal process with this property, which is a consequence of the memoryless property of the exponential interarrival distribution.
Run the Poisson experiment 1000 times with an update frequency of 10 for various values of the parameters and . Note the apparent convergence of the empirical distribution of the counting variable to the true distribution.
Run the gamma experiment 1000 times with an update frequency of 10 for various values of the parameters and . Note the apparent convergence of the empirical distribution of the arrival time to the true distribution.