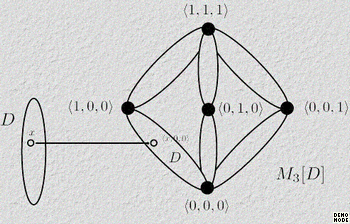
The M3[D] construction
Let D be a bounded
distributive lattice, and let M3 = {0, a, b, c, 1}
be the five-element nondistributive modular lattice.
Let M3[D] denote
the
subposet of D3 consisting of all <x, y, z>
satisfying x
y
= y z
= z x.
We call such
a triple balanced. Then the following statements hold:
1. M3[D] is a modular lattice.
2.
The subset M3
= {<0, 0, 0>, <1, 0, 0>, <0, 1, 0>, <0, 0, 1>,
<1, 1,1>} of M3[D]
is a sublattice of M3[D]
and it is isomorphic to M3.
3.
The subposet D
= {<x, 0, 0>}{x in D} of
M3[D] is isomorphic
to
D; we identify D with D.
4.
M3
and D generate M3[D].
5.
Let θ be
a congruence relation of D = D; then there is a unique
congruence θ
of M3[D] θ
restricted to ol D is θ ; therefore, Con
M3[D]
Con D.
This was introduced in E. T. Schmidt, Zur Characterisierung der Kongruenzverbande der Verbande, Math. Csasopis 18 (1968), 3-20.
