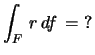
1. Vizsgazárthelyi megoldásokkal
1999/2000 tél II. évf. 13.-18.tk.
1. Legyen F a z-tengelyu R sugarú
m magasságú egyenes körhengerpalást.
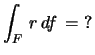
MO.
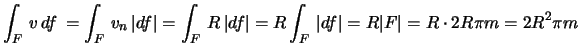
2.
Számítsuk ki a div
![]() értékét
minden
értékét
minden
![]() esetén!
esetén!
MO.
div
![]() ,
mert
,
mert
![]() (pl. azért mert
(pl. azért mert
![]() antiszimmetrikus) és
antiszimmetrikus) és
![]() ,
így skalárszorzatuk 0.
,
így skalárszorzatuk 0.
3.
Legyen H az a háromszögvonal, melynek csúcsai a
![]() pontok. Legyen
pontok. Legyen
v(x,y)=(x2-2y,2x+y2) minden
![]() -re.
-re.
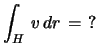
MO.
rot
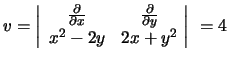 így Stokes tétellel (F a H által bezárt
háromszöglap):
így Stokes tétellel (F a H által bezárt
háromszöglap):
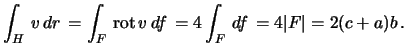
4. A derivált definíciója alapján
állapítsa meg, hogy hol deriválható az
![]() függvény!
függvény!
MO.
Csak az origóban, mert
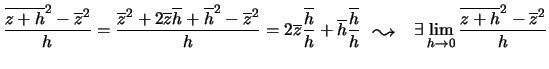
IFF z=0
hiszen
![${\displaystyle \vert\frac{\overline{h}}{h}\vert=1\mbox{\,\,\,\,\raisebox{-0.5mm...
...}
\overline{h}\frac{\overline{h}}{h}
\xrightarrow[h \longrightarrow 0]{} 0\,,}$](img17.gif) továbbá
továbbá
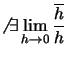 és
két olyan függvény összegének nincs határértéke,
melyek közül pontosan egynek van.
és
két olyan függvény összegének nincs határértéke,
melyek közül pontosan egynek van.
5. Adja meg az
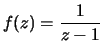 függvény
z = 1 és z = 0 körüli összes
Laurent sorát!
MO.
függvény
z = 1 és z = 0 körüli összes
Laurent sorát!
MO.
a) z = 1:
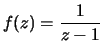
b) z = 0:
1)
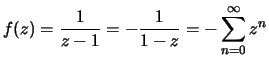 2)
2)
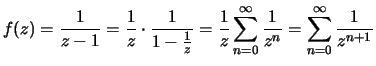
6.
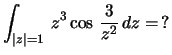
MO.
Az
![]() függvény origó körüli Laurent-sora:
függvény origó körüli Laurent-sora:
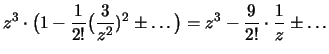 ,
így Res
z=0f(z)= -4,5 tehát
residuum tétellel:
,
így Res
z=0f(z)= -4,5 tehát
residuum tétellel: