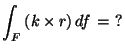
4. Vizsgazárthelyi megoldásokkal
1999/2000 tél II. évf. 13.-18.tk.
1. Legyen F a z-tengelyu R sugarú
m magasságú egyenes körhengerpalást.
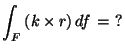
MO.
 .
Ugyanis F normálisa
.
Ugyanis F normálisa
![]() ,
azaz n benne van a k és r által
kifeszített síkban, míg persze
,
azaz n benne van a k és r által
kifeszített síkban, míg persze
![]() .
Következésképp az integrandus minden pontban
meroleges a felületi normálisra, azaz az integrál 0.
.
Következésképp az integrandus minden pontban
meroleges a felületi normálisra, azaz az integrál 0.
VAGY:
![]()
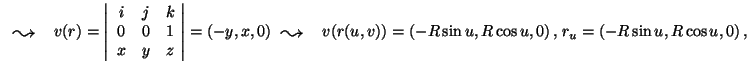
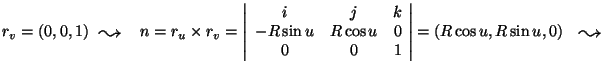
![]()
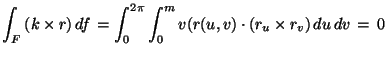
2. Számítsuk ki a
rot
![]() értékét
minden
értékét
minden
![]() esetén!
esetén!
MO.
rot
![]() , mert
, mert
![]() , mert
, mert
![]() antiszimmetrikus lin. op., vagy mert ahogy a fenti
pl.-ban láttuk
antiszimmetrikus lin. op., vagy mert ahogy a fenti
pl.-ban láttuk
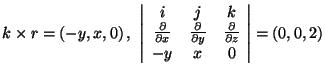 .
.
3.
Legyen K az [xy] síkbeli origóközéppontú
körvonal, mint kifele irányított kétdimenzióbeli
felület és
![]() minden
minden
![]() -re.
-re.
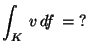
MO. div
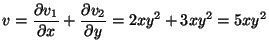 így
Gauss-Osztrogradszkij tétellel (F a K által bezárt
körlap):
így
Gauss-Osztrogradszkij tétellel (F a K által bezárt
körlap):
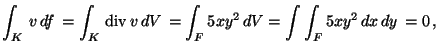 mert F az y tengelyre szimmetrikus és az integrandus
x-ben páratlan.
mert F az y tengelyre szimmetrikus és az integrandus
x-ben páratlan.
4. Legyen
![]() az
origón kívül és
g(0,0) = 0, továbbá
f(z)=f(x+jy)=g(x,y)+jg(x,y). Állapitsa meg, hogy
az origóban:
az
origón kívül és
g(0,0) = 0, továbbá
f(z)=f(x+jy)=g(x,y)+jg(x,y). Állapitsa meg, hogy
az origóban:
a) fennállnak-e a Cauchy-Riemann differenciáegyenletek b) deriválható-e az f függvény!
MO. a) Igen:
![]() .
b) Nem:
u(x,y)=v(x,y)=g(x,y) nem deriválható az
origóban, hiszen nem is folytonos itt:
.
b) Nem:
u(x,y)=v(x,y)=g(x,y) nem deriválható az
origóban, hiszen nem is folytonos itt:
![]() .
.
5. Adja meg az
![]() függvény
origó körüli azon Laurent sorait, melyek a
a
függvény
origó körüli azon Laurent sorait, melyek a
a
![]() ill. a z=3 pontokban
eloállítják a fúggvényt és mutassa is
meg, hogy a megfelelo sor ott valóban
eloállítja a függvényt!
MO.
a) |z| < 1:
ill. a z=3 pontokban
eloállítják a fúggvényt és mutassa is
meg, hogy a megfelelo sor ott valóban
eloállítja a függvényt!
MO.
a) |z| < 1:
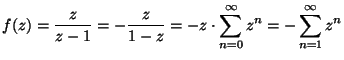
b) |z| > 1:
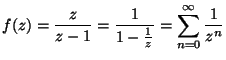
c)
![]()
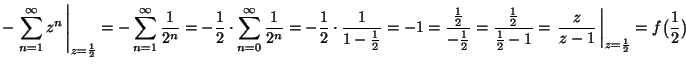
![]()
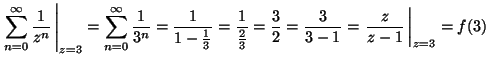
6.
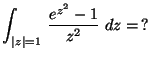
MO. Az integrál 0, mert
![${\displaystyle
f(z)= \frac{e^{z^2}-1}{z^2}
\xrightarrow[z \rightarrow \,0]{} 1 \mbox{\,\,\,\,\raisebox{-0.5mm}{\Large$\leadsto$ }\,\,\,\,}f(z)}$](img34.gif) -nek az egyetlen a
körlapon levo
szingularitásában, az origóban megszüntetheto
szakadása van.
-nek az egyetlen a
körlapon levo
szingularitásában, az origóban megszüntetheto
szakadása van.