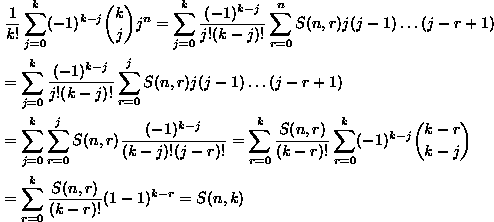
KOMBINATORIKA
3.2.4. Tétel
Bizonyítás:
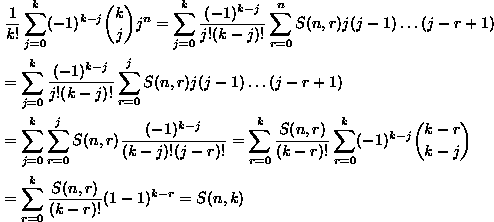
ANALÍZIS
Gyakorló feladat
21. 
? Az integrandust helyettesí
téssel alakítjuk át.
Legyen 
, ebbol 
és 
.
Az új határok: ha x=3, akkor u=2, és ha 
,
akkor 
.
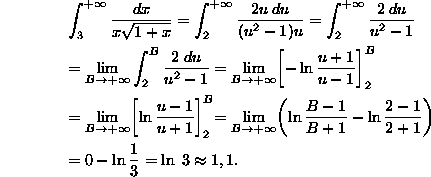
SZÁMELMÉLET
Az Euler-féle 
függvény
A modulo m redukált maradékosztályok számát 
-mel
szoktuk jelölni, és 
értéke legyen definició szerint
1. Az így definiált számelméleti függvényt Euler-féle
függvénynek nevezzük. Könnyen látható, hogy a 
függvénynek a definiciója ekvivalens az alábbival:
Legyen n tetszoleges természetes szám. Az n-hez relatív
prím n-nél nem nagyobb pozitív egész számok
számát -nel jelöljük.
Igazolható, hogy a számelméleti függvény
multiplikatív,
azaz ha m,n egymáshoz relatív prím természetes számok,
akkor
Ezt az összefüggést felhasználva, a függvény
explicit
alakja könnyen meghatározható: ha az n>1 természetes szám
kanonikus alakja
LINEÁRIS ALGEBRA
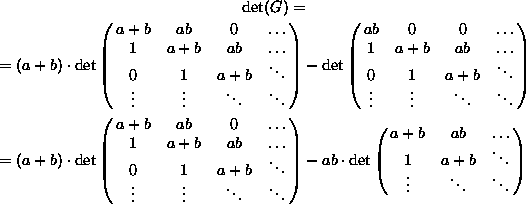
203 Számítsa ki az alábbi mátrix determinánsát!
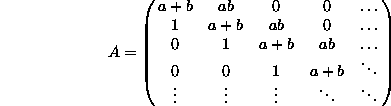
Útmutatás: az elso sor szerinti kifejtéssel:
