Elsőnek vizsgáljuk meg, hogy az egyszerű kockarács D-szimbólumát hogyan
készítjük el. Először is vegyünk egy kockát, és állítsuk elő az optimális
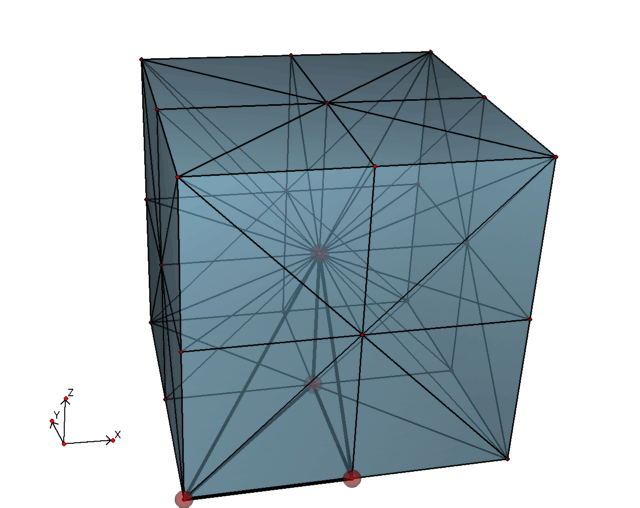
baricentrikus felbontását (1. ábra). Az optimális baricentrikus
felbontás megőrzi az eredeti alakzat minden szimmetriáját, ezért a
testközéppontot, majd egy lapközéppontot, egy élközéppontot végül egy csúcsot
kell vennünk.
Figure:
A kocka teljes baricentrikus felbontása, illetve
egyetlen szimplex a felbontásból
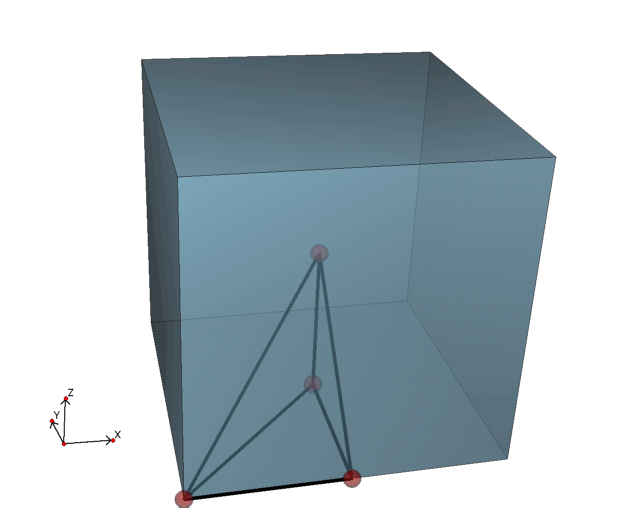 |
Látható, hogy az összes előálló szimplex egybevágó, és így síkra tükrözésekkel
egymásba vihetők,2így egyetlen egy
szimplex-pályát kell csak vizsgálni. Tehát a D-diagram 1 elemű (lásd
fig:kocka1d. ábrát). Az 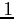 -elemű D-diagramon jelöltük a hurok-éleket is,
de a továbbiakban az átláthatóság könnyítése érdekében elhagyjuk. (A D-diagram
minden csúcsából kiindul mindegyik színű él, így most
-elemű D-diagramon jelöltük a hurok-éleket is,
de a továbbiakban az átláthatóság könnyítése érdekében elhagyjuk. (A D-diagram
minden csúcsából kiindul mindegyik színű él, így most 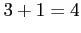 ``szín'' azaz
``jel'' lép fel.)
``szín'' azaz
``jel'' lép fel.)
Figure:
A kockarács leggazdagabb szimmetriájú
(automorfizmus) egybevágóság csoportjához tartozó D-diagram
|
Most állítsuk elő a kockakövezés
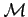 mátrix-függvényét. Mivel
egy szimplex-pályáról beszélünk, ez csak egy mátrix. Konkrétan a következő:
mátrix-függvényét. Mivel
egy szimplex-pályáról beszélünk, ez csak egy mátrix. Konkrétan a következő:
3 dimenziós Euklideszi poliéderrács esetén (de más terek egyféle poliéderrel történő kövezésénél is) a következőt jelentik a szabad paraméterek értékei:
-
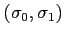 : az
: az  mátrixelem azt mutatja, hogy a
poliéder megfelelő lapja hány oldalú
mátrixelem azt mutatja, hogy a
poliéder megfelelő lapja hány oldalú
-
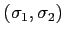 : a megfelelő csúcsban hány él találkozik csak a
tekintett baricentrikus szimplexhez tartozó poliéderen
: a megfelelő csúcsban hány él találkozik csak a
tekintett baricentrikus szimplexhez tartozó poliéderen
-
 : a megfelelő él hány rács poliéder közös éle.
: a megfelelő él hány rács poliéder közös éle.
Ezzel egybevág a fenti mátrix: 4 oldalú a kocka egy lapja, 3 él indul ki egy
csúcsból és 4 kocka találkozik egy élben.
Boroczki Lajos
2007-05-29
![]() -elemű D-diagramon jelöltük a hurok-éleket is,
de a továbbiakban az átláthatóság könnyítése érdekében elhagyjuk. (A D-diagram
minden csúcsából kiindul mindegyik színű él, így most
-elemű D-diagramon jelöltük a hurok-éleket is,
de a továbbiakban az átláthatóság könnyítése érdekében elhagyjuk. (A D-diagram
minden csúcsából kiindul mindegyik színű él, így most ![]() ``szín'' azaz
``jel'' lép fel.)
``szín'' azaz
``jel'' lép fel.)
![]() mátrix-függvényét. Mivel
egy szimplex-pályáról beszélünk, ez csak egy mátrix. Konkrétan a következő:
mátrix-függvényét. Mivel
egy szimplex-pályáról beszélünk, ez csak egy mátrix. Konkrétan a következő:
