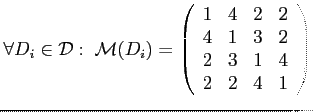Kockarács szimmetria töréssel

Most vegyük a kockarácsot úgy, hogy a baricentrikus felbontás nem őrzi meg a kockarács leggazdagabb (teljes) szimmetriacsoportját, azaz szegényebb szimmetriacsoporthoz több baricentrikus szimplexből ragasztjuk össze a megfelelő (éppen ez által értelmezett) szimmetriacsoportnak egy alaptartományát. (Így tudunk a legegyszerűbben nagyobb elemszámú D-szimbólumokat előállítani, továbbá a kockarács lapjainak, éleinek deformálásával.) A következő példában hat különböző szimplex-pályára bontjuk a kockarácsot. A testközéppontot megtartjuk a kocka belső pontjának, és a kocka csúcsait pedig a baricentrikus felbontás csúcsainak. Az egyik lapon megtartjuk a lapközéppontot is, csak az élközéppontot változtatjuk meg. 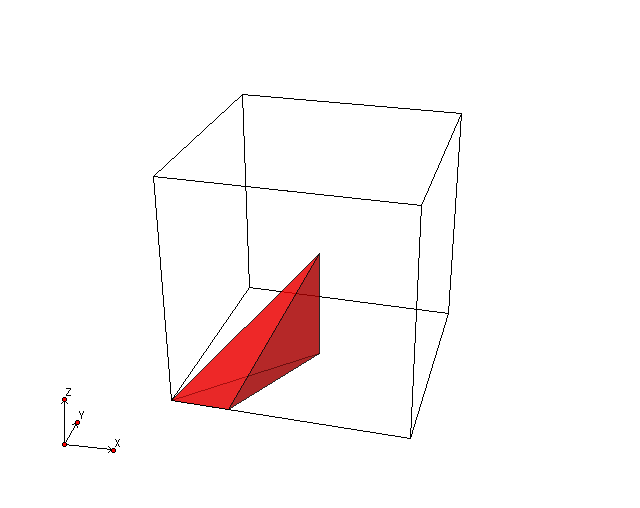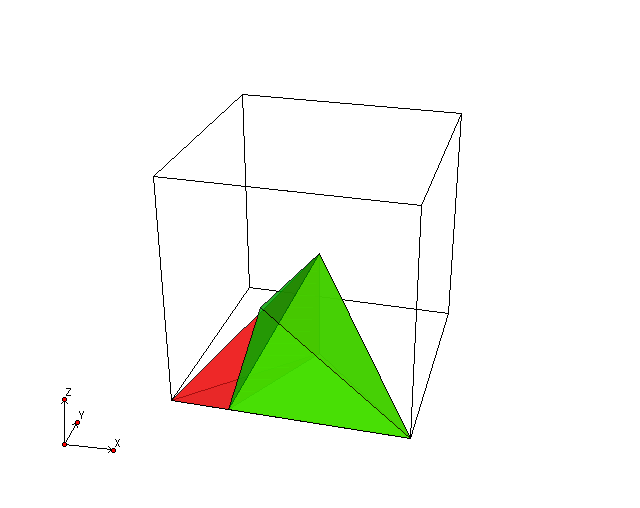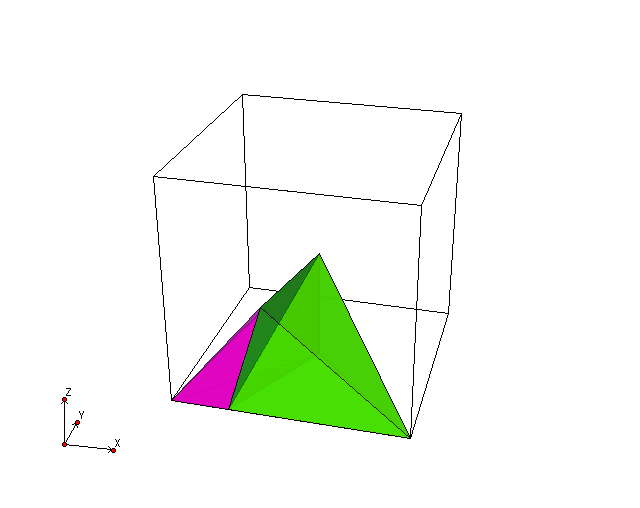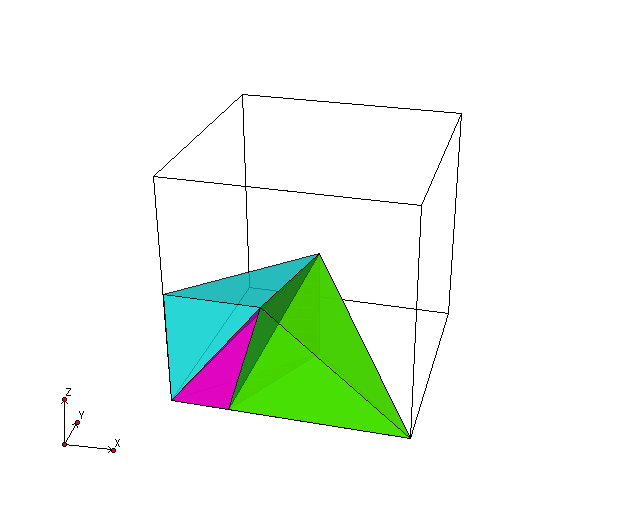A szomszédos lapokon pedig az előző éllel párhuzamosan toljuk el a lapközéppontot, de az eddig nem rögzített élközéppontot megtartjuk az él közepén. 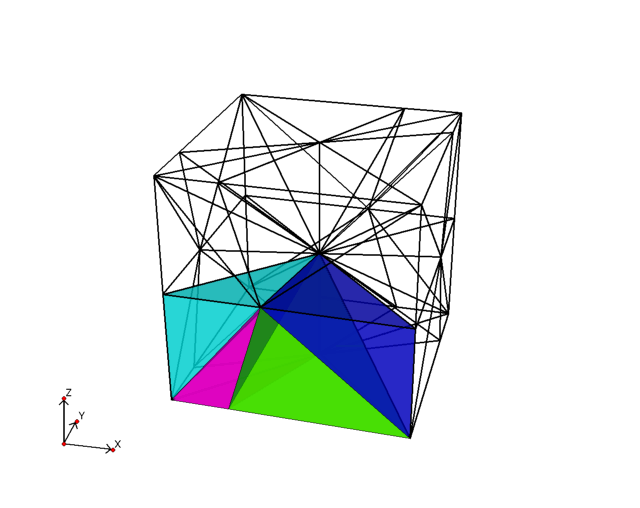A fundamentális tartomány felépülése fig:kocka2f. ábrán látható, míg a kocka teljes baricentrikus felbontása fig:kocka2b. ábrán.

Figure: A fundamentális tartomány felépülése

Figure: A teljes baricentrikus felbontás

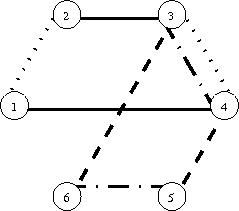
Láthatjuk, hogy hatféle szimplexből raktuk össze a kockát, azaz hat szimplex-pálya van, így hatelemű a D-szimbólum, a diagramja a 109-es sorszámú a felsorolásunk szerint (fig:kocka2d. ábrán látható a hurokélek törlésével). Az 1-es pontja a piros szimplex, a 2-es a sárga, a 3-as a zöld, a 4-es a lila, az 5-ös a türkiz és a 6-os a sötétkék.

Figure: Az elrontott kockakövezés diagramja

Mivel az előző kockarácsot ``rontottuk el,'' ezért a mátrix-függvény ugyanaz:

$$\forall D_i\in\mathcal{D}:\; \mathcal{M}(D_i)= \left( \begin{arra... ...& 4 & 2 & 2\ 4 & 1 & 3 & 2\ 2 & 3 & 1 & 4\ 2 & 2 & 4 & 1 \end{array} \right)$$