Most vegyünk egy másik fajta, szintén lexikografikus jellegű rendezést
M96 cikk alapján. A következő lépésekre van szükségünk:
- Bevezetünk egy sorszámozást, ami minden adott kezdőpontú, összefüggő
D-szimbólum csúcsainak sorszámát megadja.
- Az előbbi sorszámozás alapján veszünk egy távolságot.
- A csúcsok távolsága alapján veszünk egy rendezést adott kezdőpontú
diagramok között.
- Felsoroljuk az összes lehetséges diagramot növekvő sorrendben.
- Eközben eldobáljuk a rosszakat.
Bármely két elem távolságát meghatározhatjuk úgy, hogy az egyik elemmel indított
sorszámozás szerint a második elemnek a sorszámát vesszük. 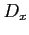 és
és 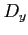 távolságának jelölése:
távolságának jelölése: 
Ez a távolság a következő rendezési algoritmushoz vezet:
Algoritmus 3.2
Legyenek
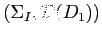 és
és
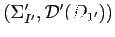 két D-szimbólum diagramjai,
kitüntetett kezdőponttal. Azt mondjuk, hogy
két D-szimbólum diagramjai,
kitüntetett kezdőponttal. Azt mondjuk, hogy
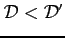 a
következő tulajdonságok alapján:
a
következő tulajdonságok alapján:
 (dimenzió)
(dimenzió)
- Ha megegyeznek:
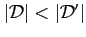 (D-szimbólum elemszáma)
(D-szimbólum elemszáma)
- Ha egyenlőség áll:
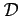 és
és
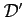 elemeinek
távolságait hasonlítjuk össze:
elemeinek
távolságait hasonlítjuk össze:
Ha végig egyenlőség állt, a két diagram izomorf.
Most már meg tudjuk különböztetni a diagramokat, így fel is tudjuk sorolni a
különbözőeket:
Algoritmus 3.3
Egy backtrack3 algoritmust használunk a felsorolásra. Minden lépésben
megpróbáljuk a soron következő élt kihagyni, majd hozzáadni; és az élek
sorának végére érve ellenőrizzük, hogy jó diagramot kaptunk-e. Ha igen,
eltároljuk későbbi elemzésre, különben eldobjuk. Az éleket a forrás, a cél és
az operáció sorszámával azonosítjuk, ahol a forrás mindig határozottan kisebb,
mint a cél, ezzel tudjuk biztosítani az él és az azonosítás közötti egy-egy
értelmű hozzárendelést.
Az algoritmus bemenete a 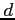 dimenzió és a diagram csúcsainak
dimenzió és a diagram csúcsainak  száma.
Minden állapotban a következő lépéseket tesszük meg:
száma.
Minden állapotban a következő lépéseket tesszük meg:
- Ha a forrás sorszáma egyenlő a csúcsok számával, akkor megnézzük, hogy
összefüggő-e a gráf (egyszerű szélességi bejárással, sec:kdim
részben kicsit bővebben kifejtve), majd előállítjuk
alg:sorsz algoritmus alapján az első csúcsot kezdőpontnak vett
sorszámozást. Ha ez nem ugyanaz, mint a backtrack algoritmus által
előállított sorszámozás, akkor eldobjuk, mert előállítja a
backtrack algoritmus a jó sorszámozást is. Sorban előállítjuk a többi
csúcs által generált sorszámozást is, és ha ezek közül bármelyik kisebb
diagramot ad, akkor eldobjuk, mert a backtrack algoritmus a kisebbet is
előállítja. Végül elkészítjük a diagram alapján az
 mátrix-függvényt, és megvizsgáljuk, hogy a főátlótól legalább
mátrix-függvényt, és megvizsgáljuk, hogy a főátlótól legalább  távolságra levő mezőkben 1-es vagy 2-es szerepel-e (csak így lehet az
távolságra levő mezőkben 1-es vagy 2-es szerepel-e (csak így lehet az
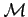 mátrix-függvény megfelelő helyein 2-es), ha valamelyikben
nem az szerepelne, akkor szintén eldobjuk. Ha idáig eljutottunk, beszúrjuk
egy rendezett adatrendszerbe (az előbb definiált rendezés szerint.) Ha már
szerepelne a rendszerben, akkor eldobjuk, mert ez azt jelenti, hogy
szimmetrikus a diagram, és egyszer már szerepelt.
mátrix-függvény megfelelő helyein 2-es), ha valamelyikben
nem az szerepelne, akkor szintén eldobjuk. Ha idáig eljutottunk, beszúrjuk
egy rendezett adatrendszerbe (az előbb definiált rendezés szerint.) Ha már
szerepelne a rendszerben, akkor eldobjuk, mert ez azt jelenti, hogy
szimmetrikus a diagram, és egyszer már szerepelt.
- Ha a forrás sorszáma kisebb, mint a csúcsok száma, akkor először
meghívjuk rekurzívan az eljárást a következő élre. Végül, ha hozzá tudjuk
adni a vizsgált élt a rendszerhez, akkor hozzáadjuk, meghívjuk rekurzívan
az eljárást ugyanarra az élre, amit vizsgáltunk, majd töröljük a
hozzáadott élt.
- Az éleket lexikografikus sorrendben vesszük: első a forrás sorszáma,
második az operáció sorszáma és utolsó a cél sorszáma. A forrás és a cél
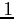 és
és
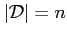 között változik (figyelve, hogy a cél szigorúan
nagyobb a forrásnál) és az operáció
között változik (figyelve, hogy a cél szigorúan
nagyobb a forrásnál) és az operáció 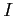 -beli.
-beli.
- Egy apró heurisztikát használunk: ha a forrás csúcsnak nincs éle,
akkor nem hívjuk meg a következő forrásra az eljárást él hozzáadás nélkül,
mivel így nem lehet összefüggő a diagram.4
Lemma 3.4
Az  dimenziós
dimenziós
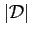 elemű D-szimbólumok lehetséges diagramjai
rendezetten szerepelnek alg:backtrack algoritmusbeli rendezett
adatrendszerben. (De nem tartozik minden diagramhoz D-szimbólum, mert még
nem vizsgáltuk meg az
elemű D-szimbólumok lehetséges diagramjai
rendezetten szerepelnek alg:backtrack algoritmusbeli rendezett
adatrendszerben. (De nem tartozik minden diagramhoz D-szimbólum, mert még
nem vizsgáltuk meg az
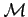 mátrix-függvényeket.)
mátrix-függvényeket.)
Mivel felsoroltuk az összes lehetséges diagramot, és csak az azonosakat,
illetve az
 mátrix-függvény alapján rosszakat hagytuk el, ezért az
állítás triviális. Az adatrendszert nem részletezzük, mivel egy egyszerű láncolt
lista is megteszi egyelőre, amíg nem túl nagy a jó diagramok száma. Legalább
9-10 elemű D-szimbólumok felsorolása esetén viszont már érdemes lenne AVL vagy
piros-fekete fában tárolni a lehetséges diagramokat. (Magasabb szintű
programozási nyelvekben halmazként.)
mátrix-függvény alapján rosszakat hagytuk el, ezért az
állítás triviális. Az adatrendszert nem részletezzük, mivel egy egyszerű láncolt
lista is megteszi egyelőre, amíg nem túl nagy a jó diagramok száma. Legalább
9-10 elemű D-szimbólumok felsorolása esetén viszont már érdemes lenne AVL vagy
piros-fekete fában tárolni a lehetséges diagramokat. (Magasabb szintű
programozási nyelvekben halmazként.)
Boroczki Lajos
2007-05-29
![]() és
és ![]() távolságának jelölése:
távolságának jelölése: ![]()
![]() dimenzió és a diagram csúcsainak
dimenzió és a diagram csúcsainak ![]() száma.
Minden állapotban a következő lépéseket tesszük meg:
száma.
Minden állapotban a következő lépéseket tesszük meg: