Bibliography

urlstyle

1

L. Boróczki.
http://www.math.bme.hu/~boroczki/D-symbol.

2

A. Bölcskei and M. Szél-Koponyás.
Construction of D-graphs related to periodic tilings.
KoG, 6: 21-27, 2002.

3

O. Delgado-Friedrichs.
Euclidicity Criteria for Three-Dimensional Branched Triangulations.
Ph.D. thesis, University of Bielefeld, 1994.

4

O. Delgado-Friedrichs.
Data structures and algorithms for tilings i.
Theor. Comput. Sci., 303(2-3): 431-445, 2003.

5

A. W. M. Dress.
Presentation of discrete groups acting on simply connected manifolds in terms of parametrized systems of Coxeter matrices.
Advances in Math, 63: 196-212, 1987.

6

A. W. M. Dress, D. H. Huson and E. Molnár.
The classifications of face-transitive periodic three-dimensional tilings.
Acta Crystallographica, A(49): 806-817, 1993.

7

W. D. Dunbar.
Geometric orbifolds.
Revista Mat. Univ. Complutense de Madrid, 1(1,2,3): 67-99, 1988.

8

D. H. Huson.
The generation and classification of tile-k-transitive tilings of the Euclidean plane, the sphere and the hyperbolic plane.
Geometriae Dedicata, 47: 269-296, 1993.

9

Z. Lucic and E. Molnár.
Combinatorial classification of fundamental domains of finite area for planar discontinous isometry groups.
Arch. Math., 54: 511-520, 1990.

10

A. M. Macbeath.
The classification of non-Euclidean plane crystallographic groups.
Canadian J. Math., 19: 1192-1205, 1967.

11

E. Molnár.
List of D-diagrams.
Kézirat.

12

E. Molnár.
Sketch of an algorithm (of linear comlexity) for determining signature of the group 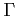$\Gamma$ of a two-dimensional Delaney-Dress-symbol.
Kézirat.

13

E. Molnár.
Symmetry breaking of the cube tiling and the spatials chess board by D-symbols.
Beitr. Alg. Geom (Contributions to Algebra and Geometry), 35(2): 205-238, 1994.

14

E. Molnár.
Discontinous groups in homogeneous Riemannian spaces by classification of D-symbols.
Publications Mathematicae, 49(3-4): 265-294, 1996.

15

E. Molnár, I. Prok and J. Szirmai.
Classification of tile-transitive 3-simplex tilings and their realizations in homogeneous spaces.
Non-Euclidean Geometries, János Bolyai memorial volume, Editors: A. Prékopa and E. Molnár, Springer.
Mathematics and its applications, 581: pp. 321-363, 2006.

16

W. P. Thurston.
Three-dimensional manifolds, Kleinian groups and hyperbolic geometry.
Bull. Amer. Math. Soc., 6: 367-382, 1992.

17

E. B. Vinberg and O. V. Shvartsman.
Discrete transformation groups of spaces of constant curvature.
Encyclopedia of Math, 29, 1993.
Geometry II.