Next: Statisztikai gépi fordítás Up: Az EM algoritmus Previous: A klasszikus példa EM Tartalomjegyzék
Az EM algoritmus különösen jól használható keverék eloszlások paramétereinek maximum likelihood becslésére, ezt a [5] cikk is elsők között említi. Ilyen esetben a számolások jelentősen leegyszrűsödnek, mivel a feladat kezelhető hiányos adat problémának. Most a kevert komponensek keverési aránya becslésének azt az esetét vizsgáljuk, amikor a komponensek sűrűsége ismert. Általánosabb, és nehezebb eset, amikor a komponensek sűrűségében is szerepelnek paraméterek, és ezeket együtt kell becsülni a keverési arányokkal. Ez az egyszerűbb eset sem valószerűtlen, mert gyakorlati példákban előfordul, hogy rendelkezésre állnak a komponensekből külön-külön vett minták is, ami által még a kevert eloszlás paramétereinek becslése előtt lehetőség nyílik a komponensek paramétereinek tetszőlegesen pontos becslésére.
Tehát tételezzük fel, hogy egy
![]() valószínűségi változó sűrűség függvényének
valószínűségi változó sűrűség függvényének ![]() komponensű kevert
alakja van:
komponensű kevert
alakja van:
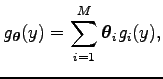
ahol
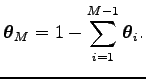
A
Ez a modell például olyan gyakorlati eseteket foglal magába, ahol például egy populáció
![]()
![]() különböző csoportra osztható bizonyos ismeretlen
különböző csoportra osztható bizonyos ismeretlen
![]() arányban. és ahol az
arányban. és ahol az ![]() -edik csoportba való tartozás feltétele mellett az
-edik csoportba való tartozás feltétele mellett az
![]() feltételes eloszlása
feltételes eloszlása
![]() Például egy Do és McLachlan által 1984-ben tekintett gyakorlati problémában, a tekintett populáció
Például egy Do és McLachlan által 1984-ben tekintett gyakorlati problémában, a tekintett populáció
![]() különböző faj
különböző faj
![]() csoportjába, részpopulációjába tartozó patkányok, melyek közül
a baglyok minden csoportból valamilyen ismeretlen
csoportjába, részpopulációjába tartozó patkányok, melyek közül
a baglyok minden csoportból valamilyen ismeretlen
![]() valószínűséggel fogyasztanak
el egy egyedet. Ez teljesülhet például, ha a
valószínűséggel fogyasztanak
el egy egyedet. Ez teljesülhet például, ha a ![]() csoport részaránya a teljes populációban
csoport részaránya a teljes populációban
![]() ,
és a baglyok minden egyedet egyforma valószínűséggel találnak meg, és fogyasztanak el, vagy lehet a
,
és a baglyok minden egyedet egyforma valószínűséggel találnak meg, és fogyasztanak el, vagy lehet a
![]() részaránya tetszőleges, de a baglyok egy ide eső egyedet olyan valószínűséggel lelnek fel, hogy
összességében
részaránya tetszőleges, de a baglyok egy ide eső egyedet olyan valószínűséggel lelnek fel, hogy
összességében
![]() valószínűséggel jussanak hozzá egy egyedhez ebből a csoportból.
A feladat a
valószínűséggel jussanak hozzá egy egyedhez ebből a csoportból.
A feladat a
![]() paraméterek becslése bagolyköpetekből vett
paraméterek becslése bagolyköpetekből vett ![]() patkánykoponyán
végzett mérések alapján, ahol egy ilyen koponyán mért adatokat tartalmazza az
patkánykoponyán
végzett mérések alapján, ahol egy ilyen koponyán mért adatokat tartalmazza az
![]() valószínűségi
változó. A patkány hozzátartozik a baglyok étrendjéhez, és az emészthetetlen részeket bagolyköpet
formájában öklendezik vissza.
valószínűségi
változó. A patkány hozzátartozik a baglyok étrendjéhez, és az emészthetetlen részeket bagolyköpet
formájában öklendezik vissza.
Tehát csupán a koponyákon végzett mérések alapján nem tudjuk meghatározni a patkányok faját, viszont tudjuk, hogy az egyes fajokon belül a mért értékek milyen eloszlást követnek. Az eloszlások ismeretében csak annak feltételes valószínűségét tudjuk meghatározni, hogy a mért értékeket feltéve mennyi a valószínűsége annak, hogy a patkány egy adott fajba tartozott, ami a csoportba tartozás indikátor változójának a várható értéke. Ha tudnánk, hogy melyik patkány milyen fajba tartozik, egyszerűen vennénk a relatív gyakoriságokat, és ezek adnák a paraméterek maximum likelihood becslését. Most azonban csak a csoportba tartozás feltételes várható értékét tudjuk, ezért a gyakoriságok számolásánál ezzel a valószínűséggel súlyozzuk az adott csoportba tartozások számát. Egy egyed esetében tehát nem vagyunk biztosak benne, hogy hová tartozik és ezért nem egy egyest adunk ahhoz a csoporthoz tartozó mintából vett gyakorisághoz, amelyik csoporthoz tartozik, hanem ezt az egyest szétosztjuk az összes csoport között annak arányában, hogy mennyi az egyed odatartozásának valószínűsége feltéve a méréseink eredményét. Így a gyakoriság már nem egész lesz, hanem tetszőleges valós szám. Persze a feltételes valószínűség számolásához ismernünk kellene a paramétereket. Ezen az önmagába visszakanyarodó problámán úgy tudunk úrrá lenni, hogy veszünk egy kiindulási paramétert, amivel elvégezzük a számolást, majd az így kapott új paraméterekkel megismételjük, amíg a paraméterértékek állandósulnak. Ez az EM algoritmus. A konvergenciát az EM algoritmus tétel biztosítja.
A keverék eloszlásból vett független ![]() elemszámú megfigyelhető mintát jelölje
elemszámú megfigyelhető mintát jelölje
ami a koponyákon mért értékek sorozata.
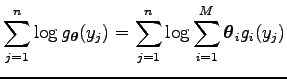
Ezt differenciálva a
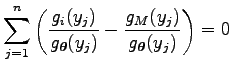
likelihood egyenletet kapjuk, ami általános esetben nehezen oldható meg a paraméterekre.
Ahhoz, hogy hiányos adat problémaként kezelhessük a feladatot vezessük be a hiányzó, illetve rejtett
adatrendszert, ahol
Ha a ![]() változók megfigyelhetőek lennének, akkor
változók megfigyelhetőek lennének, akkor
![]() becslése egyszerűen
becslése egyszerűen
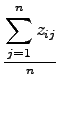
volna, ami a sűrűség
A teljes adatrendszer log likelihoodja polinomiális alakú:
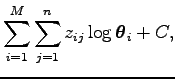
ahol
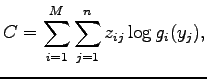
ami nem függ a paraméterektől. Mivel ez a kifejezés lineáris
Láttuk korábban, hogy minden esetben, amikor a két változónak van sűrűségfüggvénye, akkor a feltételes várható értéket az együttes sűrűségfüggvény és a feltételben álló változó marginális sűrűségfüggvényének hányadosa szerint kell venni. Az együttes sűrűségfüggvény a
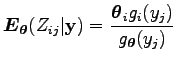
Ez tulajdonképpen a Bayes tétel sűrűségfüggvényekre vonatkozó alakja, mert
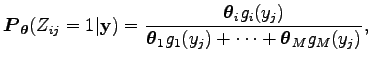
vagy feltételes sűrűségfüggvényekkel kifejezve
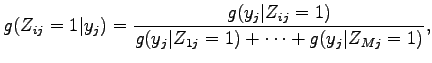
mert az előző egyenletben a bal oldal csak az
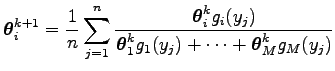
egyenlet definiálja.
Az EM algoritmus tétel biztosítja a konvergenciát a hiányos adatrendszer likelihoodjának egy
stacionárius pontjához, de ebben az esetben be is bizonyítható, hogy az EM algoritmus tényleg
a likelihood egyenlet megoldásához konvergál.
Ha
![]() a likelihood egyenlet megoldása, akkor a paraméter helyébe a
a likelihood egyenlet megoldása, akkor a paraméter helyébe a
![]() paramétert
helyettesítve és a likelihood egyenlet mindkét oldalát beszorozva
paramétert
helyettesítve és a likelihood egyenlet mindkét oldalát beszorozva
![]() paraméterrel, ahol az
paraméterrel, ahol az ![]() index
index ![]() és
és ![]() között változik, akkor a
között változik, akkor a
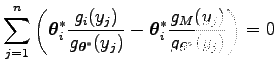
egyenletet kapjuk. Az egyenlet
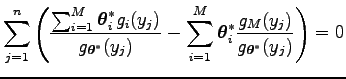
egyenletre vezet. Azaz
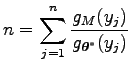
Ezt visszahelyettesítve az első egyenletbe, azt kapjuk, hogy
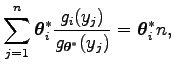
ami azt jelenti, hogy
További részletek és numerikus példa található a [4] könyvben.
Temesi Róbert 2010-08-16