Next: Keverék eloszlások Up: Az EM algoritmus Previous: EM algoritmus konvergenciája Tartalomjegyzék
Az EM cikk szerzői is ezt a példát említik elsőként.
A hiányos adatrendszerhez tartozó
![]() mintatér legyen olyan
mintatér legyen olyan ![]() dimenziós nemnegatív egész értékű
vektorok halmaza, amelyben a koordináták összege konstans, például
dimenziós nemnegatív egész értékű
vektorok halmaza, amelyben a koordináták összege konstans, például ![]()
![]() álljon
álljon
![]() összes
lehetséges
részhalmazából, azaz
összes
lehetséges
részhalmazából, azaz
![]() Legyen
Legyen ![]() a számláló mérték, azaz az egyelemű halmazok
mértéke legyen
a számláló mérték, azaz az egyelemű halmazok
mértéke legyen ![]() , a véges halmazok mértéke legyen annyi, ahány elemet tartalmaz, a végtelen halmazok
mértéke legyen
, a véges halmazok mértéke legyen annyi, ahány elemet tartalmaz, a végtelen halmazok
mértéke legyen ![]() Ekkor a
Ekkor a
![]() sűrűségfüggvény egy
sűrűségfüggvény egy
![]() ponton megegyezik a
ponton megegyezik a
![]() valószínűséggel. Legyen a
valószínűséggel. Legyen a
![]() paramétertér a
paramétertér a ![]() nyílt intervallum.
Egy
nyílt intervallum.
Egy
![]() valószínűsége
legyen
valószínűsége
legyen
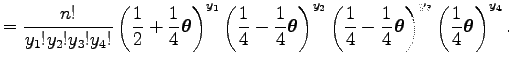
Tehát az eloszlás egy multinomiális eloszlás az
Nem szükséges EM algoritmus a paraméterbecsléshez, amennyiben maximum likelihood módszerrel akarjuk becsülni a paramétert egy konkrét mintából. A maximum likelihood egyenlet explicite megoldható ebben az esetben. Rövidítse a
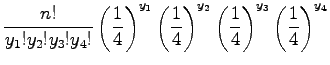
kifejezést
A log likelihood függvény
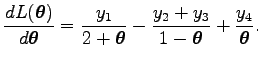
A
egyenletre vezet. Mivel a log likelihood függvény második deriváltjának mínusz egyszerese
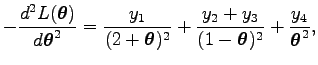
ezért nem negatív
Noha létezik explicit megoldás, mégis érdemes megnézni az EM algoritmust ezen a példán, mert itt jól nyomon követhető az algoritmus működése, valamint több dimenziós hiányos adatrendszer esetén már nem lehet explicite megoldani a log likelihood egyenletet, mert az egy magasabbfokú polinom gyökeinek megkeresésére vezet.
Ezt a multinomiális mintát úgy is produkálhatjuk, hogy egymástól függetlenül ![]() alkalommal veszünk
egy 4 dimenziós indikátor változóból mintát úgy, hogy az indikátor változó komponenseiben az egyesek
valószínűsége a multinomiális eloszlás paramétereinek felel meg, majd összeszámoljuk, hogy az
indikátor változó melyik értéke hányszor jött ki, illetve összegezhetjük is az indikátor változókat.
Fogalmazhatjuk ezt úgy is, hogy van négy urnánk és ezekbe rendre a multinomiális eloszlás
paramétereinek valószínűségével esik egy golyó. Tehát az elsőbe
alkalommal veszünk
egy 4 dimenziós indikátor változóból mintát úgy, hogy az indikátor változó komponenseiben az egyesek
valószínűsége a multinomiális eloszlás paramétereinek felel meg, majd összeszámoljuk, hogy az
indikátor változó melyik értéke hányszor jött ki, illetve összegezhetjük is az indikátor változókat.
Fogalmazhatjuk ezt úgy is, hogy van négy urnánk és ezekbe rendre a multinomiális eloszlás
paramétereinek valószínűségével esik egy golyó. Tehát az elsőbe
![]() , a
másodikba és a harmadikba
, a
másodikba és a harmadikba
![]() , a negyedikbe
, a negyedikbe
![]() valószínűséggel esik golyó.
valószínűséggel esik golyó.
Úgy is elképzelhetjük ezt a szituációt, hogy az első urnát kettévalasztjuk, és úgy gondolunk rá,
mintha az egyik részbe konstans ![]() valószínűséggel esne golyó, a másikba pedig
valószínűséggel esne golyó, a másikba pedig
![]() valószínűséggel esne golyó. Ha tudnánk, hogy az első urna képzeletbeli rekeszeibe
a mintavételezés során hány golyó esett, akkor egyszerűen meghatározhatnánk a paraméter maximum
likelihood becslését, hiszen ekkor kis átalakítással a binomiális eloszlás paraméterének ismert
maximum likelihood becslésére vezethetnénk vissza a problémát. Nem ismerjük a problémát
leegyszerűsítő rekesz darabszámokat, ezért mondhatjuk, hogy az eredeti minta egy hiányos adatrendszer.
Mivel nem ismerjük, hogy az első
urna melyik rekeszébe hány golyó esik, ezért a számolások során csak az ismert golyószámok melletti
feltételes várható értékét vehetjük az első urna rekeszeibe eső golyók számának. Az EM algoritmus
során fellépő számolásokban a hiányzó golyószámokat lehet helyettesíteni azok feltételes várható
értékével. Ez általánosságban nem tehető meg, hanem a log likelihood függvény feltételes várható
értékét kell venni.
valószínűséggel esne golyó. Ha tudnánk, hogy az első urna képzeletbeli rekeszeibe
a mintavételezés során hány golyó esett, akkor egyszerűen meghatározhatnánk a paraméter maximum
likelihood becslését, hiszen ekkor kis átalakítással a binomiális eloszlás paraméterének ismert
maximum likelihood becslésére vezethetnénk vissza a problémát. Nem ismerjük a problémát
leegyszerűsítő rekesz darabszámokat, ezért mondhatjuk, hogy az eredeti minta egy hiányos adatrendszer.
Mivel nem ismerjük, hogy az első
urna melyik rekeszébe hány golyó esik, ezért a számolások során csak az ismert golyószámok melletti
feltételes várható értékét vehetjük az első urna rekeszeibe eső golyók számának. Az EM algoritmus
során fellépő számolásokban a hiányzó golyószámokat lehet helyettesíteni azok feltételes várható
értékével. Ez általánosságban nem tehető meg, hanem a log likelihood függvény feltételes várható
értékét kell venni.
A teljes adatrendszerhez tartozó
![]() mintatér tehát legyen az olyan 5 dimenziós nem negatív
értékeket tartalmazó vektorok halmaza, melyekben a komponensek összege
mintatér tehát legyen az olyan 5 dimenziós nem negatív
értékeket tartalmazó vektorok halmaza, melyekben a komponensek összege ![]() A mérhető halmazok
összessége,
A mérhető halmazok
összessége,
![]() legyen az összes részhalmazok halmaza,
legyen az összes részhalmazok halmaza,
![]() A
A ![]() mérték legyen a számláló mérték, mint a hiányos adatrendszer esetén.
Így az
mérték legyen a számláló mérték, mint a hiányos adatrendszer esetén.
Így az ![]() sűrűségfüggvény most is megegyezik a valószínűséggel, és tetszőleges
sűrűségfüggvény most is megegyezik a valószínűséggel, és tetszőleges
![]() vektorra legyen
vektorra legyen
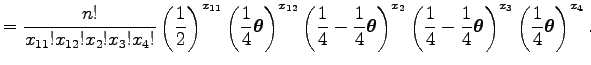
A
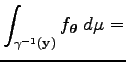
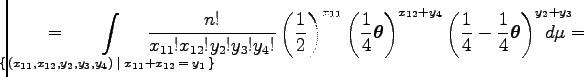
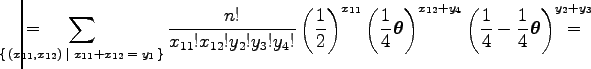
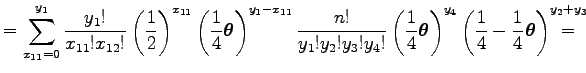
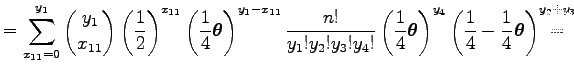
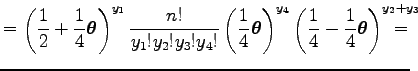
A
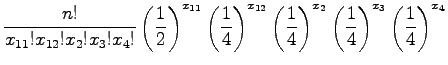
kifejezést jelölje
Az egyenlőség utolsó elemének első tagja egy
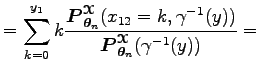
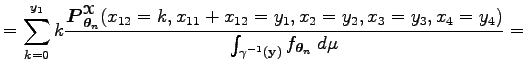
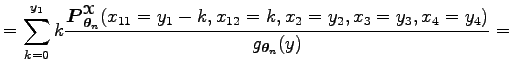
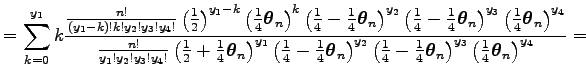
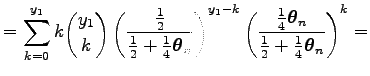
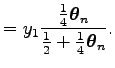
Ugyanis a legutolsó összeg egy
Összegezve, a maximalizálandó
![]() feltételes várható érték
feltételes várható érték
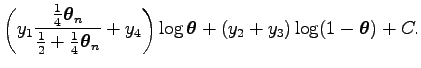
Ez a függvény a
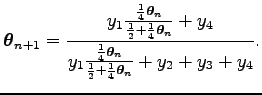
Az EM algoritmus konvergenciája tétel miatt a
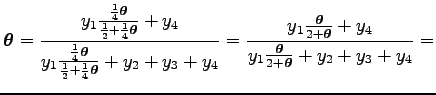
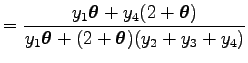
Az egyenlet elejéből és végéből átrendezéssel adódik a
egyenlet.
Temesi Róbert 2010-08-16