EM algoritmus konvergenciája

Sokszor a likelihood függvényt nehéz maximalizálni, vagy nem is lehet a megoldást felírni zárt alakban. Ekkor numerikus módszerekre van szükség. Sok esetben kézenfekvően tekinthetünk úgy a mintára, mint egy bővebb mintának egy látható részére, ahol ez a bővebb minta olyan statisztikai mezőből származik, amiben könnyű maximalizálni a likelihood függvényt. A gond az, hogy ennek a bővebb mintának csak egy részét, az eredeti mintát ismerjük. Ezt úgy lehet megoldani, hogy a hiányzó rész eredeti minta szerinti feltételes várható értékét vesszük valamilyen kiindulási paraméter választással a bővebb minta likelihoodjának maximalizálása során. Így bizonyíthatóan jobb paramétert kapunk, vagyis ezzel a paraméterrel az eredeti likelihood értéke az eredeti mintában nagyobb, illetve nem kisebb, mint a kiindulási paraméterrel volt. Ezt az eljárást folytatva az új paraméterrel, majd tovább iterálva lépésenként jobb, és az eredeti likelihood egyenlet megoldásához konvergáló, paraméterek sorozatát kapjuk, ha az eredeti likelihoodnak egyetlen stacionárius pontja van. A bővebb mintát hívjuk teljes adatrendszernek, annak látható részét pedig hiányos adatrendszernek.

Tétel 2   EM algoritmus konvergenciája
Legyen $(\boldsymbol{\EuScript X},\boldsymbol{\EuScript A}, \{\boldsymbol P_{\boldsymb... ...eta }^{\boldsymbol{\EuScript X}}\vert\boldsymbol\theta \in\boldsymbol\Theta \})$ és $(\boldsymbol{\EuScript Y},\boldsymbol{\EuScript B}, \{\boldsymbol P_{\boldsymb... ...eta }^{\boldsymbol{\EuScript Y}}\vert\boldsymbol\theta \in\boldsymbol\Theta \})$ statisztikai mezők $f_{\boldsymbol\theta }$ és $g_{\boldsymbol\theta }$ $\mu$ és $\nu$ mérték szerinti sűrűségfüggvényekkel. Legyen $\gamma : \boldsymbol{\EuScript X} \rightarrow \boldsymbol{\EuScript Y}$ függvény úgy, hogy a sűrűségfüggvényekkel tetszőleges $y \in \boldsymbol{\EuScript Y}$ elemre teljesüljön a

$$g_{\boldsymbol\theta }(y) = \int_{\gamma^{-1}(y)} f_{\boldsymbol\theta }\;d\mu$$

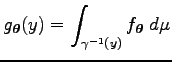
egyenlőség. Ekkor tetszőleges $\boldsymbol\theta _0\in\boldsymbol\Theta$ kiindulási paraméter és $y \in \boldsymbol{\EuScript Y}$ esetén az $\boldsymbol E_{\boldsymbol\theta _n}(\log f_{\boldsymbol\theta }\vert\gamma^{-1}(y))$ értéket a $\boldsymbol\theta$ paraméterben maximalizáló $\boldsymbol\theta _{n+1}$ paraméterek sorozata konvergens, a $g_{\boldsymbol\theta _n}(y)$ értékek pedig monoton nem csökkenő sorozatot alkotnak.