Next: 1. IBM modell másképp Up: Az IBM modellek Previous: Az IBM modellek Tartalomjegyzék
Legyen
![]() a lehetséges angol szavak halmaza,
a lehetséges angol szavak halmaza,
![]() pedig a lehetséges
francia szavak halmaza, mindkettő véges. Legyen
pedig a lehetséges
francia szavak halmaza, mindkettő véges. Legyen ![]() és
és ![]() a leghosszabb angol, illetve francia
mondat hossza. Formálisan minden mondat
a leghosszabb angol, illetve francia
mondat hossza. Formálisan minden mondat ![]() illetve
illetve ![]() hosszú lesz, az egységes írásmód kedvéért,
a nem elég hosszú mondatokat kiegészítjük
hosszú lesz, az egységes írásmód kedvéért,
a nem elég hosszú mondatokat kiegészítjük ![]() jelekkel. Tehát
jelekkel. Tehát ![]() és
és ![]() angol,
illetve francia mondathalmazra teljesül, hogy
angol,
illetve francia mondathalmazra teljesül, hogy
![]() és
és
![]() Minden angol illetve francia
Minden angol illetve francia ![]() és
és ![]() mondathoz hozzárendelhetjük a tényleges hosszát,
az
mondathoz hozzárendelhetjük a tényleges hosszát,
az ![]() és
és ![]() hosszakat.
Legyen
hosszakat.
Legyen ![]() az
az ![]() dimenziójú
dimenziójú ![]() mátrixok halmaza.
Legyen
mátrixok halmaza.
Legyen
![]() a lehetséges fordítások halmaza, és rendelkezzen azzal a
tulajdonsággal, hogy
a lehetséges fordítások halmaza, és rendelkezzen azzal a
tulajdonsággal, hogy
![]() esetén
esetén
![]() valamint
valamint
![]() , ha
, ha
![]() vagy
vagy
![]() A feltételek azt jelentik, hogy az
A feltételek azt jelentik, hogy az ![]() mátrix soraiban egyetlen egyes található,
a többi 0
, valamint 0
van azokon a helyeken, ahol valamelyik mondatban nincs tényleges szó,
azaz ahol formálisan
mátrix soraiban egyetlen egyes található,
a többi 0
, valamint 0
van azokon a helyeken, ahol valamelyik mondatban nincs tényleges szó,
azaz ahol formálisan ![]() található.
Az
található.
Az ![]() mátrixot úgy interpretáljuk hogy akkor áll
mátrixot úgy interpretáljuk hogy akkor áll ![]() az
az ![]() helyen,
ha az
helyen,
ha az ![]() -edik francia szó, azaz
-edik francia szó, azaz ![]() a
a ![]() -edik angol szóból, azaz az
-edik angol szóból, azaz az ![]() szóból származik,
vagyis annak a fordítása. Az
szóból származik,
vagyis annak a fordítása. Az ![]() -edik sor tehát az
-edik sor tehát az ![]()
![]() -edik francia szóhoz tartozik és
egy indikátor vektor, mely megmutatja, hogy melyik angol szóból származik, és annak sorszámánál
áll egy egyes.
Tehát azt követeljük meg, hogy egy francia szó egyetlen angol szóból származhasson, és a francia mondat
végén levő
-edik francia szóhoz tartozik és
egy indikátor vektor, mely megmutatja, hogy melyik angol szóból származik, és annak sorszámánál
áll egy egyes.
Tehát azt követeljük meg, hogy egy francia szó egyetlen angol szóból származhasson, és a francia mondat
végén levő ![]() szavak ne származzanak angol szóból, valamint a francia szavak ne származzanak
az
szavak ne származzanak angol szóból, valamint a francia szavak ne származzanak
az ![]() szóból.
szóból.
A teljes adatrendszerhez tartozó
![]() mintatér, amit teljes mintatérnek is nevezünk, a
mintatér, amit teljes mintatérnek is nevezünk, a
![]() térből vett
térből vett ![]() darab független mintát reprezentál, ezért
darab független mintát reprezentál, ezért
![]() Az
Az
![]() térhez tartozó statisztikai mező
térhez tartozó statisztikai mező
![]() ,
ahol tetszőleges
,
ahol tetszőleges
![]() teljes mintára
teljes mintára
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
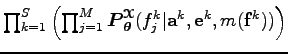
![]()
![]()
![]()
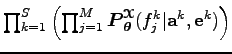
![]()
![]()
![]()
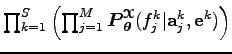
![]()
![]()
![]()
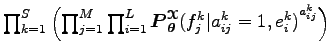
![]()
![]()
![]()
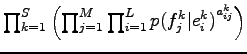
![]()
![]()
![]()
Az EM algoritmusban szereplő
![]() és
és
![]() mérték a számláló mérték lesz a megfelelő mérhető
tereken,
ezért az
mérték a számláló mérték lesz a megfelelő mérhető
tereken,
ezért az
![]() sűrűség megegyezik a
sűrűség megegyezik a
![]() valószínűséggel.
Ez a valószínűség szorzatra bomlik, mert angol mondat
valószínűséggel.
Ez a valószínűség szorzatra bomlik, mert angol mondat ![]() alignment
alignment ![]() francia mondat hármasonként
függetlenséget szeretnénk. Ezeket a szorzótényezőket a lánc szabály segítségével tovább írjuk.
Egy adott francia mondat, feltéve a hozzá tartozó alignmentet, angol mondatot és mondathosszt,
független módon áll össze a szavaiból, ezért egy francia mondat valószínűsége a szavai
valószínűségeinek szorzatára bomlik. A feltételből elhagyható a mondathosszhoz tartozó esemény, mert
ez bővebb esemény, mint az adott alignmenthez tartozó esemény. Továbbá egy francia mondatban egy
adott szó és annak valószínűsége csak az alignment hozzá tartozó sorától függ, a többitől nem.
A
francia mondat hármasonként
függetlenséget szeretnénk. Ezeket a szorzótényezőket a lánc szabály segítségével tovább írjuk.
Egy adott francia mondat, feltéve a hozzá tartozó alignmentet, angol mondatot és mondathosszt,
független módon áll össze a szavaiból, ezért egy francia mondat valószínűsége a szavai
valószínűségeinek szorzatára bomlik. A feltételből elhagyható a mondathosszhoz tartozó esemény, mert
ez bővebb esemény, mint az adott alignmenthez tartozó esemény. Továbbá egy francia mondatban egy
adott szó és annak valószínűsége csak az alignment hozzá tartozó sorától függ, a többitől nem.
A ![]() -adik francia mondat
-adik francia mondat ![]() -edik szava,
-edik szava, ![]() csak a
csak a ![]() -adik angol mondat
-adik angol mondat ![]() -edik szavától,
-edik szavától,
![]() szótól függ, ha
szótól függ, ha
![]() , tehát minden francia szó csak egy angol szóból származik,
ezért a
, tehát minden francia szó csak egy angol szóból származik,
ezért a
![]() valószínűség
valószínűség
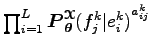 alakban fejezhető ki, mert
ebből a szorzatból csak az a tényező nem egy, amelyik indexére
alakban fejezhető ki, mert
ebből a szorzatból csak az a tényező nem egy, amelyik indexére
![]() Ugyanis a
Ugyanis a ![]() kifejezést definíció szerint
kifejezést definíció szerint ![]() -nek tekintjük.
A
-nek tekintjük.
A
![]() értékeket ismertnek tételezzük fel.
Legyen minden francia mondathossz egyenlő valószínűségű, ezért
értékeket ismertnek tételezzük fel.
Legyen minden francia mondathossz egyenlő valószínűségű, ezért
![]() Szintén tételezzünk fel egyformán
valószínűnek minden adott angol mondathosszhoz, és adott francia mondathosszhoz tartozó alignmentet,
ezért
Szintén tételezzünk fel egyformán
valószínűnek minden adott angol mondathosszhoz, és adott francia mondathosszhoz tartozó alignmentet,
ezért
![]()
![]()
![]() A
A
![]() valószínűségeket tekintsük a
valószínűségeket tekintsük a
![]() jellel
jelölt paramétereknek.
A fenti egyenletekben tetszőleges
jellel
jelölt paramétereknek.
A fenti egyenletekben tetszőleges
![]() esetén
esetén
![]() és
és
![]() , valamint
, valamint
![]() és
és
![]() esetén
esetén
![]()
![]()
![]()
A
![]() paraméter halmaz álljon olyan vektorokból, melynek koordinátáit az
paraméter halmaz álljon olyan vektorokból, melynek koordinátáit az
![]() halmaz elemeivel indexeljük, az
halmaz elemeivel indexeljük, az ![]() elemmel
indexelt helyen
elemmel
indexelt helyen ![]() áll, és
áll, és
![]() , valamint
, valamint
![]() szóra
szóra
![]() A
A ![]() paramétereket kell tehát becsülni.
paramétereket kell tehát becsülni.
A hiányos adatrendszerhez tartozó mintatér elemei legyenek a teljes adatrendszerhez tartozó mintatér
elemei elhagyva belőlük az alignmenteket. Tehát
![]() és
a
és
a
![]() függvényre pedig teljesül
függvényre pedig teljesül
![]()
![]()
![]() A hiányos adatrendszerhez tartozó statisztikai mező pedig legyen
A hiányos adatrendszerhez tartozó statisztikai mező pedig legyen
![]() Az
Az
![]() elemeknek a valószínűségét csak úgy tudjuk definiálni, hogy összegezzük azoknak az
elemeknek a valószínűségét csak úgy tudjuk definiálni, hogy összegezzük azoknak az
![]() elemeknek a valószínűségét, melyek az
elemeknek a valószínűségét, melyek az ![]() mögött állhatnak.
Így az EM algoritmus konvergenciájáról szóló tételben álló, a sűrűségekre vonatkozó, feltétel
automatikusan teljesül, mert a sűrűségekhez tekintett mérték a számláló mérték a megfelelő tereken, és
ezért az
mögött állhatnak.
Így az EM algoritmus konvergenciájáról szóló tételben álló, a sűrűségekre vonatkozó, feltétel
automatikusan teljesül, mert a sűrűségekhez tekintett mérték a számláló mérték a megfelelő tereken, és
ezért az
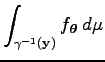
integrál átmegy a
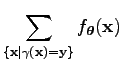
összegbe. Azaz
elemre
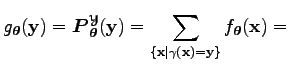
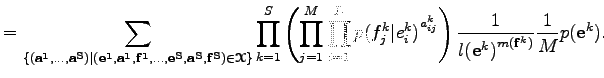
Az összegzés csak azokra az alignemntekre történik, melyek a megadott mondatokhoz hozzátartozhatnak, azaz csak olyan helyen áll bennük egyes, amely helyek a mondatok tényleges hossza által adott index-határokon belül vannak.
A
![]() paraméterben maximalizálandó feltételes várható érték
paraméterben maximalizálandó feltételes várható érték
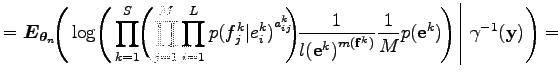
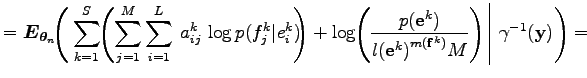
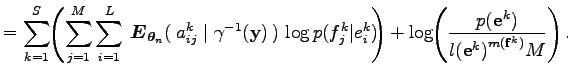
Az egyenlőség első három sorában a várható értékben szereplő mennyiségek függnek az
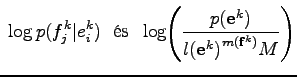
mennyiségek viszont csak
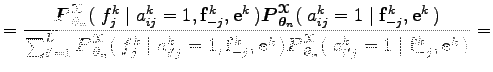
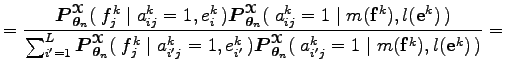
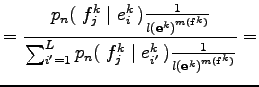
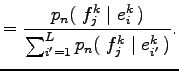
Ahol a
Az
![]() feltételes várható értékre vezessük be az
feltételes várható értékre vezessük be az
![]() jelölést. A
jelölést. A
![]() és
és
![]() halmazokon egyaránt jelölje
halmazokon egyaránt jelölje ![]() a Kronecker delta
függvényt. Azaz
a Kronecker delta
függvényt. Azaz
![]() ha
ha ![]() . egyébként
. egyébként ![]() Ezután maximalizáljuk az
Ezután maximalizáljuk az
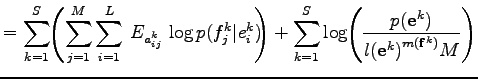
feltételes várható értéket a paraméterekben. A második tag a paraméterekben konstans, ezért el is hagyhatjuk a maximalizálás során. Mivel minden lehetséges
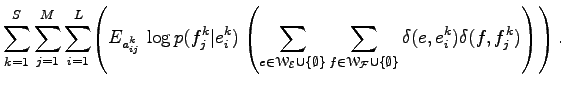
Mivel
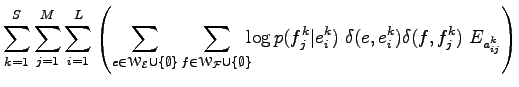
összeget kapjuk. A
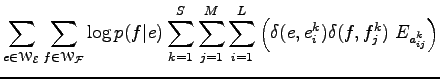
Az összegzésből az üres halmazok elhagyhatóak, mert több okból is nullával járulnak hozzá az összeghez. Ha az első szumma szerint bontjuk tagokra az összeget, akkor a
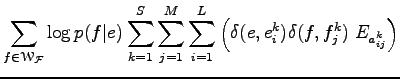
tagok csak egy konkrét
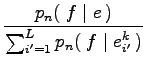
kifejezést adja amikor a Kronecker delta függvények egyet adnak, ezért kicserélhető erre a kifejezésre. Tehát tetszőleges
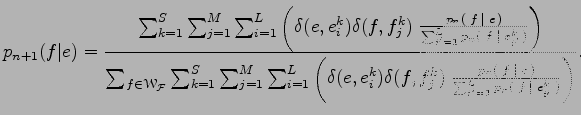
Ez a képlet azt mondja el, hogy úgy kell kiszámolni egy adott francia, és egy adott angol szó újabb valószínűségét, hogy azokban a mondatpárokban, amelyekben előfordulnak ezek a szavak meg kell nézni a francia szó minden előfordulására, hogy a korábbi fordítási valószínűségének mennyi a relatív súlya az angol mondat összes szavának a franciára való fordítási valószínűségei között, majd ezeket a relatív súlyokat összegezni kell az egész szöveg beli összes előfordulásra, és az így kapott mennyiséget normálni kell az adott angol szó összes francia fordításának valószínűségei között.
Temesi Róbert 2010-08-16