Next: 2. IBM modell Up: Az IBM modellek Previous: 1. IBM modell Tartalomjegyzék
Az 1. IBM modellt bevezető cikkben [1] másfajta tárgyalást használnak, minél elemibb matematikai
eszközökkel szeretnék levezetni a paraméterbecslés formuláját, és sokat támaszkodnak a szemléletre.
Ezért matematikai szempontból a szerzők nem elég pontosan járnak el. Mégis tanulságos megnézni ezt
a levezetést, mert lényegében ugyanazt az eredményt kapják, amit fent levezettem, és algoritmikus
szempontból ugyanazt kell csinálni a számítógéppel való számoláskor. Elemibb eszközöket használnak
a formulák kiszámításához, de mégis kerülőúton jutnak arra az eredményre, amire én a tétel közvetlen
alkalmazásával. Tehát láthatjuk, hogy sok esetben a hiányos adatrendszer likelihood függvénye
közvetlenül is maximalizálható, de ekkor semmi sem garantálja a felírt iteratív eljárás
konvergenciáját. Illetve ekkor a konvergencia külön megfontolás tárgya, vagy ha könnyen kipróbálható
az algoritmus a valóságban, számítógépen, akkor lehet vele kísérletezni. Ez a szokásos mérnöki
megközelítés. Tehát szerzők jelöléseikkel élve egy
![]() francia, egy
francia, egy ![]() alignment és egy
alignment és egy ![]() angol mondat valószínűségét a következő
alakban írják fel:
angol mondat valószínűségét a következő
alakban írják fel:
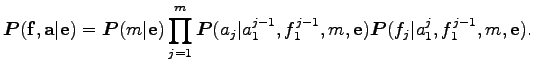
Itt
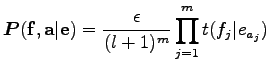
formulát kapják. Egy mondatpár fordítási valószínűségét a lehetséges alignmentekre összegezve kapjuk. Ezért
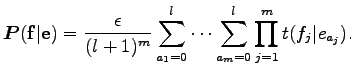
Tehát a feladatunk az, hogy a
A probléma direkt megoldásához bevezetve a ![]() Lagrange multiplikátorokat a feltételes
szélsőérték keresésére a
Lagrange multiplikátorokat a feltételes
szélsőérték keresésére a
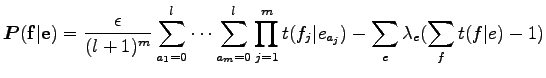
kifejezést kell maximalizálnunk, most már a paraméterekben és a
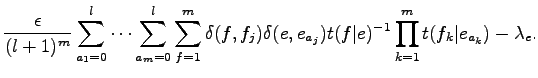
Ahol
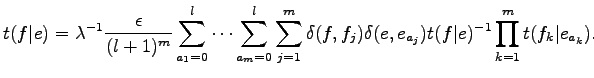
Ez a felírás azt sugallja, hogy érdemes egy iteratív eljárást alkalmazni az egyenlet megoldására. A cikk irói azt állítják, hogy ez egy EM algoritmusra vezet, ám nem bizonyítják. A korábbi formulák segítségével és az egymásba ágyazott összegeket a teljes alignmenteken való egyetlen összegnek írva a
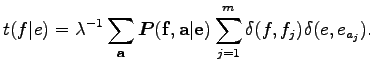
Ebben az egyenletben a Kronecker delta függvények szorzatát tartalmazó összeg megadja, hogy
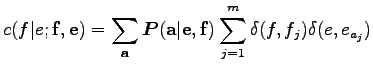
Mivel a
A gyakorlatban azonban több mondatpár is rendelkezésünkre áll, ezért
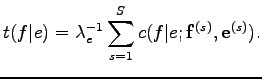
Ez az egyenlet megfelel az M lépésnek. Ugyanis, ha a bal oldalon álló paramétert a jobboldalon állók függvényeként akarjuk kiszámolni, vagyis veszünk kiindulási paramétereket, majd ezeket a jobb oldalba helyettesítjük, és a bal oldalon megjelenő értékeket tekintjük az új paramétereknek, akkor láthatjuk, hogy a régi paraméterekkel vett
Most térjünk rá a feltételes várható érték paraméterek szerinti kiszámolására, hiszen eddig csak
felírtuk azt a feltételes valószínűségekkel. Tulajdonképpen elvileg ebben a fázisban is ki tudnánk
számolni a
![]() valószínűségeket, hiszen ez
valószínűségeket, hiszen ez
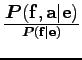
és ezeknek pedig ismerjük a paraméterekkel való felírását. Az egyetlen probléma, hogy a nevezőben az összes lehetséges alignmentre összegezni kell, ami a gyakorlatban kivitelezhetetlen. Ezért az abban szereplő összegzésre tekintsük a következő azonosságot:
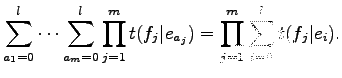
Ennek a kifejezésnek a segítségével a nevező a következő alakban írható:
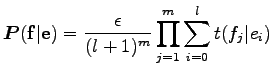
Így a
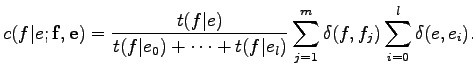
Lényegében tehát a Bayes-tételt alkalmazzuk, ami előzőleg is kijött. Ezzel a kis trükkel megoldottuk, hogy az
Temesi Róbert 2010-08-16