2. IBM modell

Az IBM cikkben [1] további modelleket is fellállítanak. A 2. modellt röviden ismertetem. Ez csak annyiban különbözik az elsőtől, hogy a $\boldsymbol P(a_j\vert a_1^{j-1},f_1^{j-1},m,{\bf e})$ valószínűségekről azt teszik fel, hogy csak $j$ -től, $a_j$ -től, $m$ -től és $l$ -től függ, és ezt a valószínűséget is paraméternek tekintik.

$$a(a_j\vert j,m,l)=\boldsymbol P(a_j\vert a_1^{j-1},f_1^{j-1},m,{\bf e}),$$

ahol a paraméter kielégiti a

$$\sum_{i=0}^l a(a_j\vert j,m,l)=1$$

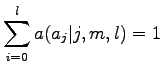
feltételt. Ezzel az új paraméterrel együtt kifejezve a $\boldsymbol P({\bf f}\vert{\bf e})$ a

$$\boldsymbol P({\bf f}\vert{\bf e})=\epsilon\sum_{a_1=0}^l\cdots\sum_{a_m=0}^l \prod_{j=1}^m t(f_j\vert e_{a_j})a(a_j\vert j,m,l)$$

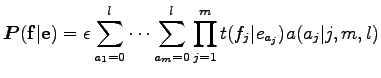
alakban írható. A $\lambda$ és $\mu$ Lagrange multiplikátorokat bevezetve a

$\boldsymbol P({\bf f}\vert{\bf e})=\epsilon\sum_{a_1=0}^l\cdots\sum_{a_m=0}^l \prod_{j=1}^m t(f_j\vert e_{a_j})a(a_j\vert j,m,l)-$

$-\sum_e \lambda_e(\sum_f t(f\vert e)-1)-\sum_j\mu_{jml}(\sum_ia(i\vert j,m,l)-1)$

kifejezést kell maximalizálni a paraméterekben, $\lambda$ -ban és $\mu$ -ben. Jelöljük az $i$ index feltételes várható értékét $c(i\vert j,m,l,{\bf f},{\bf e})$ -vel, azaz

$$c(i\vert j,m,l,{\bf f},{\bf e})=\sum_a\boldsymbol P({\bf a}\vert{\bf e},{\bf f})\delta(i,a_j.)$$

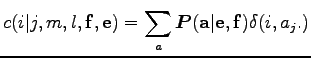
Ezzel a jelöléssel a teljes mintát figyelembe véve

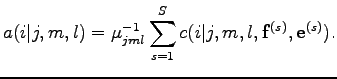
$$a(i\vert j,m,l)=\mu_{jml}^{-1}\sum_{s=1}^Sc(i\vert j,m,l,{\bf f}^{(s)},{\bf e}^{(s)}).$$

A $\boldsymbol P({\bf f}\vert{\bf e})$ paraméterekkel való kifejezésében az összegzés és a produktum most is felcsrélhető egymással, mint az 1. modell esetében.

$$\boldsymbol P({\bf f}\vert{\bf e})=\epsilon\prod_{j=1}^m\sum_{i=0}^lt(f_j\vert e_i)a(i\vert j,m,l).$$

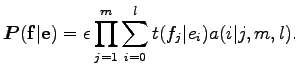
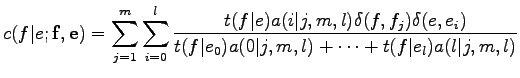
Ezeket a kifejezéseket használva, a Bayes tétellel a háttérben a $c$ feltételes várható értékekre a következőket kapjuk:

$$c(f\vert e;{\bf f},{\bf e})=\sum_{j=1}^m\sum_{i=0}^l{{t(f\vert e)... ..._i)} \over{t(f\vert e_0)a(0\vert j,m,l)+\cdots +t(f\vert e_l)a(l\vert j,m,l)}}$$

és

$$c(i\vert j,m,l,{\bf f},{\bf e})={{t(f_j\vert e_i)a(i\vert j,m,l)} \over{t(f_j\vert e_0)a(0\vert j,m,l)+\cdots +t(f_j\vert e_l)a(l\vert j,m,l)}}$$

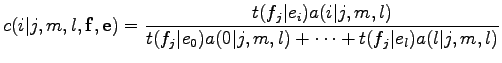
A fenti két képletbe behelyettesítve a régi $t$ és $a$ paramétereket, megkaphatjuk az új paramétereket, $t$ esetében az 1. modell szerinti képlettel, amihez képest csak annyi a változás, hogy a várható értékben figyelembe vesszük $a$ értékeit is, $a$ számolásakor pedig a második képletet használhatjuk.