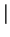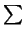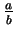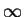


Next: A természetes nyelvek kezelése
Up: A matematikai mód
Previous: Elemi függvények Maclaurin sorai
Tartalomjegyzék
Ugyan nem célom a TEXnikai részleteket tárgyalni, mégis, az elvek
szempontjából is fontosnak érzem, hogy néhány dolgot elmagyarázzak az
alábbi forráskód részletből, ami LATEX nyelven készült. Amit most
írok, csak első közelítésben igaz, a TEX nagyon rugalmasan
programozható.
A TEX-es parancsokat a
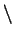 jel vezeti be. A kötelező
paramétereik a {} zárójelpár között vannak, míg az opcionálisokat a
zárójelpár tartalmazza. A {} pár használandó még a blokkok
kijelölésére, a közte lévő karaktereket sok szempontból egy egységként
kezeli a TEX. Egy ilyen pár természetesen tartalmazhat további
parancsokat és {} párokat is.
A TEX-nek alapvetően két üzemmódja van, a szöveges és a
matematikai. A dokumentum matematikát tartalmazó részei vannak a mat
módban. Ebbe kapcsolni a
jel vezeti be. A kötelező
paramétereik a {} zárójelpár között vannak, míg az opcionálisokat a
zárójelpár tartalmazza. A {} pár használandó még a blokkok
kijelölésére, a közte lévő karaktereket sok szempontból egy egységként
kezeli a TEX. Egy ilyen pár természetesen tartalmazhat további
parancsokat és {} párokat is.
A TEX-nek alapvetően két üzemmódja van, a szöveges és a
matematikai. A dokumentum matematikát tartalmazó részei vannak a mat
módban. Ebbe kapcsolni a \( vagy a \[ parancsokkal
lehet, visszakapcsolni a szövegesbe a \) vagy a \]
utasításokkal. A kettő közül a \( a szövegközi mat mód, míg a
\[ a kiemelt mód.
Néhány itt használt LATEX parancs:
| _ |
alsó index |
| ^ |
felső index |
\vert |
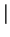 |
\sum |
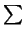 |
\frac{a}{b} |
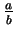 |
\infty |
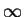 |
\begin{itemize}
\item általános alak:
\begin{equation}
\sum_{n=0}^{\infty}c_{n}x^{n} \label{eq:sor}
\end{equation}
\item a \ref{eq:sor} hatványsor konvergenciasugara
\[r = \frac{1}{\varlimsup \sqrt[n]{\vert c_{n} \vert}},\]
amennyiben
\[\varlimsup \sqrt[n]{\vert c_{n} \vert}
\left\{
\begin{array}{ll}
=\infty & \mbox{akkor} \;r=0\\
=0 & \mbox{akkor} \; r=\infty
\end{array}
\right. \]
\end{itemize}
\subsection*{Elemi függvények Maclaurin sorai}
\begin{itemize}
\item $ \ln {(1+x)}=\sum_{k=0}^{\infty}
\frac{(-1)^{k}x^{k+1}}{k+1}, \enskip x \in (-1,1)$
\item $ \sh {x}=\sum_{k=0}^{\infty} \frac{x^{2k+1}}{(2k+1)!},
\enskip x \in (-\infty, +\infty)$
\end{itemize}
\begin{lemma}[Riemann-Lebesgue]
legyen az $f$ függvény az $[a,b]$ intervallumban véges
számú hely kivételével folytonos és szakadási helyein
legyen elsőfajú szakadása, ekkor
\[\lim_{\lambda \rightarrow \infty}\int_{a}^{b}f(x)\cos{\lambda
x}\mathrm{d}x=\lim_{\lambda \rightarrow
\infty}\int_{a}^{b}f(x)\sin{\lambda x}\mathrm{d}x=0\]
\end{lemma}



Next: A természetes nyelvek kezelése
Up: A matematikai mód
Previous: Elemi függvények Maclaurin sorai
Tartalomjegyzék
Vecsei Balázs
2002-01-15
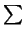
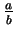
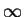
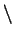 jel vezeti be. A kötelező
paramétereik a {} zárójelpár között vannak, míg az opcionálisokat a
zárójelpár tartalmazza. A {} pár használandó még a blokkok
kijelölésére, a közte lévő karaktereket sok szempontból egy egységként
kezeli a TEX. Egy ilyen pár természetesen tartalmazhat további
parancsokat és {} párokat is.
A TEX-nek alapvetően két üzemmódja van, a szöveges és a
matematikai. A dokumentum matematikát tartalmazó részei vannak a mat
módban. Ebbe kapcsolni a
jel vezeti be. A kötelező
paramétereik a {} zárójelpár között vannak, míg az opcionálisokat a
zárójelpár tartalmazza. A {} pár használandó még a blokkok
kijelölésére, a közte lévő karaktereket sok szempontból egy egységként
kezeli a TEX. Egy ilyen pár természetesen tartalmazhat további
parancsokat és {} párokat is.
A TEX-nek alapvetően két üzemmódja van, a szöveges és a
matematikai. A dokumentum matematikát tartalmazó részei vannak a mat
módban. Ebbe kapcsolni a