A diszkrét macska leképezés.
Adott egy $N \times N$ pixelből álló kép, hajtsuk végre minden $(x,y)$ koordinátájú pontján az alábbi leképezést: \[ T(x,y)=(2x+y, x+y) \quad \mod N \] A leképezést iterálva a kép hamar kaotikussá válik, de tudjuk hogy idővel vissza fogjuk kapni az eredetit. $N$ számelméleti tulajdonságaitól (prímtényezőitől) függ, hogy pontosan hány iteráció múlva történik ez meg, és hogy addig is milyen érdekes jelenségeket figyelhetünk meg.
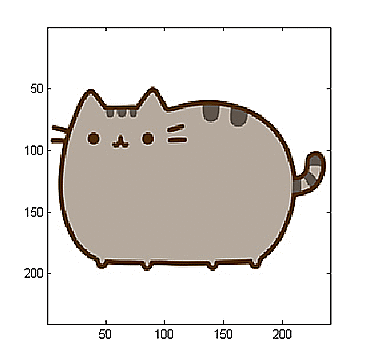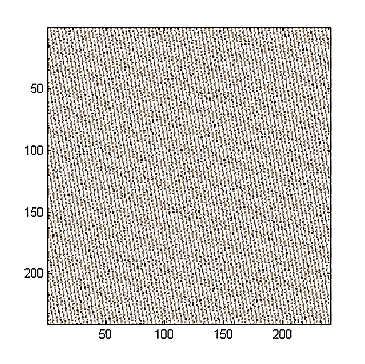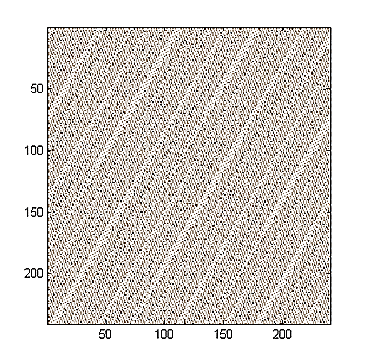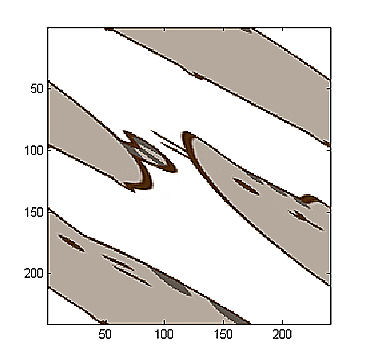
Ez a kép $240 \times 240$ pixeles. Jelöljük $m_N$-el a visszatérési időt. Ekkor az alábbi tétel nyújt segítséget a kiszámolásához:
Tétel. (Forrás: Gregory Gaspari. The Arnold cat map on prime lattices. Physica D: Nonlinear Phenomena, 73(4):352– 372, 1994.) Legyen $N$ prímtényezős felbontása $N=p_1^{\alpha_1}\dots p_k^{\alpha_k}$, ahol $p_j$ prím, és $\alpha_j \in \mathbb{N}$ minden $j=1,\dots,k$ esetében. Ekkor \[ m_N=\text{LKKT}\{ m_{p_1^{\alpha_1}},\dots,m_{p_k^{\alpha_k}} \}, \] ahol LKKT a legkisebb közös többszöröst jelenti.
Mivel $240=2^4 \cdot 3 \cdot 5$, ezért $m_{240}=m_{16} \cdot m_3 \cdot m_5$. Gaspari cikkének a függelékéből kiolvashatjuk, hogy $m_3=4$ és $m_5=10$. Számítógépes kísérletezés segítségével pedig láthatjuk, hogy $m_{16}=12$. (Itt megjegyzem, hogy a kísérletezés során úgy láttam, hogy $m_{2^n}=2^{n-2}m_2=2^{n-2} \cdot 3$, de ennek sehol sem találtam bizonyítását.) Így $m_N=60$.
A $12.$, $24.$, $36.$ és $48.$ iterációban megjelenik az eredeti kép 5 halvány, eltolt példányban (ezeket szellemképeknek szokás nevezni). Ennek az a magyarázata, hogy a leképezés $12.$, $24.$, $36.$ és $48.$ iteráltja úgy tol el minden egyes pontot, hogy egy adott $(x,y)$ koordinátájú pontra az eltolás mértéke attól függ, hogy $y-2x$ milyen maradékot hagy az 5-el való osztás után.
További eredmények a visszatérési időről, a szellemképek magyarázata és egyén érdekességek ebben az írásomban találhatók.
A Matlab kódok, amelyek segítségével az animáció készült elérhetők itt.
Attraktorok ábrázolása.
Egy dinamikai rendszer attraktora az a halmaz, amely minden (vonzási tartományában lévő) pont pályáját bevonzza. Ha a dinamikai rendszer egy differenciálegyenlet-rendszerrel van megadva, a rendszer számos véletlen kezdeti feltételre való numerikus megoldása nagyvonalakban ki fogja nekünk rajzolni az attraktort. Természetesen minél hosszabb időintervallumon oldjuk meg a rendszert és minél több kezdeti feltételből, annál pontosabb képet kapunk. A numerikus megoldás a Matlab beépített ODE-megoldóival könnyen számolható, lássunk pár érdekes példát!
Először vegyünk példának olyan háromváltozós dinamikai rendszereket, amelyek az attraktorukra megszorítva érzékenyek a kezdeti feltételekre (azaz 'kaotikusak'), és az attraktoruk 'különös', azaz fraktál-szerkezetű.
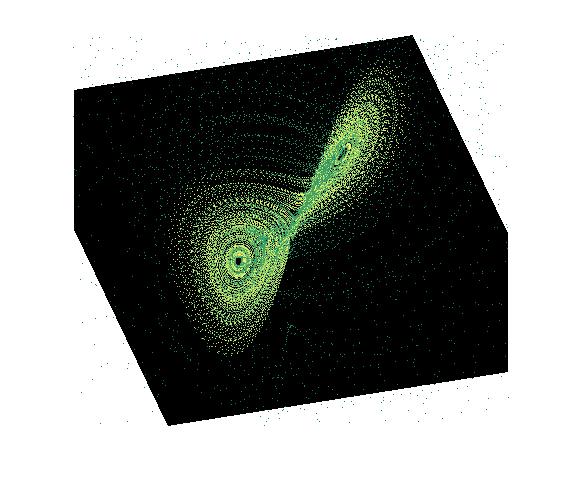
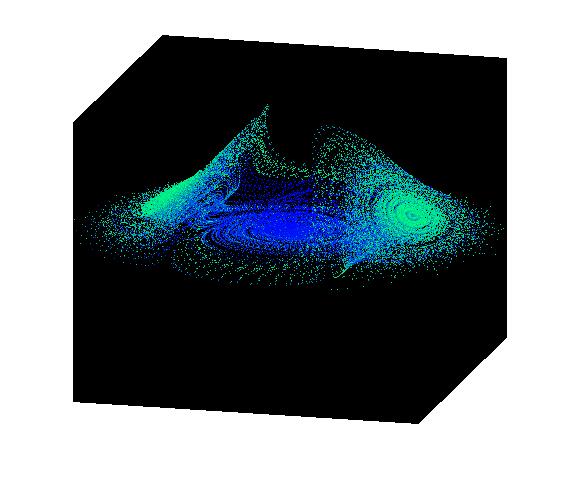
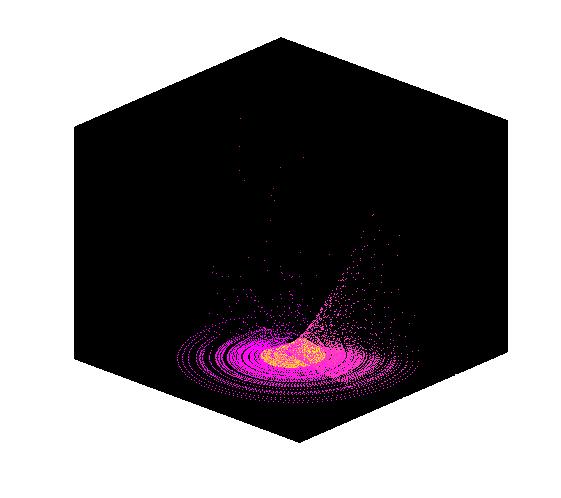
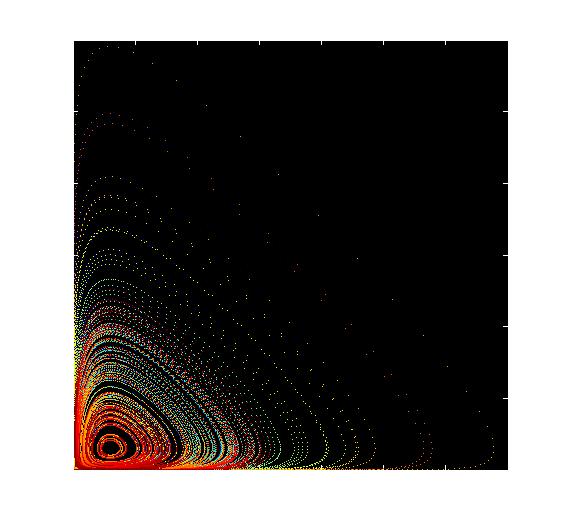
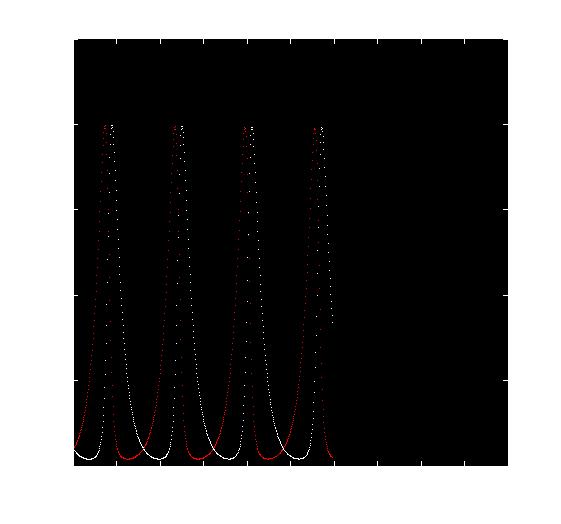
Másfajta érdekes példa a Lotka-Volterra rendszer. Itt a két változó fejlődik, klasszikusan az egyik változó jelképezi egy populációban a ragadozók (rókák) a másik pedig a zsákmányállatok (nyulak) számát. Bármilyen kezdeti állapotból indulva a rendszer egy periodikus pályán marad, azaz a rókák és nyulak száma periodikusan változik az idő múlásával. Lent a baloldali ábrán a róka-nyúl fázissík periodikus pályái rajzolódnak ki, a jobboldali ábrán a fehér görbe a nyulak számának alakulását mutatja, a piros görbe a rókák számának alakulását mutatja, az idő függvényében. (Matlab-kódok)