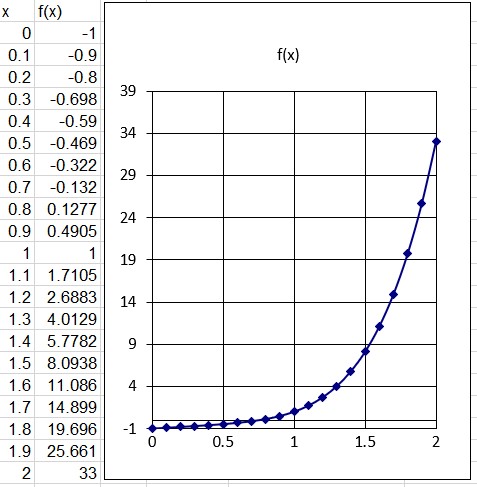
Egy lehetséges megoldás, ha Excelben felsoroljuk tetszőleges bontás szerint a helyeket az x tengely mentén, pl.: 0, 0.1, 0.2, ... 1.9, 2.
Majd mellé lekérjük a polinom értékeit.
Ezután a két oszlopot kijelölve és lekérve az ajánlott diagramok közül a pont diagramot láthatjuk a polinomot a [0,2] intervalllumon.

Pontlevonás jár érte, ha a polinom nem az egész [0,2] intervallumon van felrajzolva. (Vegyétek nyugodtan nagyobbakra a beosztást az y-tengelyen, nem kell 1-esével lépkedni!)
A választott pontok legyenek $a_0=0$ és $b_0=2$.
Győződjünk meg róla, hogy különböző előjelű a függvény értéke az adott pontokban: $f(0)=-1$ és $f(2)=33$, tehát különböző előjelűek.
Ezután a tanult algoritmust (jegyzet 2. oldaltól kezdődően) alkalmazzuk amíg el nem érjük a kellő pontosságot.
A választott példa futtatása itt látható:
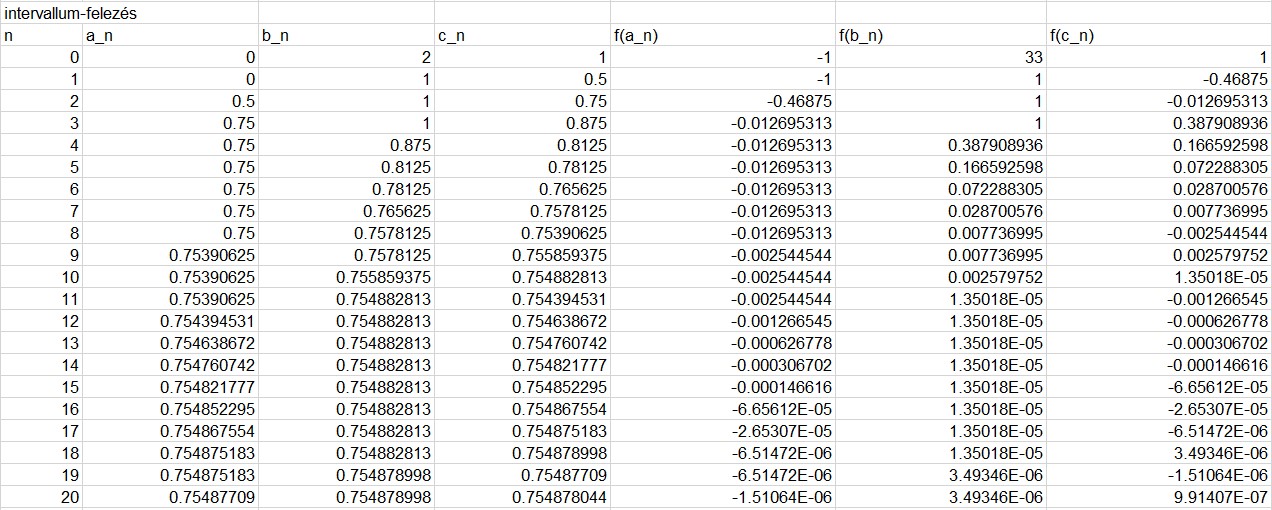
Pontlevonás jár a számolási hibákért, illetve ha nem a megfelelő intervallumokból választjuk a kezdőértékeket! (Elméleti hibáért még nagyobb pontlevonás!)
Legyen a választott pont $x_0=2$.
Alkalmazzuk a tanult algoritmust (jegyzet 5. oldaltól kezdődően) amíg el nem érjük a kellő pontosságot.
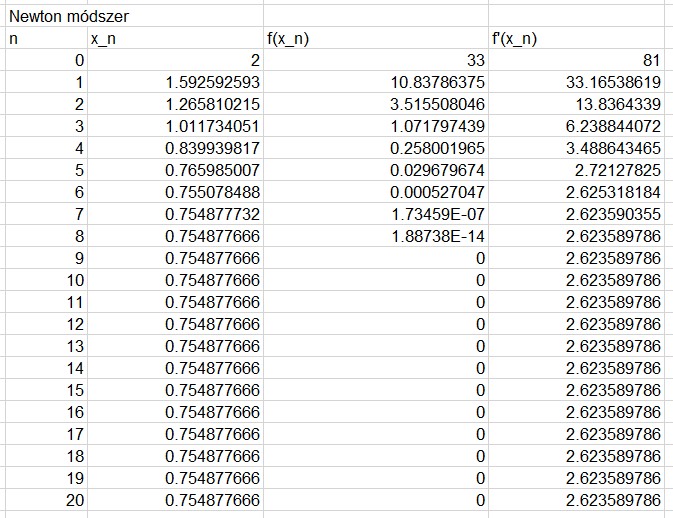
Pontlevonás jár a számolási hibákért (pl.: derivált elszámolása), illetve ha nem a megfelelő intervallumokból választjuk a kezdőértékeket! (Elméleti hibáért még nagyobb pontlevonás!)
Legyen a két választott pont $x_0=2$ és $x_1=\frac{3}{2}$.
Alkalmazzuk a tanult algoritmust (jegyzet 10. oldaltól kezdődően) amíg el nem érjük a kellő pontosságot.

Pontlevonás jár a számolási hibákért (pl.: derivált elszámolása), illetve ha nem a megfelelő intervallumokból választjuk a kezdőértékeket! (Elméleti hibáért még nagyobb pontlevonás!)
A megoldáshoz szükséges elméleti anyag megtalálható a jegyzetben!
A feltételek, melyeket le kell ellenőriznünk: Legyen folytonos, monoton csökkenő és nem negatív.
Integrálszámítások ellenőrzésére bátran használjuk ezt az oldalt. Mivel az oldal levezeti az integrálokat, így én nem fogom külön levezetni azokat. Természetesen a beadandóban pontlevonás jár, ha nincs leírva a számítás. (Ezek nagyon egyszerű integrálok, mindenkinek ki kell tudnia számolni!)
a, Valóban folytonos, monoton csökkenő és nemnegatív, így használhatjuk rá az integrál-kritériumot! Könnyen kiszámolható, hogy az improprius integrál értéke M-től végtelenig: $\frac{1}{M^2}$, azaz véges, így a sorozat konvergens!
b, Szintén folytonos monoton csökkenő és nemnegatív, így használhatjuk rá az integrál-kritériumot. Azonban ebben az esetben az improprius integrál végtelen lesz, mivel a határozatlan integrál $\sqrt{n}+C$, ami a végtelenbe tartva végtelenhez tart, de tetszőleges M helyen véges, így az improprius integrál nem véges, azaz nem konvergens a sorozat!
c, A függvény nem monoton csökkenő! Rajzoltassuk ki a függvényt! Így az integrál-kritérium nem alkalmazható rá!
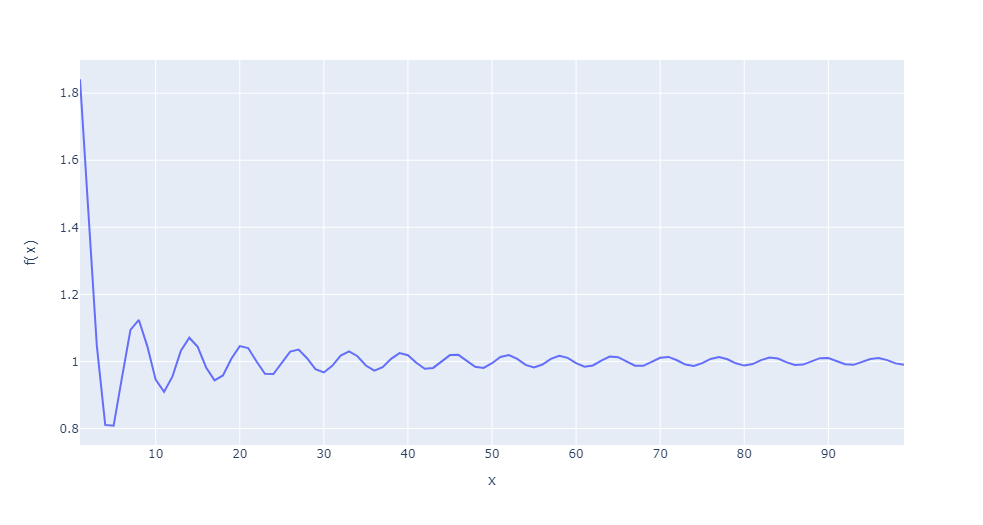
d, A függvény negatív értéket is felvesz, így a kritérium nem alkalmazható rá.
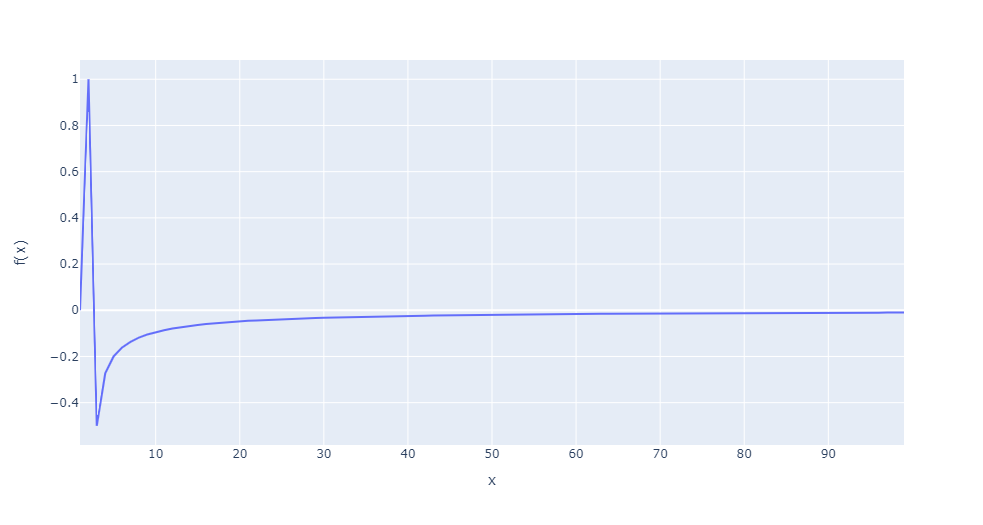
Az a, és b, feladatok 3-3 pontot, míg a c, és d, feladatok 2-2 pontot érnek! INDOKOLNI KÖTELEZŐ! (Az is jó, ha lerajzoljátok a függvényt, de persze elegendő számszerűen megindokolni! Én az egyszerűség kedvéért kirajzoltam, hogy lássuk is őket!)
a, Felülről becsülhető a sorozat az $\frac{5}{n^2}$ sorozattal, melynek soráról tudjuk, hogy konvergens, így maga a sorozat is konvergens.
b, Alulról becsülhető a sorozat például $\frac{1}{16n}$ sorozattal, melynek soráról tudjuk, hogy divergens, így maga a sorozat is divergens.
c, Alulról becsülhető a sorozat a konstans $\frac{1}{2}$ sorozattal, melynek sora nyilvánvalóan divergens, így maga a sorozat is divergens.
Természetesen más helyes becslések is elfogadhatóak.
Az én becsléseim levezetése itt látható.

Az a, és b, feladatok 3-3, a c, feladat 4 pontot ér. INDOKOLNI KÖTELEZŐ! (Ha a becslések nincsenek indokolva, azért pontlevonás jár!)
A számítások ellenőrzésére bátran használjuk ezt az oldalt.
a, Ismerjük fel, hogy ez egy mértani sorozat a következő paraméterekkel: $a_0=2,\ q=\frac{-2}{3}$. Így a tanult képlet (jegyzet 11. oldal) alapján kiszámolható az összeg: $\frac{6}{5}$
b, Ismerjük fel, hogy ez az $e^x$ hatványsora (akár gondolhatunk a következő előadásokra is már, Taylor-sor), de a második előadás jegyzetének utolsó oldalán is szerepel. Vegyük észre, hogy a paraméter $c=-1$, így a sorösszeg értéke $\frac{1}{e}$.
c, Ez egy fokkal nehezebb feladat az eddigieknél, mivel nem tanultunk rá tételt, amivel egyszerűen megoldható lenne. Egy egyszerű levezetést teljes indukcióval itt láthattok.

Az a, és b, feladatok 3-3, a c, feladat 4 pontot ér. INDOKOLNI KÖTELEZŐ! (A korrekt levezetést és indoklást elvárjuk. Az a, és b, feladat esetén hivatkozzunk a tanult anyagra, a c, feladattal egy kicsit elnézőbbek vagyunk, de ott is szükséges indokolni!)
A megoldások ellenőrzéséhez használhatjuk a Symbolab Taylor-sor számolóját. Deriválással együtt szépen levezeti a megoldásokat.
3.1
a & b, Számoljuk ki a függvény deriváltjait!
$f(x)=x^5+2x^3-x-4$
$f'(x)=5x^4+6x^2-1$
$f''(x)=20x^3+12x$
$f'''(x)=60x^2+12$
$f^{(4)}(x)=120x$
$f^{(5)}(x)=120$
$f^{(k)}(x)=0$ ha $k\geq 6$
Helyettesítsünk be a jegyzetben található Taylor-sor képletbe.
A behelyettesítés után a megoldások a, esetben maga $f(x)$ b esetben pedig $-2+10\left(x-1\right)+16\left(x-1\right)^2+12\left(x-1\right)^3+5\left(x-1\right)^4+(x-1)^5$
c, A tipp alapján sejthető, hogy ezt az $e^x$ hatványsorával kell megoldani, valóban: $\sum _{n=0}^{\infty \:}\frac{x^n}{n!}$ képletbe írjunk $x$ helyett $-x^2/2$-őt, így a megoldás:
$$\sum _{n=0}^{\infty \:}\frac{(\frac{-1}{2})^n(x)^{2n}}{n!}$$
d, A tipp alapján alakítsuk át a függvényt $$\frac{1}{2-x}=\frac{1}{2}\cdot\frac{1}{1-\frac{x}{2}}$$ ez pedig szintén egy mértani sorösszeg, melynek a kvóciense $\frac{x}{2}$, így a megoldás: $$\sum _{n=0}^{\infty \:}\left(\frac{1}{2}\right)^{n+1}x^n$$
Az a 2 pontot a b 3 pontot a c 2 pontot és a d 3 pontot érő feladat. Amennyiben nincs az általános alak felírva, csak az első néhány tag és +..., akkor 1 pontlevonás jár.
3.2
A $sin(x)$ hatványsora ismert, az $ln(x)$-nek pedig nincs értelmezve a Taylor-sora a 0 körül, így a táblázatnak az utolsó 3 sora nem érdekes, az első 3-mal foglalkozunk.
A kitöltött táblázat érdemi része így néz ki
| f(x) | n fokszám | Tn(x) Taylor polinom | Tn(0.5) közelítés | f(0.5) pontos érték | hiba (itt abszolút értelemben) |
|---|---|---|---|---|---|
| $$sin(x)$$ | 3 | $$x-\frac{1}{3!}x^3$$ | 0.479166666 | 0.479425538 | 0.000258871 |
| $$sin(x)$$ | 5 | $$x-\frac{1}{3!}x^3+\frac{1}{5!}x^5$$ | 0.479427083 | 0.479425538 | 0.000001544 |
| $$sin(x)$$ | 7 | $$x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7$$ | 0.479425533 | 0.479425538 | 0.000000005 |
1 pont, ha felismerjük, hogy az ln(x)-et nem kell vizsgálni, 1-1-1 pont, ha sin(x) Taylor polinomjait rendesen felírjuk. A többi 6 pont, ha feltöltjük a számokkal a cellákat. Apró eltérésekért pontlevonás nem jár, súlyos, nagy eltérésért pontlevonás adható. Nem jár pontlevonás, ha az ln(x) sorokat valaki teljesen üresen hagyja.
3.3
A megoldás megsejthető a lapon látható módon:

Behelyettesítve $x=0.01$ értéket -9.06-ot kapunk.
Elegendő az óra végén tanult módszert (jegyzet alja 0/0 típusú határértékek) alkalmazni. 8 pont jár a határérték megsejtéséért és további 2 a behelyettesítésért. (Ha a már átalakított, Taylor-polinommal közelített függvénybe helyettesítünk be, akkor 1 pont.)
4.1
Legyen
$A=1,\ B=3+2i,\ C=2+3i,\ D=1+2i,\ E=3$
és
$T(z)=2iz$.
Rajzoljuk le az $A - B - C - D - E - B - D - A -E$ és a $ T(A) - T(B) - T(C) - T(D) - T(E) - T(B) - T(D) - T(A) - T(E)$ töröttvonalakat.
Utóbbihoz ki kell számolnunk a függvények értékeit a megadott helyeken.
$T(A) = 2i$
$T(B) = 2i(3+2i) = -4+6i$
$T(C) = 2i(2+3i) = -6+4i$
$T(D) = 2i(1+2i) = -4+2i$
$T(E) = 6i$
Az alábbi ábrán láthatóak a lerajzolt töröttvonalak.
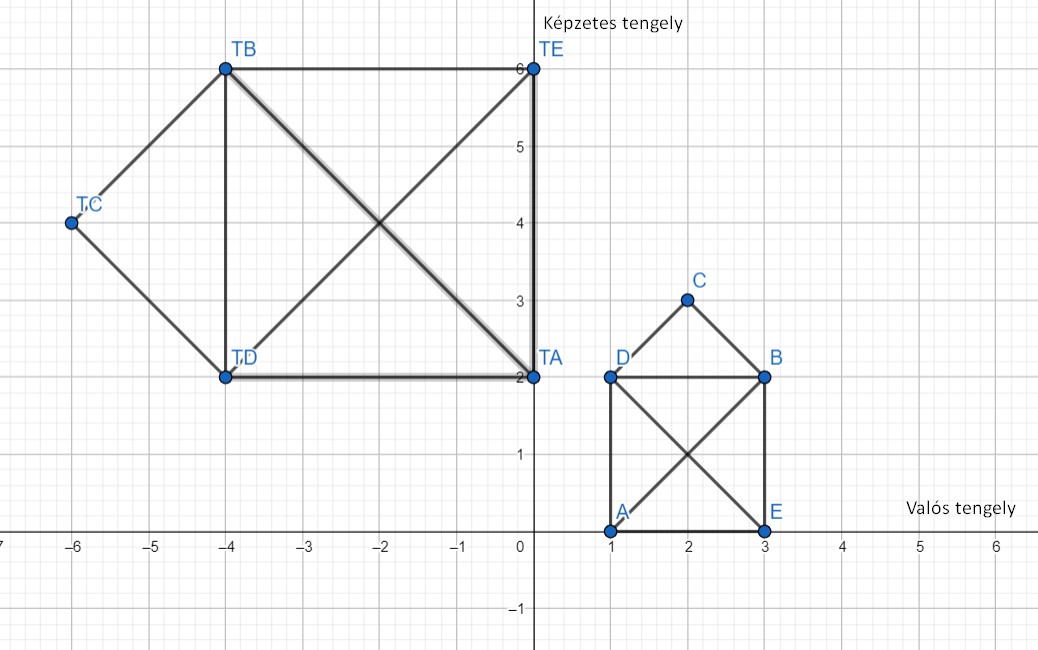
A feladat megoldásához ki kell számolni a megadott pontokban a függvény értékét, majd felrajzolni a töröttvonalakat. Számolási, rajzolási hibák esetén pontlevonás adható.
4.2
a,
Tanultuk (exponenciális alak / Euler-formula alapján), hogy $$\sin(x)=\frac{e^{ix}-e^{-ix}}{2i} \ \ \text{és} \ \ \cos(x)=\frac{e^{ix}+e^{-ix}}{2}.$$
Hasonlóan $$2\sin(x)+3\cos(x)=2\frac{e^{ix}-e^{-ix}}{2i}+3\frac{e^{ix}+e^{-ix}}{2}.$$
Gyűjtsük össze a megfelelő tagok ($e^{ix}$ és $e^{-ix}$) együtthatóit és megkapjuk, hogy $A=\frac{2}{2i}+\frac{3}{2}=\frac{3}{2}-i$, illetve $B=\frac{-2}{2i}+\frac{3}{2}=\frac{3}{2}+i$.
b,
Most ugyanezt a játékot kell eljátszanunk csak visszafele. A fenti alakját a trigonometrikus függvényeknek behelyettesítve azt kapjuk, hogy
$$g(x)=C\frac{e^{ix}+e^{-ix}}{2}+D\frac{e^{ix}-e^{-ix}}{2i}=e^{ix}\left(\frac{C}{2}+\frac{D}{2i}\right)+e^{-ix}\left(\frac{C}{2}-\frac{D}{2i}\right).$$
(Az a,-ban ugyanezt láttuk, csak C=2, D=3.)
A feladat szerint Az első tag együtthatója 2, a második tag együtthatója 3.
Azaz $$\left(\frac{C}{2}+\frac{D}{2i}\right)=2,\left(\frac{C}{2}-\frac{D}{2i}\right)=3,$$
melyet megoldva azt kapjuk, hogy $C=5, D=-i$.
A feladat megoldásánál a trigonometrikus függvények exponenciális alakját kell alkalmazni. Innentől kezdve csak számolás. Számolási hibákra pontlevonás adható. 5-5 pont mindkét feladatrész!
4.3
Itt is használjuk az előbbi alakját a függvényeknek.
$$\cos(x)=\frac{e^{ix}+e^{-ix}}{2}$$
$$2\sin(2x)=2\frac{e^{2ix}-e^{-2ix}}{2i}$$
$$3\cos(3x)=3\frac{e^{3ix}+e^{-3ix}}{2}$$
A függvények ezen alakjából könnyen leolvashatjuk a komplex Fourier sorát.
$a_1=\frac{1}{2}, \ a_{-1}=\frac{1}{2}, \ a_2=-i, \ a_{-2}=i, a_3=\frac{3}{2}, a_{-3}=\frac{3}{2}$
A feladat megoldásánál a trigonometrikus függvények exponenciális alakját kell alkalmazni. Innentől kezdve csak számolás. Számolási hibákra pontlevonás adható.
4.4
Először kezdjük a b, résszel, aztán utána használjuk a szokásos formulát, hogy meghatározzuk az a, részt.
A tanult képlet alapján tudjuk, hogy
$$ f(x)=\frac{A_0}{2}+\sum_{n=1}^{\infty}\bigg[A_n\cos(nx)+B_n\sin(nx)\bigg],$$ ahol az együtthatók
\begin{aligned}A_0&=\frac{1}{\pi}\int_0^{2\pi}f(x)dx\\
&=\frac{1}{\pi}\int_0^{2\pi}xdx\\
&=2\pi,
\end{aligned}
és
\begin{aligned}A_n&=\frac{1}{\pi}\int_0^{2\pi}f(x)\cos(nx)dx\\
&=\frac{1}{\pi}\int_0^{2\pi}x\cos(nx)dx\\
&=0\quad\forall{n}\in\mathbb{N},
\end{aligned}
és
\begin{aligned}B_n&=\frac{1}{\pi}\int_0^{2\pi}f(x)\sin(nx)dx\\
&=\frac{1}{\pi}\int_0^{2\pi}x\sin(nx)dx\\
&=\frac{-2}{n}\quad\forall{n}\in\mathbb{N}.
\end{aligned}
Így $$f(x)=\pi+\sum_{n=1}^{\infty}\frac{-2}{n}\sin(nx).$$
Az integrálok kiszámításához (és egyébként integrálás gyakorlásához) használjuk bátran az integrál kalkulátort, szépen le is vezeti a megoldásokat. Ezek egyszerűen megoldhatóak parciális integrálással. (A koszinusznál pedig sejthetjük, hogy 0 lesz, mivel páratlan függvény szorozva páros függvénnyel az páratlan és páratlan függvény 0 körüli szimmetrikus intervallumon vett integrálja 0.)
Ezt írjuk át komplex alakká az exponenciális alak segítségével.
A feladat megoldásához alkalmazni kell a tanult képleteket. Számolási hibákra pontlevonás adható. 5-5 pont mindkét feladatrész!
5.1
Egy szép ábra, rajta a lokális maximummal (sötét kék, ez egyben globális maximum is), a nyeregponttal (világos kék), és a két globális minimummal (piros). FIGYELEM: Az ábrán nincsenek rajta a határok, ne felejtsük, hogy $-1\leq x \leq 3$ és $-1\leq y \leq 3$ között kell nézni.
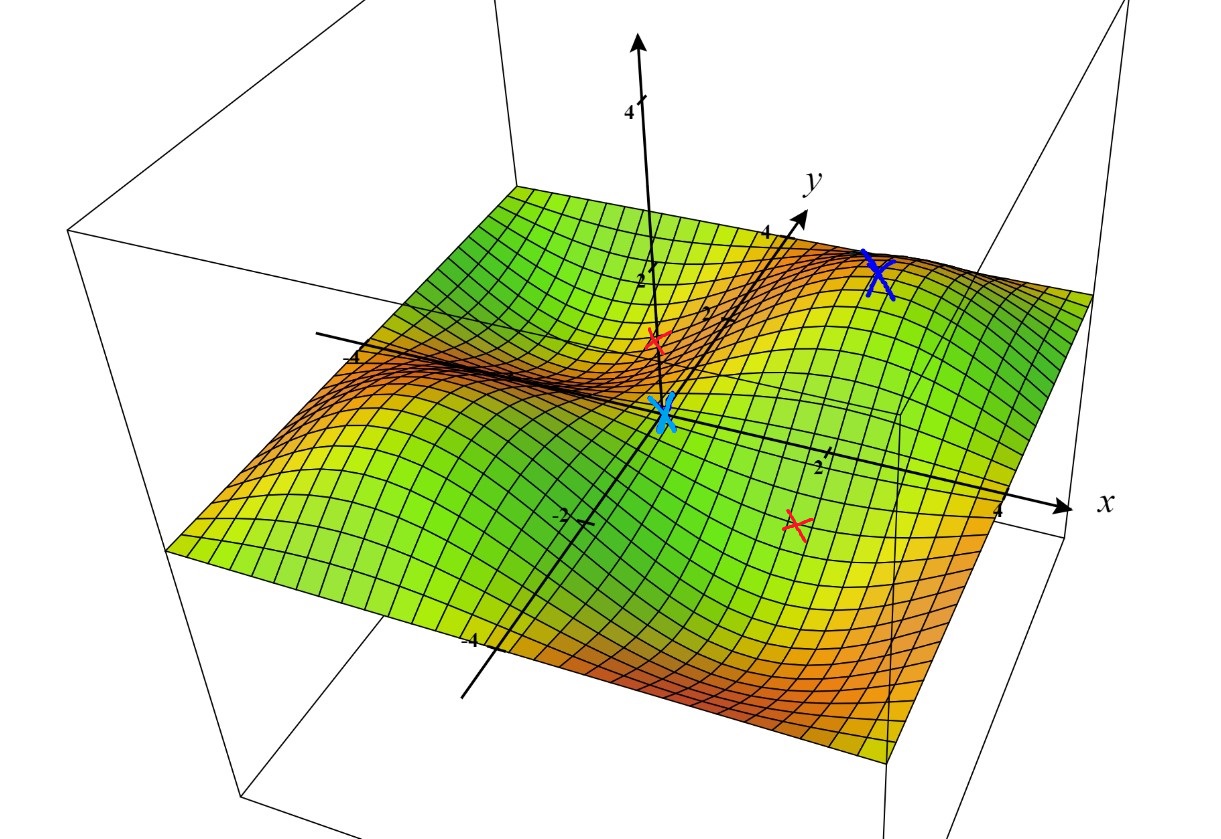
Megoldások. Sajnos nem volt időm begépelni, így papíron lesznek.


5.2
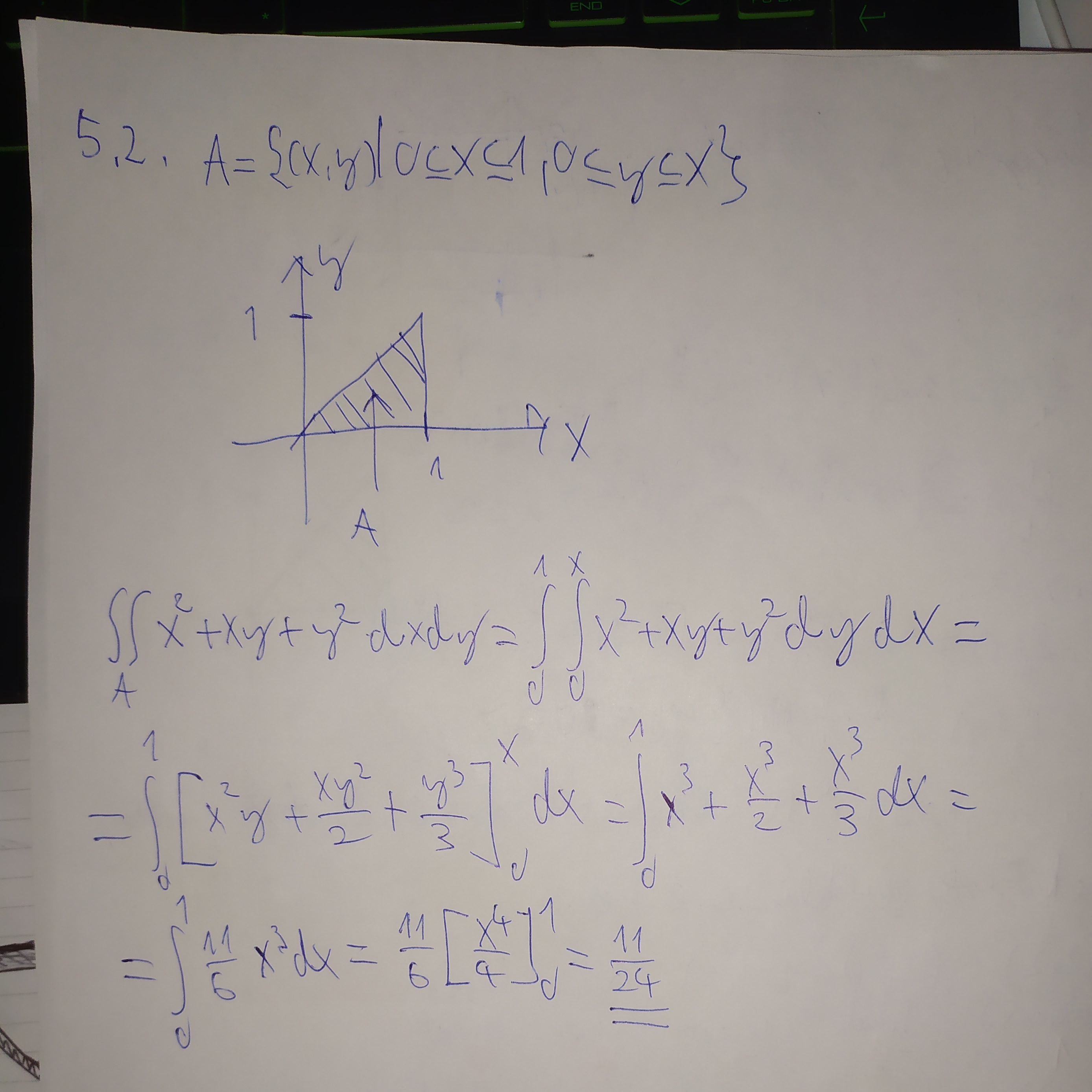
5.3
