A végtelen láncok legegyszerűbben úgy kezelhetőek, hogy a paraméter értékekre
bevezetünk egy felső korlátot, és ha ezt átlépnénk, akkor is visszatérünk. Ezzel
a megoldással sajnos nagyon sok esetet elveszítünk (a végtelen láncokat...) de a
módszer finomítható.
Szeretnénk felismerni a végtelen láncokat és az összes lehetséges véges esetet
is. Ezen célunk eléréséhez sajnos továbbra is szükségünk lesz az előbb említett
felső korlátokra, de a felső korlát ügyes beállításával az összes esetet fel
tudjuk sorolni (sajnos a felső korlát értékét csak tapogatjuk.) A módszer alapja
a következő: előállítjuk a véges eseteket a felső korlátig, első körben a
minimális paraméter értékek helyére minden lehetséges módon megpróbálunk
végtelent helyettesíteni. Második
körben ellenőrizzük, hogy ha bármely másik paramétert végtelennek választjuk,
akkor elromlik a görbület (azaz az éppen vizsgált kombinációt nem tartalmazza
egy másik).
Az előbbi algoritmust úgy módosítjuk, hogy a paraméter értékek kiíratása helyett
alkalmazzuk a következő algoritmust a végtelen láncok felismerésére. Újra a jól
bevált backtrack algoritmust használjuk: (a paraméterlista első elemével
indítva)
Algoritmus 3.7
Az első körben:
- Ha a paraméterlista végén vagyunk, elindítjuk a második kört a
paraméterlista első elemével indulva.
- Különben ha az aktuális paraméter értéke egyenlő a minimális értékével
és végtelennek választva nem romlik el a görbületi kritérium, akkor
behelyettesítünk végtelent (alacsonyabb szintű nyelvben egy elég nagy
számot), és meghívjuk a következő paraméterre az algoritmus első körét.
Miután végzett a rekurzív rész, visszaállítjuk a minimális értéket.
- Végül az előző lépés végre(nem)hajtásától függetlenül lefuttatjuk az
első kört a következő paraméterre is.
Mostanra biztosítottuk, hogy a paraméterlista teljesíti a görbületi
kritériumot úgy, hogy néhány paraméter helyén végtelen is lehet.
Biztosítanunk kell még, hogy egy ilyen paraméterlistának egyik véges elemébe
sem tudunk végtelent helyettesíteni, különben az így kapott többparaméteres
végtelen lánc tartalmazná az előbbit.
A második körben:
- Ha a lista végén vagyunk, írjuk ki az esetleg már végteleneket is
tartalmazó láncot.
- Különben nézzük meg, hogy az aktuális paramétert választhatjuk-e
végtelennek a görbület megsértése nélkül, ha igen, visszatérünk; ha nem,
akkor meghívjuk a második kört a következő paraméterre.
Az algoritmus végére minden olyan végtelen láncot pontosan egyszer írtunk ki,
amit a felső korlát figyelembevételével megtalálhattunk. Ezenkívül minden
végtelen lánc illetve véges eset maximális, azaz nincs olyan több szabad
paraméteres végtelen lánc, aminek részeként megkapnánk.
Fontos még megjegyezni, hogy a felső korlátot hogyan lehet beállítani: először
veszünk neki egy tetszőleges értéket. Ha találunk olyan paraméter értékeket, ahol
legalább az egyik paraméter értéke eléri a felső korlátot, és a helyére nem
tudunk végtelent helyettesíteni, akkor növelni kell a felső korlátot.
Megjegyezzük még, hogy a legfeljebb 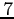 elemű D-szimbólumok körében ez a felső
korlát
elemű D-szimbólumok körében ez a felső
korlát 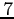 . Azaz ha egy paraméter elérte a
. Azaz ha egy paraméter elérte a 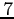 -es értéket, akkor ott már
végtelen láncot találtunk. Ezt az eredményt a mellékelt program adta, egyelőre
az elméleti alapokat csak találgatjuk.
-es értéket, akkor ott már
végtelen láncot találtunk. Ezt az eredményt a mellékelt program adta, egyelőre
az elméleti alapokat csak találgatjuk.
Boroczki Lajos
2007-05-29
![]() elemű D-szimbólumok körében ez a felső
korlát
elemű D-szimbólumok körében ez a felső
korlát ![]() . Azaz ha egy paraméter elérte a
. Azaz ha egy paraméter elérte a ![]() -es értéket, akkor ott már
végtelen láncot találtunk. Ezt az eredményt a mellékelt program adta, egyelőre
az elméleti alapokat csak találgatjuk.
-es értéket, akkor ott már
végtelen láncot találtunk. Ezt az eredményt a mellékelt program adta, egyelőre
az elméleti alapokat csak találgatjuk.