Átsorszámozhatóság

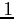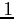Újra elővesszük a szimmetrikus diagramokat: Ha találunk olyan nem $1$ csúcsot a diagramban, amiből indítva a sorszámozást ugyanolyan diagramot kapunk, mint az $1$ -ből indított számozáskor; akkor párhuzamosan elkezdjük vizsgálni a mátrix-függvények értékeit és az első különböző értéknél megállunk. Ha az eredeti sorszámozás szerinti érték kisebb, akkor nem sorszámozható át, ha az új sorszámozás szerinti kisebb, akkor átsorszámozható a D-szimbólum, ezért eldobhatjuk (mert a kisebb is előáll.)

Algoritmus 3.8   Minden 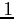$1$ -től különböző sorszámozás esetén megnézzük a következőket:

• Ha a diagramok különbözőek (azaz a nem 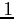$1$ -gyel kezdődő sorszámozás nagyobb, akkor ezzel a sorszámozással nem foglalkozunk.)
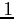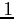• Különben lexikografikusan haladunk végig a szomszédos operációkon: első a kisebbik sorszámú operáció sorszáma, második az aktuális szimplex (illetve diagram-csúcs) sorszáma. Az első különböző esetén vége az algoritmusnak, ha nem az $1$ szerinti sorszámozásnál kisebb a mátrix értéke. Ha az $1$ szerinti sorszámozásnál kisebb, akkor vesszük a következő lehetséges sorszámozást.

Ha sehol sem léptünk ki, akkor megtartjuk a paraméterlistát, mert nem lehet átsorszámozni a mátrix-függvény figyelembevételével sem.

Ezen a ponton újra előkerül a probléma, hogy a végtelen láncokat hogyan is kezeljük, ugyanis a következő rész miatt nem választhatunk azonos nagy számot végtelennek (illetve nem válaszolhatjuk azt, hogy igen, a végtelen egyenlő-e végtelennel kérdésre, mert az átsorszámozás esetén az igen válasz célszerű, míg a következő részben bővebben kifejtett maximalitás esetén pont az ellenkezője.) A problémát a következőképpen orvosolhatjuk: mindig ha egy paraméter értékének nagy számot választunk (mivel végtelent nem tudunk), akkor a nagy szám értékét növeljük 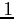$1$ -gyel. Ezzel, és a fenti paraméter változtatgató algoritmusokkal biztosítjuk, hogy a végtelen paraméterek növekvő sorrendben legyenek. Így a mátrix-függvényekben is igaz, hogy a végtelen paraméterek első megjelenései növekvő sorrendben vannak (a mátrix-függvények szabad paramétereinek a fent említett lexikografikus rendezése esetén.)