A realizáció kérdése példákon

Most nézzünk két példát a realizációra is. Az első példa a 47-es sorszámú, 3 dimenziós 6 elemű D-szimbólum. D-diagramja fig:d3c647d. ábrán látható. Az $\mathcal{R}$ mátrix-függvénye a következő:

$$i\in\{1,2,3,6\}: \mathcal{R}(D_i)= \left( \begin{array}{cccc} 1 & 4 & 2 & 2 \\ 4 & 1 & 3 & 2 \\ 2 & 3 & 1 & 2 \\ 2 & 2 & 2 & 1 \end{array}\right)$$

$$i\in\{4,5\}: \mathcal{R}(D_i)= \left( \begin{array}{cccc} 1 & 2 & 2 & 2 \\ 2 & 1 & 3 & 2 \\ 2 & 3 & 1 & 2 \\ 2 & 2 & 2 & 1 \end{array}\right)$$

Figure: A 47-es sorszámú 3 dimenziós 6 elemű diagram

Figure: A 47-es sorszámú D-szimbólum elemzése

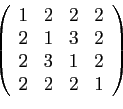A D-szimbólum a következő kisebb dimenziós komponensekre esik szét fig:47adatok. ábra alapján:

• A csúcs szerinti $\sigma_0$ szomszédságot elhagyva nem esik szét,
• az él szerintit ($\sigma_1$ -et) elhagyva 3 részre,
• a lapközéppont szerintit ($\sigma_2$ -t) elhagyva 2 részre,
• végül a testközéppont szerintit ($\sigma_3$ -at) elhagyva sem esik szét.

A következő információkat is leolvashatjuk az előbbi 7. ábráról:

• Duálisa a 95-ös sorszámú szimbólum.
• A paramétereket együtthatóikkal és hogy a hozzájuk tartozó pályákon van-e síktükrözés (ha nem szerepel $+$ , akkor van.)
• Az $\mathcal{M}$ mátrix-függvényt paraméteresen (balról jobbra, majd fentről lefelé olvasva.)
• Végül a paraméterek lehetséges értékeit az adott érték esetén előforduló végtelen távoli (ideális) csúcs létével és a maximalitással együtt. (Illetve hogy a csúcs és testközéppont szerinti operáció elhagyása esetén létrejöhet-e rossz orbifold.)

Látható, hogy $m=1, n=2, o=3, p=q=r=2$ esetén visszakapjuk a kocka kövezést (ugyanis minden mátrix egyenlő lesz). Viszont a $q\not=r$ esetben már maximális a D-szimbólum. A kövezés alappoliédere $m=1, n=2, o=3$ esetén egy olyan poliéder, aminek két szemközti lapja egybevágó, de egymáshoz képest elforgatott téglalap, a palástja pedig egybevágó szimmetrikus trapézokból áll. A pontos felépítés és a baricentrikus felbontás fig:d3c647f. és fig:d3c647b ábrákon látható.

Figure: A 47-es sorszámú kövezés fundamentális tartománya

Figure: A 47-es sorszámú kövezés teljes baricentrikus felbontása

Ha $q$ vagy $r$ értékét növeljük, akkor a téglalapok rövidebb illetve hosszabb oldala körüli poliéderek számát változtatjuk. Ha mindkettő $2$ , akkor Euklideszi térben valósul meg (kockarács), ha legalább az egyikük nagyobb, akkor valószínűleg hiperbolikus $H^3$ geometriában realizálhatóak.

Másik példaként vizsgáljuk meg részletesebben sec:pelda1 részben leírt kövezést. Vizsgáljuk meg újra fig:kocka2d. ábra diagramját. Látható, hogy ha az él- és lapközéppontok szerinti rossz orbifoldokat kiszűrjük, vagyis egyenlőnek választjuk a megfelelő paramétereket, akkor a következő paraméteres $\mathcal{M}$ mátrix-függvényt kapjuk:

$$\mathcal{M}(D_1)= \left( \begin{array}{cccc} 1 & 2m & 2 & 2 \... ...o & 2 \\ 2 & 3o & 1 & 4q \\ 2 & 2 & 4q & 1 \end{array}\right) \mathcal{M}(D_2)= \left( \begin{array}{cccc} 1 & 2m & 2 & 2 \... ...p & 2 \\ 2 & 3p & 1 & 4q \\ 2 & 2 & 4q & 1 \end{array}\right)$$

$$\mathcal{M}(D_3)= \left( \begin{array}{cccc} 1 & 4n & 2 & 2 \... ...p & 2 \\ 2 & 3p & 1 & 4q \\ 2 & 2 & 4q & 1 \end{array}\right) \mathcal{M}(D_4)= \left( \begin{array}{cccc} 1 & 4n & 2 & 2 \... ...o & 2 \\ 2 & 3o & 1 & 4q \\ 2 & 2 & 4q & 1 \end{array}\right)$$

$$\mathcal{M}(D_5)= \left( \begin{array}{cccc} 1 & 4n & 2 & 2 \... ...o & 2 \\ 2 & 3o & 1 & 2r \\ 2 & 2 & 2r & 1 \end{array}\right) \mathcal{M}(D_6)= \left( \begin{array}{cccc} 1 & 4n & 2 & 2 \... ...p & 2 \\ 2 & 3p & 1 & 2r \\ 2 & 2 & 2r & 1 \end{array}\right)$$

Programunk két lényegesen különböző lehetséges paraméterláncot talált:

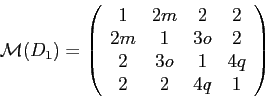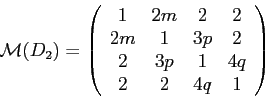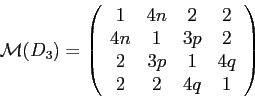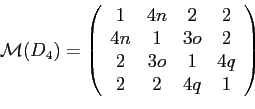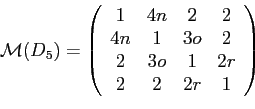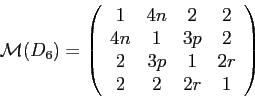m	n	o	p	q	r
m>2	1	1	1	1	r>2
m>2	1	1	1	2	2

Mindkét lánc esetén igaz, hogy nem maximálisak, ugyanis az 1-es és 2-es, 3-as és 4-es illetve 5-ös és 6-os csúcsok összevonhatóak, és így kapunk egy 3 elemű szimbólumot. Az első láncban $m=r=2$ -t választva visszakapjuk a kockakövezés szimmetriatörését, így ez euklideszi térben megvalósuló kövezést ad. Az első lánc összes többi esetében igaz, hogy a két él (baricentrikus-szimplex él) - amelyek körüli poliéderek számát az $m$ és az $r$ meghatározza - párhuzamos egymással, így a körülöttük levő poliéderek számának növelése egyértelműen leírható a rájuk merőleges síkban is. Ez a sík hiperbolikus, ha $m$ és $r$ közül legalább az egyik nagyobb, mint $2$ . Tehát az első végtelen lánc a legelső eset kivételével $H^2\times R$ tér kövezéséhez vezet.

A második paraméterlánc esetén a kövezés poliédereinek minden csúcsa végtelen távoli pont (mert csak 1 csúcsosztály van és van ideális csúcs), így valószínűsíthetjük, hogy hiperbolikus $H^3$ térben valósul meg.