A következő problémára keressük a választ ([13,17,14] cikkek alapján):
Adott
 D-szimbólumra
állítsunk elő egy egyszeresen összefüggő d-dimenziós
teret
D-szimbólumra
állítsunk elő egy egyszeresen összefüggő d-dimenziós
teret
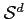 -t, illetve rajta egy
-t, illetve rajta egy
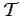 kövezést, aminek
baricentrikus felbontása
kövezést, aminek
baricentrikus felbontása
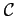 .
.
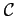 csúcs-osztályait
csúcs-osztályait 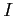 -vel
jelöljük.
-vel
jelöljük. 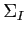 szomszádsági operációk
szomszádsági operációk
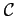 -n való bal-hatása
kompatibilis kell legyen egy
-n való bal-hatása
kompatibilis kell legyen egy
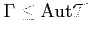 csoporttal, ami
a kövezés szimmetria-csoportja lesz. Megköveteljük, hogy a szimplex-pályákra
alkalmazott szomszédsági operációk rendszere izomorf legyen a D-szimbólummal.
Végül az
csoporttal, ami
a kövezés szimmetria-csoportja lesz. Megköveteljük, hogy a szimplex-pályákra
alkalmazott szomszédsági operációk rendszere izomorf legyen a D-szimbólummal.
Végül az
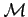 mátrix-függvény megegyezzen a baricentrikus felbontás
megfelelő élei körüli szimplexek számának felével. Ha létezik ilyen, azt a
mátrix-függvény megegyezzen a baricentrikus felbontás
megfelelő élei körüli szimplexek számának felével. Ha létezik ilyen, azt a
 D-szimbólum topologikus (orbifold) realizációjának
nevezzük. Általánosan nehéz eldönteni, hogy van-e ilyen és hogy a 8 lehetséges
homogén geometria közül melyikben valósulhat meg.
D-szimbólum topologikus (orbifold) realizációjának
nevezzük. Általánosan nehéz eldönteni, hogy van-e ilyen és hogy a 8 lehetséges
homogén geometria közül melyikben valósulhat meg.
Subsections
Boroczki Lajos
2007-05-29