For IID bits, see the question and the results in Part I, a few papers below. In this sequel, we consider spin systems that are relatives of IID measures in one way or another, with our main focus being on the Ising model on finite transitive graphs or exhaustions of lattices. We prove that no sparse reconstruction is possible for the entire high temperature regime on Euclidean boxes and the Curie-Weiss model, while sparse reconstruction for the majority function of the spins is possible in the critical and low temperature regimes. We give quantitative bounds for two-dimensional boxes and the Curie-Weiss model, sharp in the latter case.
The proofs employ several different methods, including factor of IID and FK random cluster representations, strong spatial mixing, a generalization of discrete Fourier analysis to Divide-and-Color models, and entropy inequalities. Our results and methods are intended to serve as some baby versions of noise sensitivity results beyond IID bits.
Structural results for the Tree Builder Random Walk. [arXiv:2311.187342 math.PR] With János Engländer, Giulio Iacobelli, and Rodrigo Ribeiro. 34 pages, to appear in Ann. Appl. Prob.
How does the Barabási-Albert type Preferential Attachment growth arise in actual networks, what is the exact mechanism that tells us that already rich vertices must get richer faster? In a social or economic network, such mechanisms are very easy to imagine, but in more physical settings one would like to see some completely local mechanism, not a global distribution of wealth. The Tree Builder Random Walk is a randomly growing tree model achieving this.
This is a random tree built by a walker as she is walking around the tree. At each time n, she adds a leaf to her current vertex with probability n^{-\gamma}, where \gamma \in (2/3, 1], then moves to a uniform random neighbor on the possibly modified tree. We show that the tree process at its growth times, after a random finite number of steps, can be coupled to be identical to the Barabási-Albert preferential attachment tree model. This coupling implies that many properties known for the BA-model, such as diameter and degree distribution, can be directly transferred to our model.
The \gamma=0 case and its variations are well-understood, the tree is growing linearly. For \gamma \in (0, 1/2), the random walker should be transient, but this has not been proved. And how does the tree look like? We don't even have a conjecture for what happens at \gamma=1/2. And how does the tree look like for \gamma \in (1/2,2/3]?
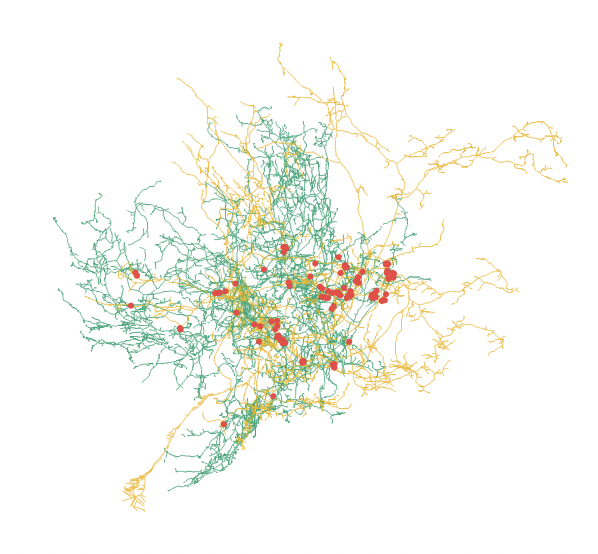
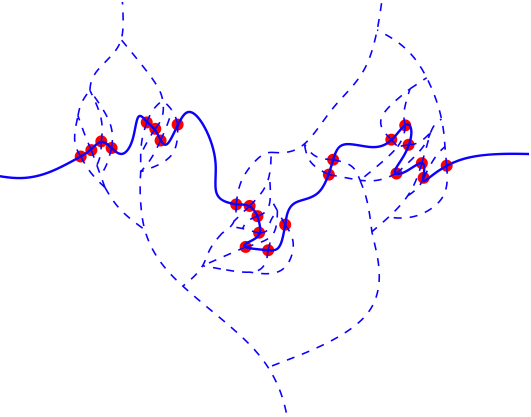
Physical networks as network-of-networks. [arXiv:2306.01583 cond-mat.stat-mech] With Ádám Timár, Sigurdur Örn Stefánsson, Ivan Bonamassa, and Márton Pósfai. Nature Communications 15 (2024), article number 4882. Paper in the journal.
Physical networks are made of nodes and links that are physical objects embedded in a geometric space. Understanding how the mutual volume exclusion between these elements affects the structure and function of physical networks calls for a suitable generalization of network theory. Here, we introduce a network-of-networks framework where we describe the shape of each extended physical node as a network embedded in space and these networks are bound together by physical links. (Think of neurons that look like random graphs themselves, embedded disjointly into space, connected to each other by one or more spatially pretty localized edges, the synapses. In the rightmost picture, two neurons in a fruit fly brain are shown, with red dots at the connecting synapses.)
Relying on this representation, we model the growth of physical networks, showing for a general class of systems that volume exclusion induces heterogeneity (a.k.a. polynomial tails or scale invariance) in both node volume and degree, with the two becoming correlated. A special case is where the extended physical nodes are Loop-Erased Random Walk trajectories, giving rise to a fragmented UST model via Wilson's algorithm.
These emergent structural properties strongly affect the dynamics on physical networks: by calculating their Laplacian spectrum as a function of the coupling strength between the nodes we show that volume-degree correlations suppress the tail of the spectrum. Finally, we apply our theoretical framework to a large-scale three-dimensional map of a fruit fly brain, finding analogous behavior with the networks generated by our growth model.
This is a physics paper. One or more math papers on the fragmented UST model in dim=2 and dim\ge 5 and on the complete graph will follow.
Stake-governed tug-of-war and the biased infinity Laplacian. [arXiv:2206.08300 math.PR] With Yujie Fu and Alan Hammond. Preprint, 71 pages.
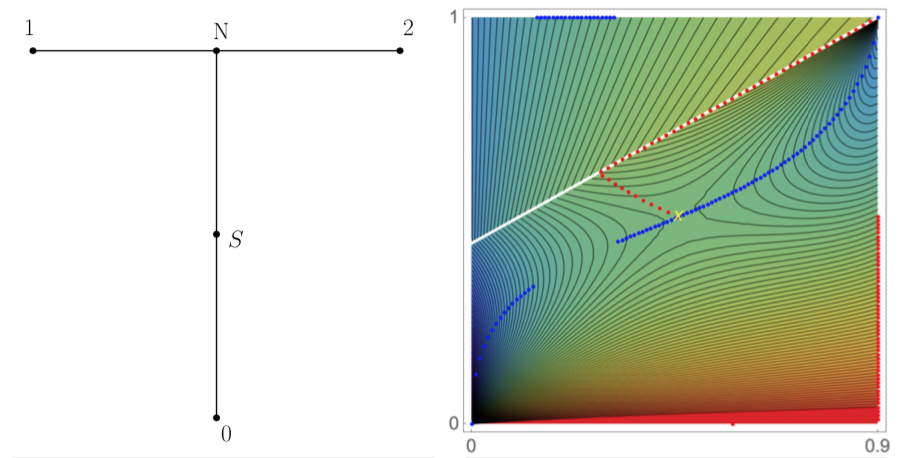
We introduce a version of the Peres-Schramm-Sheffield-Wilson (2009) probabilistic game of random tug-of-war on graphs. Each player has a certain fortune, and there is a token at one of the vertices of a finite graph. Before each move, the players stake some portion of their fortunes, then a coin is tossed, weighted in proportion to the players' stakes, and the winner gets to move the token to a neighbouring vertex on the graph. An extra "regularizing" tweak is that the game is leisurely: the move actually takes place only with a fixed epsilon probability. The game is over when the token reaches a "boundary" vertex, with a fixed amount paid by player Mina to player Maxine. So, obviously, Mina wants to end up at a boundary vertex where the payoff is low, while Maxine, where the payoff is high. Any fortune left with the players at the end of the game is considered negligible compared to the payoff.
So, this game is a metaphor for how to optimally convert economic position into positional advantage.
We determine the Nash equilibria for the game when the graph is a finite tree, with a single leaf having payoff value 1, some other leafs having payoff value 0, and epsilon is small enough. The picture on the right depicts the expected payoff and the opponent's best response, when the game on this graph is started from the vertex N with fortune 0.9 for Maxine and 1 for Mina, as a function of the players' stake in the first round.
It turns out that our game has been studied under the name "Colonel Blotto games" in the economics literature for decades, and we are solving the game in a much greater generality than what was hoped, with the leisurely regularization that looks more natural than regularizations considered earlier.
Finite-energy infinite clusters without anchored expansion. [arXiv:2011.01377 math.PR] With Ádám Timár. Bernoulli 27 (2021), 2353-2361. Paper in the journal.
Hermon and Hutchcroft have recently proved the long-standing conjecture that in Bernoulli(p) bond percolation on any nonamenable transitive graph G, at any p > p_c(G), the probability that the cluster of the origin is finite but has a large volume n decays exponentially in n. A corollary is that all infinite clusters have anchored expansion almost surely. They have asked if these results could hold more generally, for any finite energy ergodic invariant percolation. We give a counterexample, an invariant percolation on the 4-regular tree.
Given a Boolean function of a large number of iid random input bits, we say that there is sparse reconstruction if there is a small subset of the coordinates such that knowing the input there gives us a non-vanishing amount of information about the output.
We show no sparse reconstruction is possible for any transitive function. We discuss the question in different frameworks, measuring information content in L^2 and with entropy. We also highlight some interesting connections with cooperative game theory. Beyond transitive functions, we show that the left-right crossing event for critical planar percolation on the square lattice does not admit sparse reconstruction either. Some of these results answer questions posed by Itai Benjamini.
The Free Uniform Spanning Forest is disconnected in some virtually free groups, depending on the generator set. [arXiv:2006.06387 math.PR] With Ádám Timár. Ann. Probab. 50 (2022) 2218-2243. Paper in the journal.
We prove the rather counterintuitive result that there exist finite transitive graphs H and integers k such that the Free Uniform Spanning Forest in the direct product of the k-regular tree and H has infinitely many trees almost surely.
This shows that the number of trees in the FUSF is not a quasi-isometry invariant. Moreover, we give two different Cayley graphs of the same virtually free group such that the FUSF has infinitely many trees in one, but is connected in the other, answering a question of Lyons and Peres (2016) in the negative.
A version of our argument gives an example of a non-unimodular transitive graph where WUSF\not=FUSF, but some of the FUSF trees are light with respect to Haar measure. This disproves a conjecture of Tang (2019).
There are 13 open problems at the end of the paper. Check them out! It might be that our examples will put an end to Damien Gaboriau's suggestion that the first \ell^2-Betti number versus measurable cost question can be solved via the FUSF.
We find the total variation mixing time of the interchange process on the dumbbell graph (two complete graphs, K_n and K_m, connected by a single edge), and show that this sequence of chains exhibits the cutoff phenomenon precisely when the smaller size m goes to infinity. The mixing time undergoes a phase transition at m\asymp\sqrt{n}. We also state a conjecture on when exactly cutoff holds for the interchange process on general graphs: when the mixing is not governed by a local obstacle.
Our proofs use coupling methods, and they also give the mixing time of the simple exclusion process of k labelled particles in the complete graph K_n, for any k\leq n, with cutoff, as conjectured by Lacoin and Leblond (2011). In particular, this is a new probabilistic proof for the mixing time of random transpositions, first established by Diaconis and Shahshahani (1981).
Kazhdan groups have cost 1. [arXiv:1810.11015 math.GR] With Tom Hutchcroft. Inventiones Mathematicae 221 (2020), 873-891. Paper in the journal.
We prove that every countably infinite group with Kazhdan's property (T) has cost 1, answering a well-known question of Gaboriau. It remains open if they have fixed price 1.
Also, our construction seems to behave very differently on Z^2 and Z^3, which is quite interesting. On these pictures, we see that the iterations of our subcritical Z^2 construction seem to have more and more critical-like clusters.
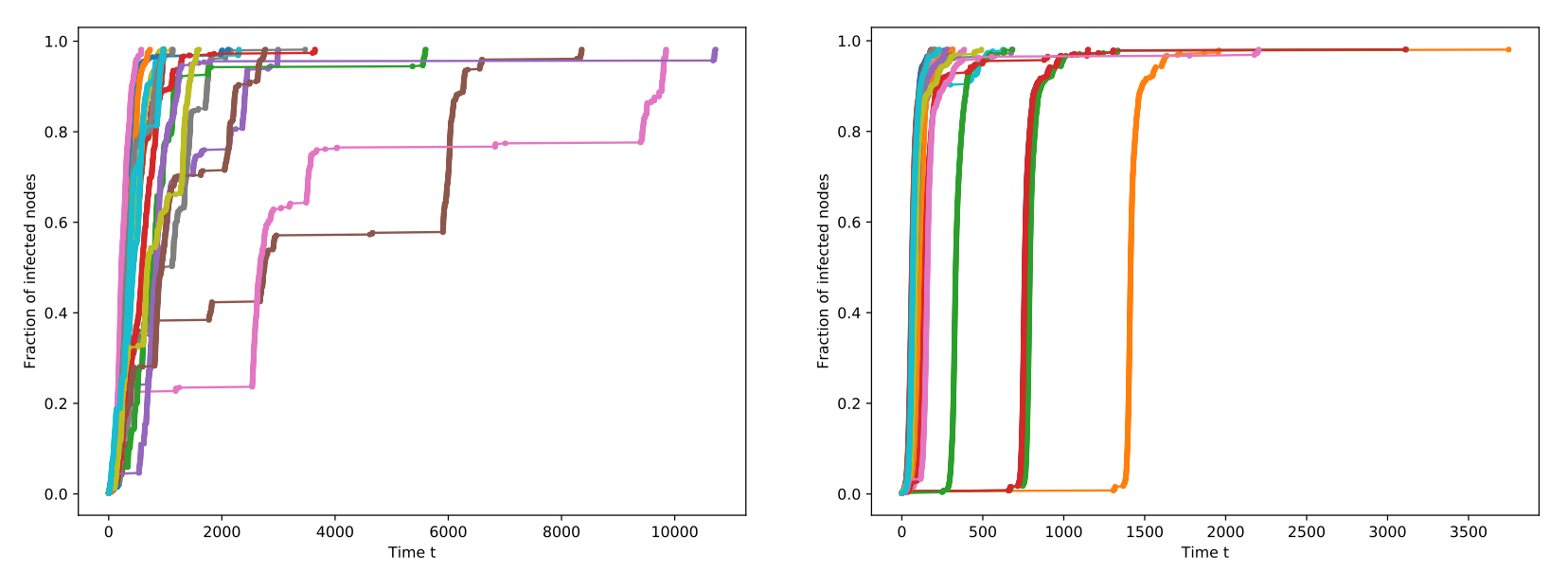Speeding up non-Markovian First Passage Percolation with a few extra edges. [arXiv:1708.09652 math.PR] With Alexey Medvedev. Adv. Appl. Probab. 50 (2018), 858-886. Paper in the journal.
Consider FPP with heavy-tailed edges-weights P[X>t]=t^{-\alpha}, \alpha<1, on the largest cluster of a near-critical Erdos-Renyi graph G(n,1/n+\lambda n^{-4/3}). For \lambda=0, the spreading is typically slow, with huge plateaux. For \lambda >>1, most of the spreading is fast and smooth. That is, just a few extra edges radically speed up and smooth out the process. In the paper, we understand which proportion of an arbitrary graph is occupied fast, and study what this proportion is in the case of near-critical Erdos-Renyi graphs and large critical Galton-Watson trees with an extra edge added.
Carmesin, Federici, and Georgakopoulos [arXiv:1603.06712] constructed a transient hyperbolic graph that has no transient subtrees and that has the Liouville property for harmonic functions. Such graphs must be far from transitive. Nevertheless, we modify their construction to get a unimodular random graph with the same properties.
We study the natural generalizations of the usual notions of critical density of Bernoulli percolation from transitive graphs (where they agree) to the disordered setting, unimodular random graphs. In particular, we find that the Benjamini-Schramm locality of the critical density (a well-known open problem for transitive graphs) completely fails in the generality of unimodular random graphs.
A corollary to our positive results is that for any transitive graph with sub-exponential volume growth there is a sequence T_n of large girth bi-Lipschitz invariant subgraphs such that p_c(T_n)\to 1. It remains open whether this holds whenever the transitive graph has cost 1.
A conformally invariant growth process of SLE excursions. [arXiv:1601.05713 math.PR] With Hao Wu.
ALEA Lat. Am. J. Probab. Math. Stat. 15 (2018), 851-874. Paper in the journal.
We construct an aggregation process of chordal SLE(\kappa) excursions in the unit disk, starting from the boundary, growing towards all inner points simultaneously, invariant under all conformal self-maps of the disk. We prove that this conformal growth process of excursions, abbreviated as CGE(\kappa), exists iff \kappa\in [0,4), and that it does not create additional fractalness: the Hausdorff dimension of the closure of all the SLE(\kappa) arcs attached is 1+\kappa/8 almost surely. We determine the dimension of points that are approached by CGE(\kappa) at an atypical rate, and construct conformally invariant random fields on the disk based on CGE(\kappa).
Answering questions of Itai Benjamini, we show that the event of complete occupation in 2-neighbour bootstrap percolation on the d-dimensional box [n]^d, for d\geq 2, at its critical initial density p_c(n), is noise sensitive, while in k-neighbour bootstrap percolation on the d-regular random graph G_{n,d}, for 2\leq k\leq d-2, it is insensitive. Many open problems remain.
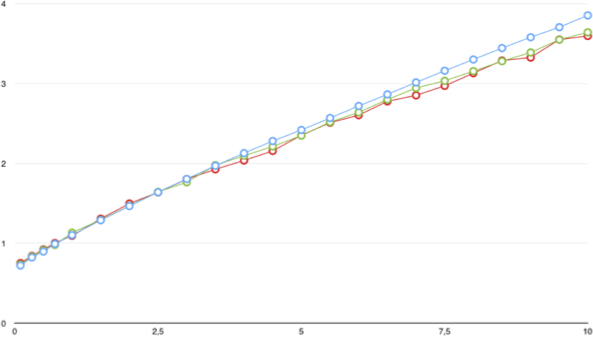
The tail of the crossing probability in near-critical percolation. An appendix to Daniel Ahlberg and Jeff Steif's Scaling limits for the threshold window: When does a monotone Boolean function flip its outcome? [arXiv:1405.7144 math.PR] Annales de l'Institut Henri Poincaré 53 (2017), 2135-2161. Paper in the journal.
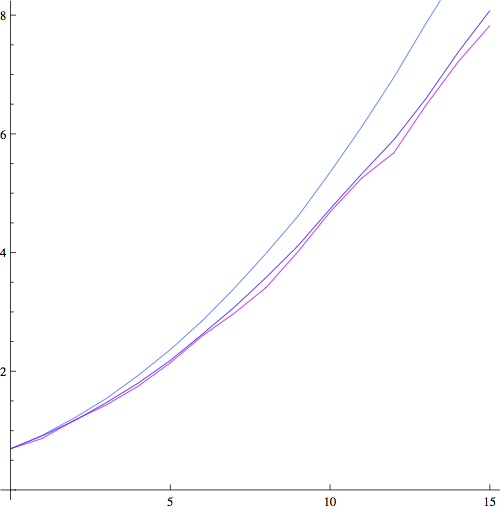
I answer a question of Ahlberg and Steif (2014) by finding the tail behaviour of the crossing probability in near-critical planar percolation. Interestingly, this superexponentially small behaviour is different from the case of dynamical percolation, where the analogous tail probability was proved to be at least exponential and at most superpolynomial by Hammond, Mossel and Pete (2012). The proof is simple, given the scale covariance established by Garban, Pete and Schramm (2013).
The function on the left shows simulation results for near-critical percolation, converging to t^{4/3}. After exponentiating, this is the superexponential tail computed in this paper. The function on the right is for dynamical percolation. Open problem: show that it is sublinear.
The scaling limits of the Minimal Spanning Tree and Invasion Percolation in the plane. [arXiv:1309.0269 math.PR] With Christophe Garban and Oded Schramm. Ann. Probab. 46 (2018), 3501-3557. Paper in the journal.
We prove that the Minimal Spanning Tree and the Invasion Percolation Tree on
a version of the triangular lattice in the complex plane have unique scaling
limits, which are invariant under rotations, scalings, and, in the case of the MST, also under translations. However, they are not expected to be conformally invariant. We also prove some geometric properties of the limiting MST. The topology of convergence is the space of spanning trees introduced by Aizenman, Burchard, Newman & Wilson (1999), and the proof relies on the existence and conformal covariance of the scaling limit of the near-critical percolation ensemble, established in our earlier works.
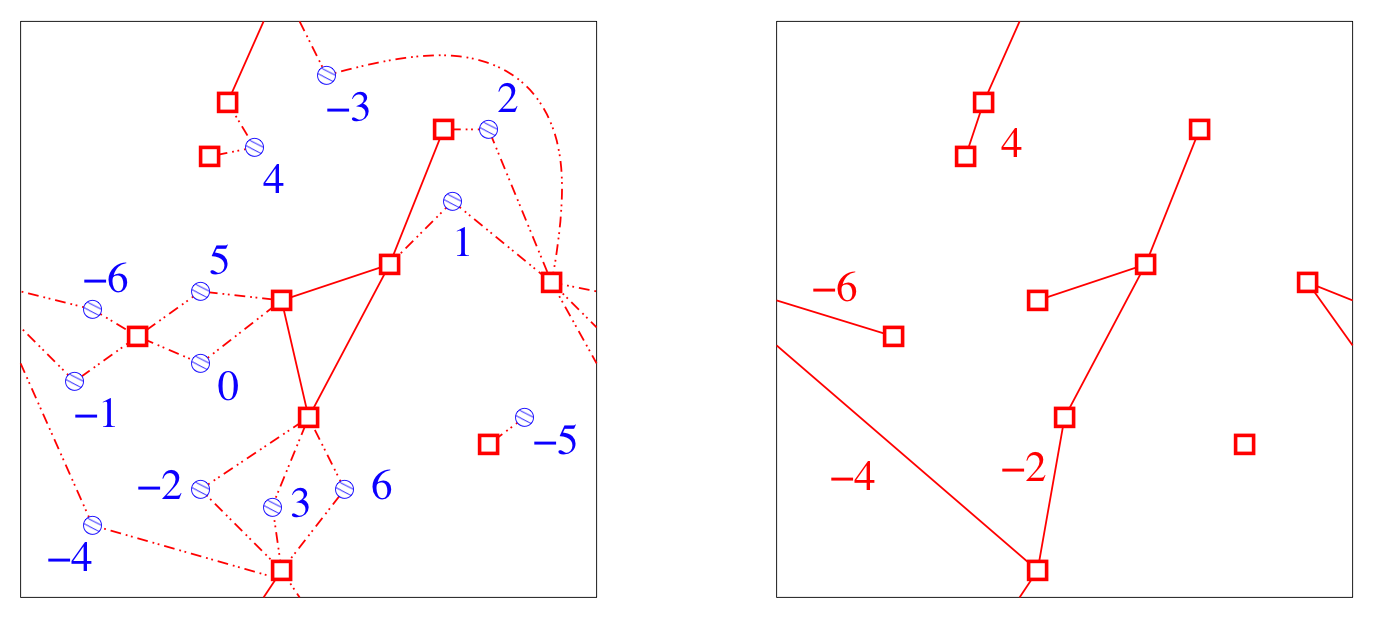
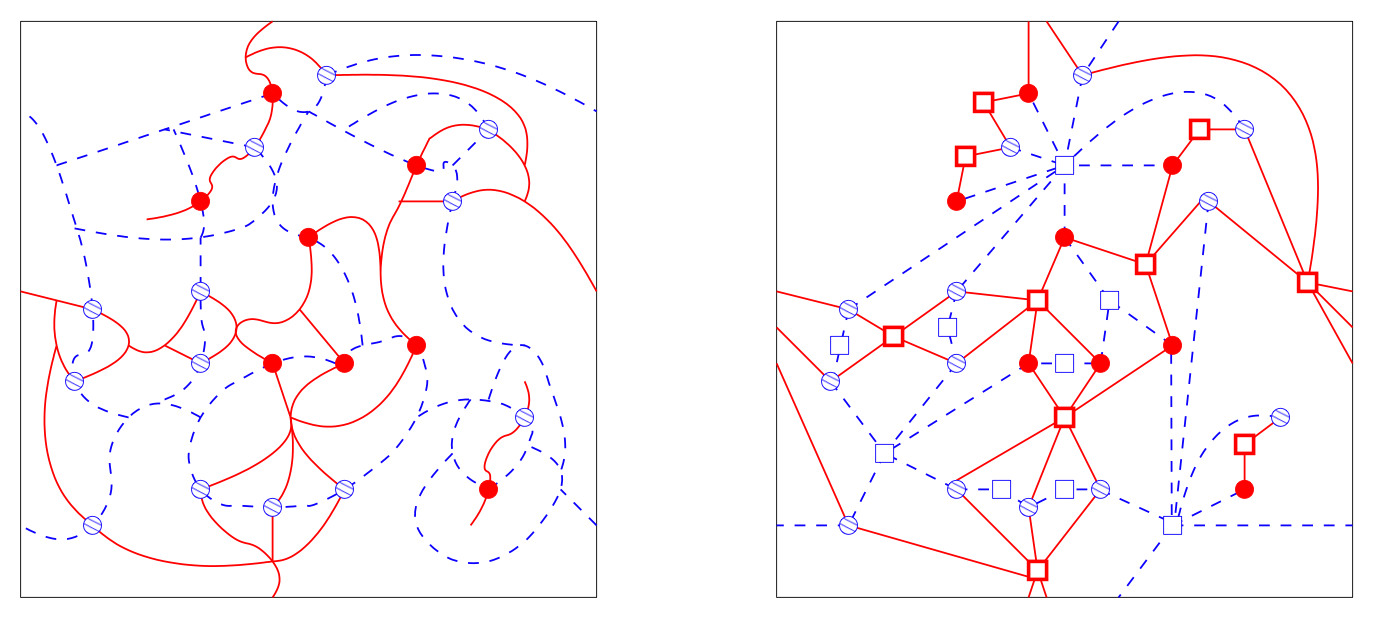
The pictures on the right show how a percolation configuration on a torus, with pivotals labelled according to the near-critical level at which they become open, gets undressed, all the way to its MST skeleton. The picture on the left is a piece of an invasion percolation tree.
We prove that near-critical percolation and dynamical percolation on the triangular lattice have a scaling limit as the mesh goes to 0, in the ``quad-crossing'' space of percolation configurations introduced by Schramm and Smirnov. The proof essentially proceeds by ``perturbing'' the scaling limit of the critical model, using the pivotal measures studied in our earlier paper. Markovianity and conformal covariance of these new limiting objects are also established.
Local time on the exceptional set of dynamical percolation, and the Incipient Infinite Cluster. [arXiv:1208.3826 math.PR] With Alan Hammond and Oded Schramm. Ann. Probab. 43 (2015), 2949-3005. Paper in the journal.
In dynamical critical site percolation on the triangular lattice or bond percolation on Z^2, we define and study a local time measure on the exceptional times at which the origin is in an infinite cluster. We show that at a typical time with respect to this measure, the percolation configuration has the law of Kesten's Incipient Infinite Cluster. In the most technical result of this paper, we show that, on the other hand, at the first exceptional time, the law of the configuration is different. We also study the collapse of the infinite cluster near typical exceptional times, and establish a relation between static and dynamic exponents, analogous to Kesten's near-critical relation.
Exit time tails from pairwise decorrelation in hidden Markov chains, with applications to dynamical percolation. [arXiv:1111.6618 math.PR] With Alan Hammond and Elchanan Mossel. Elect. J. Probab. 17 (2012), Article no. 68, 1-16. Paper in the journal.
Consider a reversible Markov process X_t at equilibrium and some event C (a subset of the state-space). We show that any decay of the pairwise correlation \P[ X_0,X_t \in C ] - \P[ X_0 \in C ]^2 implies a similar decay of the continual occurrence \P[ X_s \in C, for all s \in [0,t] ]. We provide examples showing that our results are often tight. Our results generalize the well-known Ajtai-Komlós-Szemerédi lemma about exit time tails in expanders, where there is an exponential pairwise decorrelation for any event.
Our main applications are to dynamical critical percolation. Let C be the left-right crossing event of a large box, and let us scale time so that the expected number of changes to C is order 1 in unit time. We show that the continual connection event has superpolynomial decay. Furthermore, on the infinite lattice without any time scaling, the first exceptional time with an infinite cluster appears with an exponential tail.
The near-critical planar FK-Ising model. [arXiv:1111.0144 math.PR] With Hugo Duminil-Copin and Christophe Garban. Comm. Math. Phys. 326 (2014), 1-35. Paper in the journal.
In the near-critical FK (or random cluster) model FK(p,q), in the q=2 Ising case, when we raise p near p_c (which corresponds to lowering the temperature in the Ising model), how do new edges appear? How fast does the system change from subcritical to supercritical?
Using conformal invariance techniques (Smirnov's fermionic observable), we determine the correlation length (critical window), more-or-less strengthening classical results of [Onsager 1944]. Furthermore, a striking phenomenon is highlighted, completely missing from the case of standard percolation, and seemingly not noted by physicists: the new edges arrive in a fascinating self-organized way, so that the critical window is shorter than what could be expected by the amount of pivotal edges at criticality.
Finally, for the heat-bath dynamics in critical random-cluster models, we conjecture that there is a regime of values of cluster-weights q where there exist macroscopic pivotals yet there are no exceptional times. These are the first natural models that are expected to be noise sensitive but not dynamically sensitive.
(Thanks to Vincent Beffara for the two Ising pictures above; inverse temperatures \beta=0.881374, the critical, and \beta=0.9.)
Pivotal, cluster and interface measures for critical
planar percolation. [arXiv:1008.1378 math.PR] With Christophe Garban and Oded Schramm. Journ. Amer. Math. Soc. 26 (2013), 939-1024.
Paper in the journal.
This work is the first in a series of papers devoted to the construction and study of scaling limits of dynamical and near-critical planar percolation and related objects like invasion percolation and the Minimal Spanning Tree. We show here that the counting measure on the set of pivotal points of critical site percolation on the triangular grid, normalized appropriately, has a scaling limit, which is a function of the scaling limit of the percolation configuration. We also show that this limit measure is conformally covariant, with exponent 3/4. Similar results hold for the counting measure on macroscopic open clusters (the area measure), and for the counting measure on interfaces (length measure).
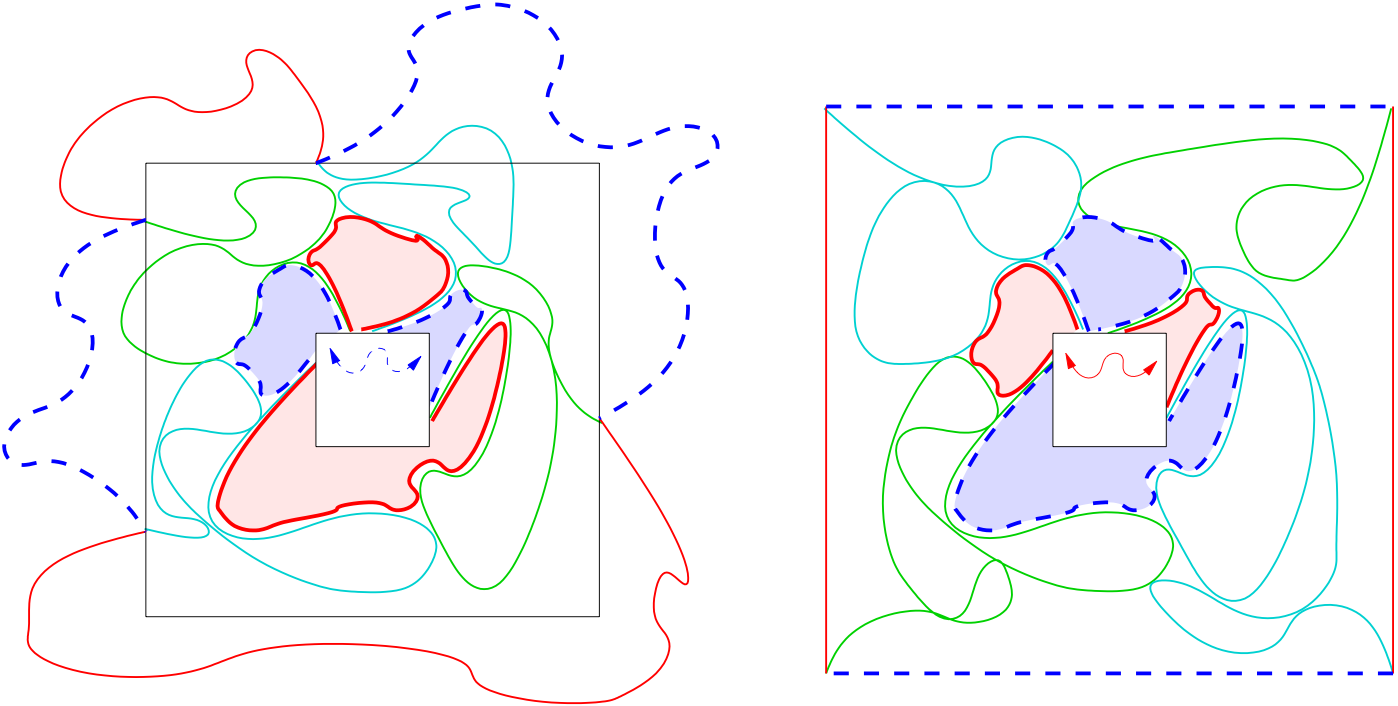
Since the aforementioned processes are very much governed by pivotal sites, the construction and properties of the "local time"-like pivotal measure are key results in this project. Another application is that the existence of the limit length measure on the interface is a key step towards constructing the so-called natural time-parametrization of the SLE(6) curve.
The proofs make extensive use of coupling arguments, based on the separation of interfaces phenomenon. This is a very useful tool in planar statistical physics, on which we included a self-contained Appendix. Simple corollaries of our methods include ratio limit theorems for arm probabilities and the rotational invariance of the two-point function.
The scaling limit of the Minimal Spanning Tree - a preliminary report. [arXiv:0909.3138 math.PR] With Christophe Garban and Oded Schramm. XVIth International Congress on Mathematical Physics (Prague, 2009), ed. P. Exner, pp. 475-480., World Scientific, Singapore, 2010.
This is a short (and somewhat informal) contribution to the proceedings of the Prague ICMP, written up by me. I describe how the recent proof of the existence and conformal covariance of the scaling limits of dynamical and near-critical planar percolation implies the existence and several topological properties of the scaling limit of the Minimal Spanning Tree, and that it is invariant under scalings, rotations and translations. However, we do not expect conformal invariance: I explain why not and what is missing for a proof. Of course, there will later be a proper paper on this subject, after we have finished the papers on the scaling limits of dynamical and near-critical percolation.
Scale-invariant groups. [arXiv:0811.0220v4 math.GR] With Volodymyr Nekrashevych. Groups, Geometry and Dynamics 5 (2011), 139-167. Paper in the journal.
For statistical mechanics on the Z^d lattice, it is very useful that the lattice can be tiled by large boxes, because: 1. each box looks locally like the infinite lattice; 2. the tiling graph on the boxes is again the same lattice. On what other groups are there such scale-invariant tilings? A natural guess is that it should have polynomial volume growth. This remains open, but we disprove a group-theoretical version of this conjecture, made by Itai Benjamini: we show that there are "scale-invariant groups" of exponential growth (and even non-amenable), e.g, the lamplighter group Z_2 wr Z, and the affine group over Z^d. We use some self-similar actions by these groups to prove this. We also construct scale-invariant tilings in the discrete Heisenberg group, using some particularly nice self-similar actions of the group. On the other hand, we show that torsion-free hyperbolic groups are not scale-invariant.
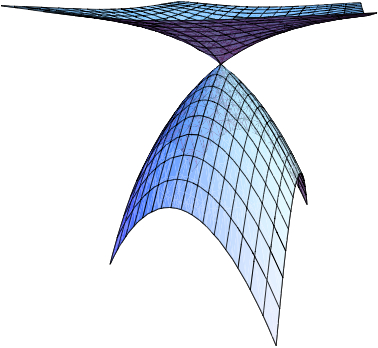Biased tug-of-war, the biased infinity Laplacian, and comparison with exponential cones.
[arXiv:0811.0208v3 math.AP]
With Yuval Peres and Stephanie Somersille. Calculus of Variations and Partial Differential Equations 38 (2010), 541-564. Paper in the journal.
Generalizing recent work of Peres, Schramm, Sheffield and Wilson, we apply the game random tug-of-war, played with a little bit biased coin, to prove existence and uniqueness results for the biased Infinity Laplacian PDE. The main tool to connect the game with the viscosity solutions of this degenerate PDE is comparison with exponential cones. The main difficulty compared to the unbiased case in PSSW comes from the fact that the connection to Absolutely Minimizing Lipschitz Extensions is lost.
The Fourier
spectrum of critical percolation. [arXiv:0803.3750v3 math.PR] With
Christophe Garban and Oded Schramm. Acta Mathematica 205 (2010), 19-104. Paper in the journal.
Crossing events in critical planar percolation are extremely sensitive to noise. This lets some very exceptional events occur in dynamical percolation. In this paper, we understand the Fourier-Walsh expansion of the characteristic functions of monotone crossing events quite precisely, and, using this, give exact quantitive descriptions of the noise- and dynamical sensitivity of the model. E.g., the set of exceptional times of dynamical critical site percolation on the triangular grid in which the origin percolates has Hausdorff dimension 31/36 a.s. Probably these are the most complex Boolean functions whose Fourier spectrum have been understood this well.
We show that the entropy of the sum of independent random variables can greatly differ from the entropy of their difference. The gap between the two entropies can be arbitrarily large. This holds for regular entropies as well as differential entropies. Our results rely heavily on a result of Ruzsa, who studied sums and differences of finite sets.
A note on percolation on Z^d: isoperimetric profile via exponential cluster repulsion. [arXiv:math.PR/0702474v4] Elect. Comm. Probab. 13 (2008), 377-392. Paper in the journal.
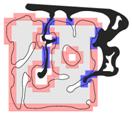
Large-scale geometric and random walk properties of the infinite supercritical percolation cluster on Z^d, for any p>p_c(Z^d), are basically the same as of the original lattice itself. Here I give a very simple proof of this important fact, which had been established in different forms in a series of papers by several authors during the past two decades. The main tool is a new large deviation result for supercritical percolation; I was quite surprised that one can still prove new results in such a classical field.
I also prove the survival of anchored isoperimetry in percolation on general graphs: for finitely presented groups with p close enough to 1, and for transient wedges in Z^3. In the latter, the main point is that the transience criterion of Terry Lyons turns out to imply Thomassen's criterion; this proof uses some simple entropy inequalities, similarly to how the Loomis-Whitney isoperimetric inequality can be proved using Shearer's inequality.
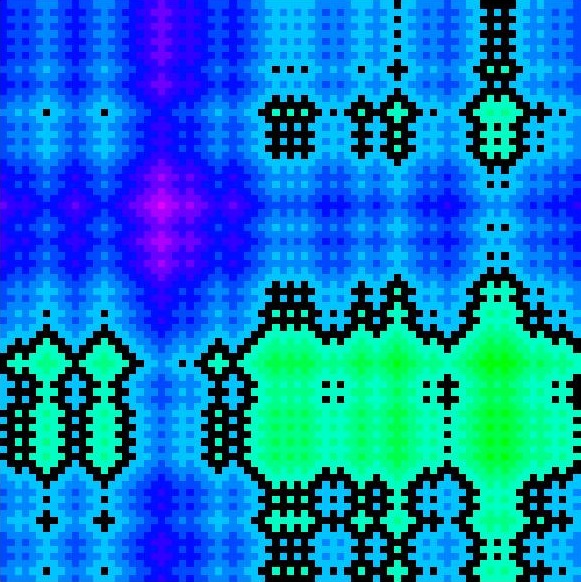Corner percolation on
Z^2 and the square root of 17. [arXiv:math.PR/0507457v4].
Annals of Probability 36 (2008), No. 5, 1711-1747.
Paper in the journal.
This is a dependent bond percolation model on Z^2, introduced by Bálint Tóth. At first sight, the model looks intractable, but I realized that it can be viewed as the set of level lines of a height function, which is just the sum of two independent random walks, hence has the Additive Brownian Motion as a scaling limit. The contour cycles are some strange products of simple random walk excursions. This made it possible to understand the model thoroughly, and find some surprising irrational critical exponents.
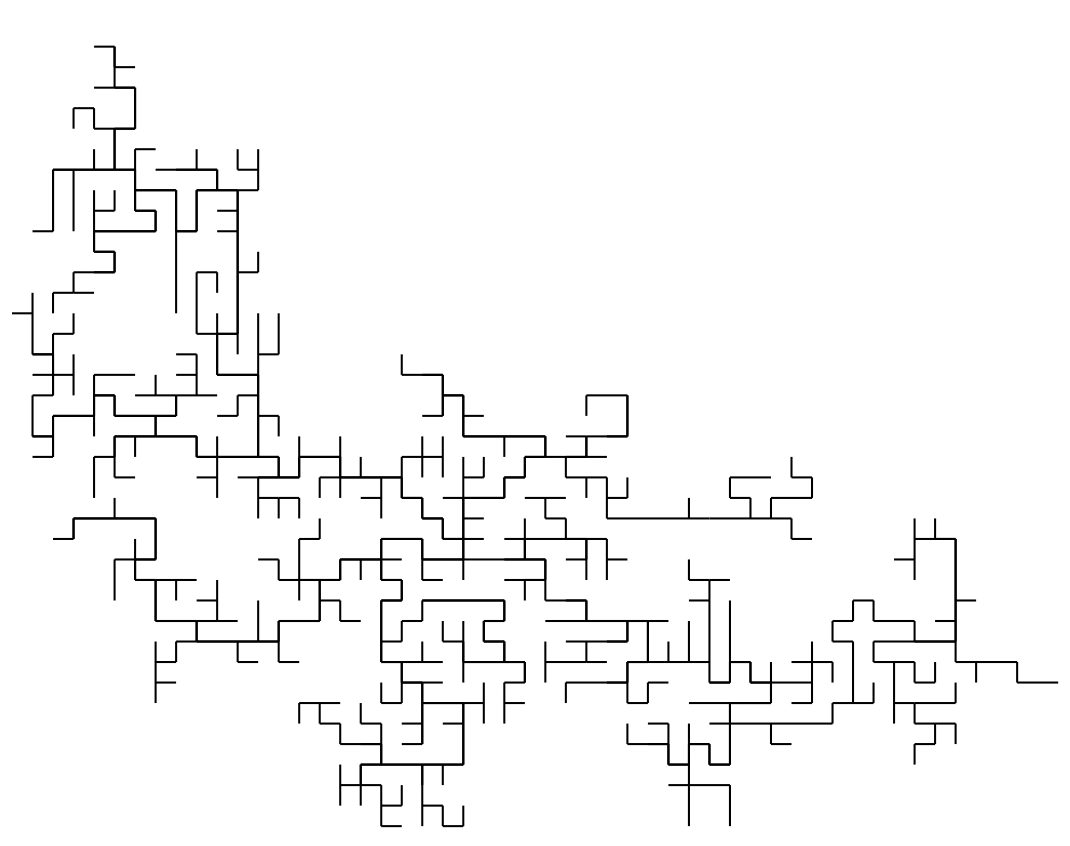
Here is a .pdf picture of a cycle of length 17996. It is worth zooming in. The "dimension" of this curve is (\sqrt{17}+1)/4=1.28..., a value coming from the solution of a singular sixth order ODE.
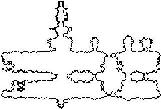
Corner percolation has inspired the definition of several other dependent percolation models with linear entropy: Itai Benjamini's trixor, Omer Angel's odd-trixor, my quaxor. According to computer simulations, odd-trixor and quaxor have the same scaling limit as independent percolation, hence are conformally invariant!
Here are some colourful slides, summarizing the many exciting open problems: Corner, trixor, odd-trixor, quaxor: Linear entropy planar percolation models without and with (conjectured) conformal invariance. This is a large pdf file (6 MB).
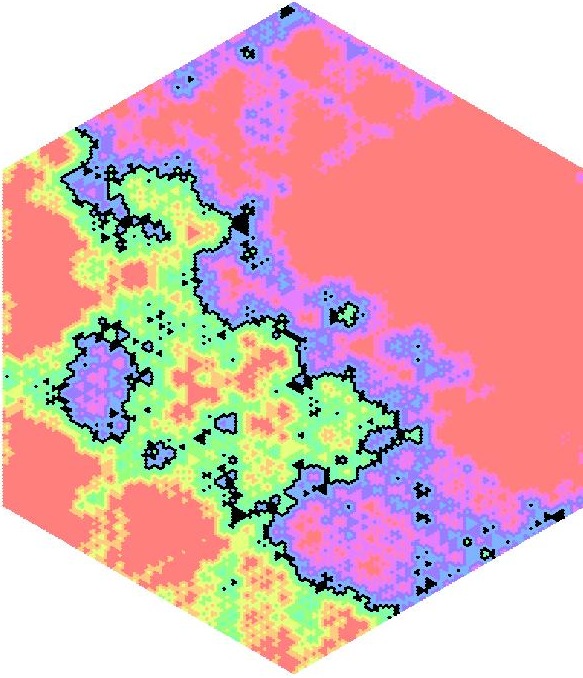
Critical percolation
on certain non-unimodular graphs. [arXiv:math.PR/0501532v3] With
Yuval Peres and Ariel Scolnicov.
New York Journal of Mathematics 12 (2006), 1-18.
Paper in the journal.
An important conjecture in percolation theory is that almost surely no infinite cluster exists in critical percolation on any transitive graph for which the critical probability is less than 1. Earlier work has established this for the amenable cases Z^2 and Z^d for large d, as well as for all non-amenable graphs with unimodular automorphism groups. We show that the conjecture holds for the basic classes of non-amenable graphs with non-unimodular automorphism groups: for decorated trees and the non-unimodular Diestel-Leader graphs. We also show that the connection probability between two vertices decays exponentially in their distance. Finally, we prove that critical percolation on the positive part of the lamplighter group has no infinite clusters.
Bootstrap percolation on infinite trees and non-amenable groups. [arXiv:math.PR/0311125v3] With József Balogh and Yuval Peres. Combinatorics, Probability and Computing, 15 (2006), no. 5, 715-730. Paper in the journal
Bootstrap percolation on an arbitrary graph G has a random Bernoulli(p) initial configuration of occupied sites and a deterministic spreading rule with a fixed parameter k: if a vacant site has at least k occupied neighbors at a certain time step, then it becomes occupied in the next step. The critical probability p(G,k) is the infimum of those values of p for which the process achieves complete occupation with positive probability. This process is well-studied on Z^d; here we investigate it on infinite trees and non-amenable Cayley graphs.
On general trees we describe the basic behaviour of the process in terms of the branching number of the tree, and find e.g. a surprising discontinuity: if k>br(T), then the critical probability is 1, while it is 1-1/k on the k-ary tree. On a d-regular tree, the critical probability is approximately k/d. We also prove that on any 2k-regular non-amenable graph, the critical probability for the k-rule is strictly positive.
An open question: is a group amenable if and only if for every Cayley graph G and spreading rule k, we have that p(G,k) is either 0 or 1? Known for Z^d on one hand, and for non-amenable groups with a free subgroup on two generators on the other.
Anchored expansion, percolation and speed. [arXiv:math.PR/0303321] Main text by Dayue Chen and Yuval Peres, appendix by myself. Annals of Probability, 32 (2004) no. 4, 2978-2995. Paper in the journal.
Benjamini, Lyons and Schramm (1999) considered properties of an infinite
graph G, and the simple random walk on it, that are preserved by random
perturbations. In this paper we solve several problems raised by those
authors. The anchored expansion constant is a variant of the Cheeger
constant; its positivity implies positive lower speed for the simple
random walk, as shown by Virág (2000). We prove that if G has a
positive anchored expansion constant then so does every infinite cluster
of independent percolation with parameter p sufficiently close to 1; a
better estimate for the parameters p where this holds is in the appendix.
We also show that positivity of the anchored expansion constant is
preserved under a random stretch if, and only if, the stretching law has
an exponential tail. We then study simple random walk in the infinite
percolation cluster in Cayley graphs of certain amenable groups known as
``lamplighter groups''. We prove that zero speed for random walk on a lamplighter
group implies zero speed for random walk on an infinite cluster, for any
supercritical percolation parameter p. For p large enough, we also
establish the converse.
Variations of the method of the Appendix are very useful in studying isoperimetric inequalities and random walks on percolation clusters of general graphs, including the classical case of Z^d. See my paper above on exponential cluster repulsion and the isoperimetric profile of percolation clusters of Z^d.
The Schinzel hypothesis claims (but it seems hopeless to prove) that any irreducible Q[x] polynomial without a constant factor assumes infinitely many prime values at integer places. On the other hand, it is easy to see that a reducible Q[x] polynomial can have only finitely many such places. In this paper we prove that a reducible Z[x] polynomial of degree n can have at most n+2 such places, and there exist examples with n+1 places. If the Schinzel hypothesis and the k-prime-tuple conjecture are true, then there are also polynomials with n+2 such places. (For n=4 or 5 the maximum possible value is 8.) If a Z[x] polynomial is the product of two non-constant integer-valued Q[x] polynomials, then there are at most 1.87234...n+o(n) such places. Even in this case, the number of integer places with positive prime values is at most n. More generally, if f=gh \in R[x] is a product of two non-constant real polynomials, then the number of real places x such that |g(x)|=1 or |h(x)=1|, while f(x)>1, is at most n. For a natural complex version of this statement we give a counterexample.
Random disease on the square grid. With József Balogh. Random Structures and Algorithms 13 (1998), 409-422. Also in .pdf.
Occupy each square of an n-by-n board independently with probability p(n), then take a deterministic spreading rule, the most interesting case being the following: if a square has at least two occupied neighbors at some time step, then it becomes occupied in the next step. How big does p(n) have to be to occupy the whole board with high probability? The main result of the paper is the almost exact determination of this threshold function. Further investigations are included about the general random and deterministic cases.
This model turned out to be already known as bootstrap percolation, and our main result was already proven by Aizenman and Lebowitz in 1988. Thus, I recommend looking at the expanded version, my undergrad thesis at the Bolyai Institute.