Next: Diszkrét változók feltételes várható Up: A feltételes várható érték Previous: A feltételes várható érték Tartalomjegyzék
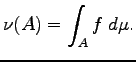
Az
A fenti tételre gondolhatunk például úgy, hogy
![]() mérhető térnek vesszük például
a három dimenziós valós teret a (Lebesgue-)mérhető halmazokkal, valamint
mérhető térnek vesszük például
a három dimenziós valós teret a (Lebesgue-)mérhető halmazokkal, valamint
![]() mértéknek vesszük
a mérhetők közönséges térfogatát. A
mértéknek vesszük
a mérhetők közönséges térfogatát. A
![]() mértéknek vehetjük például az elektromos
töltést, amely minden mérhetőn meg van adva, és pozitív, negatív értéket egyaránt felvehet.
Ekkor
mértéknek vehetjük például az elektromos
töltést, amely minden mérhetőn meg van adva, és pozitív, negatív értéket egyaránt felvehet.
Ekkor
![]() a töltéssűrűség lesz. Egy pontban kiszámolni úgy lehet, hogy
veszünk a pont körül kis (térfogatú) halmazokat és megnézzük, hogy ebben a halmazban mennyi az
egységnyi térfogatra eső töltés mennyisége, ami a halmazra eső töltés, és a térfogat,
vagyis
a töltéssűrűség lesz. Egy pontban kiszámolni úgy lehet, hogy
veszünk a pont körül kis (térfogatú) halmazokat és megnézzük, hogy ebben a halmazban mennyi az
egységnyi térfogatra eső töltés mennyisége, ami a halmazra eső töltés, és a térfogat,
vagyis
![]() és
és
![]() hányadosa. Ezután határátmenetet végzünk, amint a térfogat tart nullához.
Ez egy közönséges derivált. Ez a tény is mutatja a
hányadosa. Ezután határátmenetet végzünk, amint a térfogat tart nullához.
Ez egy közönséges derivált. Ez a tény is mutatja a
![]() jelölés jogosságát.
jelölés jogosságát.
Ezek után világos, hogy ezt a függvényt a térfogat, azaz
![]() szerint integrálva megkapjuk az
adott halmaz töltését, vagyis
szerint integrálva megkapjuk az
adott halmaz töltését, vagyis
![]() szerinti mértékét. Lehetnek olyan pozitív térfogatú,
szerinti mértékét. Lehetnek olyan pozitív térfogatú,
![]() mértékű részek, melyeknek nincs töltése, azaz
mértékű részek, melyeknek nincs töltése, azaz
![]() mértéke 0
, ezek pontjaiban
mértéke 0
, ezek pontjaiban ![]() értéke 0
kell
legyen. Olyan 0
térfogatú részek, melyek nem 0
töltéssel rendelkeznek viszont nem lehetnek, mert
ezen integrálva a
értéke 0
kell
legyen. Olyan 0
térfogatú részek, melyek nem 0
töltéssel rendelkeznek viszont nem lehetnek, mert
ezen integrálva a
![]() mértéket nullát kapnánk. Tehát világos, hogy a
mértéket nullát kapnánk. Tehát világos, hogy a
![]() mértéknek a
mértéknek a
![]() mértékre vonatkozó abszolút folytonossága szükséges. A
mértékre vonatkozó abszolút folytonossága szükséges. A
![]() mérték
mérték ![]() -végessége többek
között azt is megköveteli, hogy minden pont benne legyen egy véges mértékű mérhetőben. A két feltétel
az egyszerűbb esetekben azt garantálja, hogy se nullával, se végtelennel ne kelljen osztani.
-végessége többek
között azt is megköveteli, hogy minden pont benne legyen egy véges mértékű mérhetőben. A két feltétel
az egyszerűbb esetekben azt garantálja, hogy se nullával, se végtelennel ne kelljen osztani.
Az
![]() halmazrendszer bizonyos
halmazrendszer bizonyos
![]() részhalmazának elemein kell integrálni az
részhalmazának elemein kell integrálni az
![]() valószínűségi változót, vagyis venni a várható értékét, amivel egy mértéket kapunk a
valószínűségi változót, vagyis venni a várható értékét, amivel egy mértéket kapunk a
![]()
![]() -algebrán, ez a várható értékből származó mérték. Ez a mérték egy előjeles mérték.
-algebrán, ez a várható értékből származó mérték. Ez a mérték egy előjeles mérték.
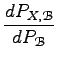
Radon-Nikodym deriváltat nevezzük az
Az
![]() által generált
által generált ![]() -algebra az a legszűkebb
-algebra az a legszűkebb ![]() -algebra, melyre nézve
-algebra, melyre nézve
![]() mérhető. Tehát valós esetben például az
mérhető. Tehát valós esetben például az
![]() eseménytér beli
eseménytér beli
![]() alakú halmazok által generált
alakú halmazok által generált
![]() -algebra.
A
-algebra.
A
![]() jelölés mellett a
jelölés mellett a
![]() jelölés is jogos, mert a feltételes várható érték nem
függ az
jelölés is jogos, mert a feltételes várható érték nem
függ az
![]() valószínűségi változó értékeitől, sem attól, hogy melyik halmazba mekkora valószínűséggel
esik az értéke, hanem csak a
valószínűségi változó értékeitől, sem attól, hogy melyik halmazba mekkora valószínűséggel
esik az értéke, hanem csak a
![]()
![]() -algebrától, hiszen a definícióban csak ez szerepel.
A feltételes várható érték mint sűrűségfüggvény nem teljesen egyértelmű,
de két ilyen sűrűségfüggvény csak nullmértékű halmazon térhet el.
Ezért ha egy adott
-algebrától, hiszen a definícióban csak ez szerepel.
A feltételes várható érték mint sűrűségfüggvény nem teljesen egyértelmű,
de két ilyen sűrűségfüggvény csak nullmértékű halmazon térhet el.
Ezért ha egy adott
![]() halmazon a sűrűséget integráljuk, bármelyik sűrűségfüggvényt
használjuk is, a
halmazon a sűrűséget integráljuk, bármelyik sűrűségfüggvényt
használjuk is, a
![]() halmaz ugyanazon előjeles súlyát kapjuk meg.
Tehát tetszőleges feltételes várható értékkel teljesül a következő egyenlőség:
halmaz ugyanazon előjeles súlyát kapjuk meg.
Tehát tetszőleges feltételes várható értékkel teljesül a következő egyenlőség:
Az első várható értékben csak a
Temesi Róbert 2010-08-16