Diszkrét változók feltételes várható értéke

A feltételes várható érték meghatározásakor a legegyszerűbb eset, ha a valószínűségi változók diszkrétek. Ha $\boldsymbol X$ és $\boldsymbol Y$ diszkrét valószínűségi változók, akkor létezik az $\boldsymbol E(\boldsymbol X)$ várható érték. Valamint létezik tetszőleges $y$ mellett az $\boldsymbol X$ változó feltételes eloszlása az $\boldsymbol Y\hskip -.75ex = y\,$ eseményre nézve, amennyiben $\boldsymbol P(\,\boldsymbol Y\hskip -.75ex=y\,) > 0$ . Az $\boldsymbol X$ változó ezen feltételes eloszlása melletti várható értékét nevezzük az $\boldsymbol X$ változó $\boldsymbol Y=y$ eseményre vett feltételes várható értékének, és az $\boldsymbol E(\boldsymbol X\vert\boldsymbol Y=y)$ jelölést használjuk rá.

Az $\boldsymbol Y$ változó minden olyan értékére, amelyre $\boldsymbol P(\boldsymbol Y=y)>0$ az $\boldsymbol Y=y$ eseményhez hozzárendelhetjük az $\boldsymbol E(\boldsymbol X\vert\boldsymbol Y=y)$ feltételes várható értéket. Megtehetjük, hogy nem csak az $\boldsymbol Y=y$ eseményhez, mint halmazhoz rendeljük hozzá a hozzá tartozó feltételes várható értéket, hanem hozzárendeljük a halmaz minden eleméhez, azaz minden olyan $\boldsymbol\Omega$ eseménytérbeli $\omega$ elemhez, mely az $\boldsymbol Y=y$ halmazhoz tartozik. Így minden olyan $\boldsymbol\Omega$ beli $\omega$ elemhez, mely valamely $y$ értékre egy pozitív valószínűségű $\boldsymbol Y=y$ esemény eleme, hozzárendelhető a megfelelő feltételes várható érték. Az olyan $\omega$ elemekhez, melyekhez a fenti módon nem tudunk feltételes várható értéket rendelni, rendelhetünk tetszőleges értéket. Ez többértelműséghez vezet, de csak egy nulla valószínűségű esemény elemein nem határoztuk meg egyértelműen a hozzárendelt értéket. Mivel minden $\boldsymbol\Omega$ beli $\omega$ elemhez hozzárendeltünk egy számot, így egy valószínűségi változót kaptunk. Ez a valószínűségi változó az $\boldsymbol X$ valószínűségi változó $\boldsymbol Y$ valószínűségi változóra vett, fent definiált, $\boldsymbol E(\boldsymbol X\vert\boldsymbol Y)$ jelöléssel jelölt feltételes várható értéke. Figyeljük meg, hogy itt már nem egy esemény, hanem az $\boldsymbol Y$ változó szerepel a feltételben. Ebben az esetben jól látszik, hogy a feltételes várható értéknek, mint valószínűségi változónak a meghatározásánál nem játszik szerepet az, hogy az $\boldsymbol Y$ változó konkrétan milyen értékeket vesz fel, hanem csak az számít, hogy az $\boldsymbol Y$ által felvett értékeknek mely halmazok az ősei az $\boldsymbol\Omega$ eseménytérben. Illetve kicsit általánosabban szólva csak az $\boldsymbol Y$ által generált $\sigma$ -algebra számít. Esetünkben ez a $\sigma$ -algebra az $y$ értékek ősei, vagyis az $\boldsymbol Y=y$ események által generált $\sigma$ -algebra. Az $\boldsymbol Y$ értékei csak annyiban számítanak, hogy általuk tudjuk megnevezni, hogy a feltételes várható érték, mint valószínűségi változó mely halmazon felvett értékeiről beszélünk. Jól látszik, hogy logikus úgy gondolnunk a feltételes várható értékre, ha a feltételben egy valószínűségi változó áll, mint a valószínűségi változó által generált $\sigma$ -elgebrára mint feltételre vett feltételes várható értékre. Ha ezt a legszűkebb $\sigma$ -algebrát $\boldsymbol{\EuScript B}$ jelöli, akkor tehát használhatjuk a következő jelölést is: $\boldsymbol E(\boldsymbol X\vert\boldsymbol{\EuScript B})$ .

Az előbb definiált feltételes várható érték valóban megfelel a feltételes várható érték definíciójának. Most tehát a $\boldsymbol{\EuScript B}$ $\sigma$ -algebra az $\boldsymbol\Omega$ beli $\boldsymbol Y=y$ események által generált $\sigma$ -algebra. Egy olyan $\boldsymbol Y=y$ halmaz elemein, melyre $\boldsymbol P(\boldsymbol Y=y)>0$ a feltételes várható értéket konstans

$$\sum_{\{x\vert\boldsymbol P(\boldsymbol X=x)>0\}} x\boldsymbol P(\boldsymbol X=x\vert\boldsymbol Y=y)$$

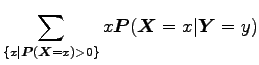
értéknek definiáltuk, mivel ez pont az $\boldsymbol X$ feltételes eloszlása szerinti várható értéke. Az $\boldsymbol\Omega$ többi, egy $\boldsymbol D$ halmazt alkotó elemén definiáljuk például nullának. Ez tehát az $\boldsymbol E(\boldsymbol X\vert\boldsymbol{\EuScript B})$ változó. Erre teljesülnie kell tetszőleges $\boldsymbol B\in \boldsymbol{\EuScript B}$ halmaz esetén a

$$\boldsymbol P_{\boldsymbol X, \boldsymbol{\EuScript B}}(\boldsymb... ...ymbol X\vert\boldsymbol{\EuScript B}) d\boldsymbol P_{\boldsymbol{\EuScript B}}$$

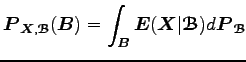
egyenletnek, amint azt a definíció a Radon-Nikodym tétel alapján megköveteli. Tekintsünk most el a $\boldsymbol D$ halmaztól, mivel az egyenlet mindkét oldalán egy integrál van, és ezek értéke egy nullmértékű halmazon $0.$ Legyenek az $\boldsymbol X$ változó értékeinek ősei az ${\boldsymbol A_i}$ halmazok, az $\boldsymbol Y$ változó értékeinek ősei a ${\boldsymbol B_j}$ halmazok. Ekkor a fenti ${\boldsymbol B}$ halmaz előáll ${\boldsymbol B_j}$ halmazok uniójaként, azaz

$${\boldsymbol B}=\bigcup_j {\boldsymbol B_j},$$

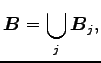
valamint mivel a ${\boldsymbol B_j}$ halmazok tartoznak a szűkebb $\sigma$ -algebrába, ezért ezek felírhatóak valamely ${\boldsymbol A_i}$ halmazok uniójaként, azaz

$$\boldsymbol B_j=\bigcup_i\bf A_{ij}$$

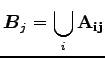
Így a baloldal értéke

$$\boldsymbol E(\boldsymbol X{\cal I}(\boldsymbol B)) = \boldsymbol... ...um_j {\cal I}(\bf A_{ij})\right)= \sum_i\sum_jx_{ij} \boldsymbol P(\bf A_{ij}).$$

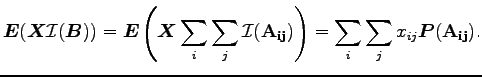
Mivel $\bf A_{ij}\subset B_j$ , ezért $\boldsymbol P(\bf A_{ij}\vert B_j)=\boldsymbol P(A_{ij})/\boldsymbol P(B_j).$ Ezért jobboldal értéke

$$\sum_j\left(\sum_i x_{ij}{{\boldsymbol P(\bf A_{ij})}\over{\bolds... ...)}}\right)\boldsymbol P(\bf B_j)= \sum_i\sum_jx_{ij} \boldsymbol P(\bf A_{ij}).$$

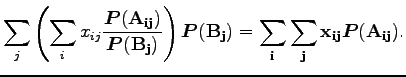
Tehát az így definiált feltételes várható érték tényleg eleget tesz a feltételnek.