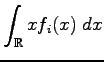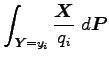Ugyanaz, mint az előző eset. Ugyanis ha
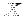 folytonos valószínűségi változó
folytonos valószínűségi változó 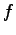 sűrűségfüggvénnyel,
sűrűségfüggvénnyel,
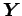 diszkrét valószínűségi változó, és az
diszkrét valószínűségi változó, és az
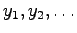 értékeket veheti fel és
értékeket veheti fel és
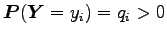 , akkor léteznek tetszőleges
, akkor léteznek tetszőleges
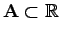 mérhető halmazra a
mérhető halmazra a
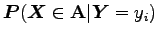 feltételes valószínűségek, melyeknek szintén létezik sűrűsége.
Ezt a feltételes sűrűséget jelölje
feltételes valószínűségek, melyeknek szintén létezik sűrűsége.
Ezt a feltételes sűrűséget jelölje 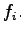 Így az
Így az
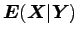 feltételes várható értéket definiálhatjuk egy
feltételes várható értéket definiálhatjuk egy 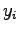 ősein az
ősein az
integrál értékének. Ez nem más, mint a definíció szerinti
integrál.
Tulajdonképpen azt is mondhattuk volna, hogy adva van egy az 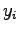 pontokra koncentrált számláló
mérték az
pontokra koncentrált számláló
mérték az 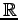 téren, azaz ezeknek a pontoknak
téren, azaz ezeknek a pontoknak 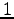 a valószínűsége, és minden más (Lebesgue)
mérhető halmaznak annyi a mértéke, amennyi
a valószínűsége, és minden más (Lebesgue)
mérhető halmaznak annyi a mértéke, amennyi 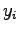 beleesik. Valamint az
beleesik. Valamint az 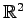 valós síkon adva
van a fenti számláló mértéknek, és a Lebesgue mértéknek a szorzata. Tehát
valós síkon adva
van a fenti számláló mértéknek, és a Lebesgue mértéknek a szorzata. Tehát 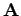 és
és 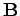 mérhető halmaz
Descartes szorzatának a mértéke
mérhető halmaz
Descartes szorzatának a mértéke 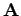 számláló mértékének és
számláló mértékének és 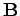 Lebesgue mértékének a szorzata.
Speciálisan egy téglalap mértéke az oldalak mértékeinek szorzata, az egyik oldalnál a számláló, a másik
oldalnál a Lebesgue mértéket használva. A többi, nem Descartes szorzat alakú halmaznak a mértéke,
pedig a köré írható Descartes szorzat alakú halmazok mértékének infimuma, a szokásos módon.
Ekkor az
Lebesgue mértékének a szorzata.
Speciálisan egy téglalap mértéke az oldalak mértékeinek szorzata, az egyik oldalnál a számláló, a másik
oldalnál a Lebesgue mértéket használva. A többi, nem Descartes szorzat alakú halmaznak a mértéke,
pedig a köré írható Descartes szorzat alakú halmazok mértékének infimuma, a szokásos módon.
Ekkor az
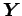 változónak létezik a sűrűsége a hozzá tartozó, fent definiált számláló mérték szerint,
és a sűrűség értéke az
változónak létezik a sűrűsége a hozzá tartozó, fent definiált számláló mérték szerint,
és a sűrűség értéke az 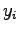 pontban
pontban 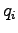 . Létezik
. Létezik
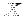 és
és
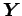 együttes sűrűsége is a szorzat
mérték szerint. Egy
együttes sűrűsége is a szorzat
mérték szerint. Egy 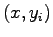 pontban az értéke éppen
pontban az értéke éppen
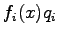 . Amint két folytonos változó esetén
később látjuk, itt is tulajdonképpen az együttes sűrűségfüggvény és a feltételben adott változó
sűrűségfüggvényének hányadosa szerint kell integrálni
. Amint két folytonos változó esetén
később látjuk, itt is tulajdonképpen az együttes sűrűségfüggvény és a feltételben adott változó
sűrűségfüggvényének hányadosa szerint kell integrálni 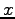 -et azokra az
-et azokra az 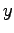 pontokra, melyekre
pontokra, melyekre
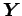 sűrűségfüggvénye nem nulla, ez a fent felírt integrál.
sűrűségfüggvénye nem nulla, ez a fent felírt integrál.
Temesi Róbert
2010-08-16
![]() folytonos valószínűségi változó
folytonos valószínűségi változó ![]() sűrűségfüggvénnyel,
sűrűségfüggvénnyel,
![]() diszkrét valószínűségi változó, és az
diszkrét valószínűségi változó, és az
![]() értékeket veheti fel és
értékeket veheti fel és
![]() , akkor léteznek tetszőleges
, akkor léteznek tetszőleges
![]() mérhető halmazra a
mérhető halmazra a
![]() feltételes valószínűségek, melyeknek szintén létezik sűrűsége.
Ezt a feltételes sűrűséget jelölje
feltételes valószínűségek, melyeknek szintén létezik sűrűsége.
Ezt a feltételes sűrűséget jelölje ![]() Így az
Így az
![]() feltételes várható értéket definiálhatjuk egy
feltételes várható értéket definiálhatjuk egy ![]() ősein az
ősein az