Általában megkövetelhetjük, hogy a kövezésnek egy
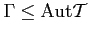 szimmetriacsoportja változatlanul hagyja a kövezés
kombinatorikus
struktúráját, így a baricentrikus felbontást is. Azaz
szimmetriacsoportja változatlanul hagyja a kövezés
kombinatorikus
struktúráját, így a baricentrikus felbontást is. Azaz
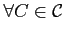 esetén
esetén
 igaz:
igaz:
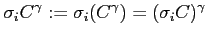 |
(4) |
Jelöljük
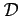 -vel a szimmetria csoport szerinti
szimplex-pályák halmazát:
-vel a szimmetria csoport szerinti
szimplex-pályák halmazát:
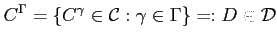 |
(5) |
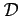 -n is jól értelmezett a szomszédsági operáció a
(4) egyenlőség miatt, azaz
-n is jól értelmezett a szomszédsági operáció a
(4) egyenlőség miatt, azaz
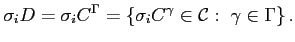 |
(6) |
Boroczki Lajos
2007-05-29