D-szimbólum szerkesztése egy adott térkitöltésből

Ebben a fejezetben a következő problémára adunk egy választ: Ha adott egy tetszőleges d-dimenziós euklideszi térkitöltés vagy kövezés (később bármelyik térben) a fundamentális tartományával, akkor milyen topologikus osztályba sorolhatjuk, azaz mik a legfontosabb tulajdonságai egy euklideszi rácspoliédernek (pl. az egyszerű hasonlósági operációval egymásba vihető rácsok nem nevezhetőek lényegesen különbözőknek.) Ilyen fontos jellemzők pl. hogy a fundamentális tartománynak hány zászlós alakzata, azaz hány baricentrikus szimplexe van (ezt pongyolán fogalmazva alaknak hívhatjuk) illetve hogy egy-egy k-dimenziós oldallapját hány szomszédos tartomány veszi körül.

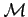Először röviden ismertetjük a baricentrikus felbontást. Az így nyert szimplexekre bevezetünk szomszédsági operációkat. A térkitöltés szimmetria csoportja alapján szimplex-pályákat határozunk meg. Bevezetjük a (d-2)-lapok¹ körüli forgásrendek leírására az $\mathcal{R}$ és $\mathcal{M}$ mátrix-függvényeket. A baricentrikus szimplex-felbontás miatt fellép néhány szükséges feltétel a D-szimbólum operációira, ezeket részletezzük. Végül két példán keresztül végighaladunk a fenti lépéseken.