---

Lesson 7
Column generation

---

I. Primal and Dual Linear Programming models

Let's remind ourselves about the Primal and Dual Linear Programming models, and the Strong Duality Theorem: $$\text{(P)}\begin{cases}\max_x(c^T x) \\ Ax \le b \\ x \ge 0\end{cases} \quad\quad \text{(D)}\begin{cases}\min_y(b^T y) \\ A^T y \ge c \\ y \ge 0\end{cases}$$ The Strong Duality Theorem states that $$\max_x (c^T x) = \min_y (b^T y)$$ Strong duality example in Mosel: How to obtain the dual and the activity of each constraint:

Download the Lesson7_DualExample.mos Mosel model from here

II. The Cutting Stock problem

We are running a paper mill that produces fixed size sheets of paper (94x1 m). We have several orders to fulfil: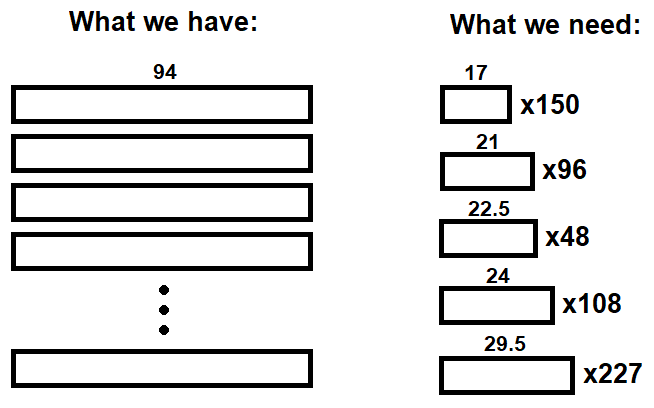


We would like to minimize the number of sheets used (minimize the overall losses).

Problem: There are too many possible patterns. For example:


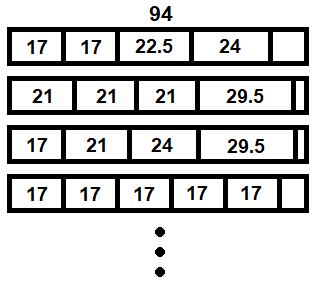
We can assume that the pieces cut are in increasing order of length.

We call patterns that only consist of 1 type of cut and use as much of the paper as possible "simple patterns":

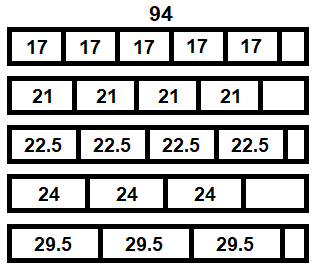
III. Heuristic solution

Idea:

1. Start with only the simple patterns and solve the problem.
2. Generate some pattern heuristically that improve the solution.
3. Solve the problem with the new set of patterns. Go to 2.

III./1. Exercise 1

a) Give a theoretical lower bound on the number of sheets we need!
b) Suggest at least 3 more patterns that use almost all of the sheet!
c) Give a theoretical lower and upper bound for the number of possible patterns! (Both sides should belong to the same family of functions.) How feasible is it to generate all possible patterns?

III./2. Heuristic pattern generation algorithm (S. Heipcke, 2002)

1. Calculate a theoretical lower bound of sheets needed like in exercise 1/a).
2. Set an error bound and/or a max iteration count.
3. Using only simple patterns, find the optimal solution. If it matches the theoretical optimum, then we are done. Otherwise go to 4.
4. "Assignment": Assign 1 order per sheet.
5. "Fill": Find the least filled sheet. If it's possible to add to it, then add the largest possible order size to it. Repeat until no more items can be added to any sheet. Add the new configurations to the possible patterns.
6. Solve the problem with the new set of patterns. If the result is at most the error bound away from the theoretical optimum, then we're done. If not, go to 7.
7. "Randomization": Generate a random pattern. (Choose a random order size. As long as it fits, add it to the pattern.)
8. Solve the problem with the new set of patterns. If the result is at most the error bound away from the theoretical optimum, then we're done. If the max iteration count has been reached, then we're also done. Otherwise, go to 7.

We break out of the loop once an error bound has been reached.

IV. Column generation

IV./1. Column generation algorithm (L. V. Kantorovich, 1939)

1. Start with only the simple patterns and solve the problem.
2. Minimize the number of sheets needed using the current patterns.
3. Set \(x\) to be the dual variables of the patterns.
4. Write up the dual of the sheet minimization problem.
5. (Column generation) Maximize the dual problem to obtain the best possible pattern (column) to use.
6. If the Dual Objective in Step 5 was 0 (*), then this is the optimal solution, STOP. Otherwise, go to 7.
7. Add the new pattern to the problem. Go to 2.

(*) If the dual objective is 0, then the new best pattern (column) we've generated isn't used. If not even the best new pattern is needed, then we must already have the optimal set of patterns.

Download the Lesson7_ColumnGeneration.mos Mosel model from here

IV./2. Code explanation

• forward procedure: Procedure to be defined later.
• forward function: Function to be defined later.
• Creating decision variables over unknown ranges:
  declarations
   RP: range
   use: dynamic array(RP) of mpvar
  end-declarations
  ...
  create(use(i))
  
• setparam("zerotol", 1e-6): Any value below \(10^{-6}\) will be considered to be 0. (This is useful for Step 6 of the Column Generation algorithm.)
• setparam("XPRS_CUTSTRATEGY", 0): XPress normally uses a mixture of Branch and Bound, and other IP solving techniques like Active Set, Dual Cutting Plane, Logarithmic Barrier, etc. methods. With this parameter, we're disabling its Branch and Bound solving methods, because we need the exact Dual problem of the original Primal.
• setparam("XPRS_PRESOLVE", 0): XPress normally attempts to presolve, a.k.a. simplify the problem by detecting and removing redundant constraints, tightening variable bounds. Again, we don't want this, because we need the exact Dual problem of the original Primal.
• loadprob(MinRolls): Reload the problem with objective function MinRolls (after adding/changing constraints or the objective).
• sethidden(Dem(j), true): Hide (remove) the Dem(j) demand constraints from the problem for now.
• sethidden(Dem(j), false): Unhide (readd) the Dem(j) demand constraints to the problem again.

IV./3. Exercise 2

a) Run the model! Go through it and try to understand the code.
b) Why is Pattern 8 the one we're using the most of? Why can't we use even more?
c) How about Pattern 6 and 10?
d) Was Pattern 9 ever the best (optimal) pattern to generate? If so, why are we using 0 of it?
e) Using pen and paper, write down the Primal problem!
f) Using pen and paper, write down the Dual problem!
g) Why can the Dual problem be thought of as a Knapsack problem? What's the knapsack? What are the items?
h) Print out how much total paper waste we have made!
i) Add the following constraint to the model: We can only cut each sheet into at most 3 parts. (Hints: The simple patterns have to change too. You can use the minlist function to get the minimum of two values. In the Knapsack subroutine, you have to set an additional constraint. You have to declare this constraint, and then later reset it to 0.)
j) What happens when you set this 3 to a 4 instead?

V. Bonus

An IPython Notebook file to calculate the possible patterns (and how many there are):

Download the cutting_stock_pattern_count.ipynb IPython Notebook file from here