---

Lesson 9
Constraint Programming

---

I. Mosel model: Sudoku

Download the Lesson9_Sudoku.mos Mosel model from here

Download the sudoku.dat Data file from here

We are solving a Sudoku with given numbers in the givenNumbers array. This is a sparse (dynamic) array, so its values are stored as an index + value pair, where each index is a (row, column) pair.

I/1. How to run the program

We are using a different solver now (XPress Kalis), which only allows for 50 decision variables with the free license. But our sudoku model has 9x9=81 cells, and 9 possibilities (binary variables) for each, which is 9x9x9=729 binary decision variables.

1. Connect to the university server with WinSCP: leibniz.math.bme.hu, use your university account name and password.
2. Copy the Lesson9_Sudoku.mos and sudoku.dat files to your university account file system. (Don't go into any subfolder, it makes the code execution a bit harder.)
3. Connect to leibniz.math.bme.hu again with PuTTY. Again you'll need your university account name and password.
4. Use the following commands to run your mosel file:
   

       source /usr/local/bin/xpvars.sh
       mosel Lesson9_Sudoku.mos

(You can right click to paste these commands.)

II. Constraint programming capabilities

On the surface this is similar to an IP model:

• Each decision variable is an integer (by default).
• You can use \(\le\), \(\ge\), \(=\) constraints.
• You can minimize or maximize an objective function with cp_minimise or cp_maximise.

But there are other capabilities:

• cpvar: Constraint programming variable, allows for the capabilities below.
• cplinctr: Linear constraint (like the objective function) in CP.
• cpctr: Any constraint in CP.
• setdomain: Sets the domain of a cpvar to a given range, set or array.
• setparam("kalis_default_lb", 3): Sets the default lower bound for all cpvar variables to 3.
• setparam("kalis_default_ub", 17): Sets the default upper bound for all cpvar variables to 17.
• <>: "Not equals." This can be used between cpvar variables. (Would give an error in LP or IP.)
• all_different: Creates constraints such that a set of cpvar variables have to all take on different values.
• occurrence(value,vars): Counts the number of occurrences of a value in vars. This can be set to \(\le\), \(\ge\), \(=\) to some other value.
• abs: The absolute value of a cpvar.
• distance: The (1D) distance between 2 cpvar variables.
• implies: If A cpctr should imply B cpctr. Returns a new cpctr.
• equiv: If A cpctr should be equivalent to B cpctr. Returns a new cpctr.
• cp_propagate: In CP, constraints are used actively to deduce infeasible values and delete them from the domains of variables. This mechanism is called constraint propagation. Each constraint computes impossible values for its variables and informs other constraints. This process continues as long as new deductions are made. This function gives true if the propagation was succesful, false if it wasn't (infeasible problem).
• cp_find_next_sol: Finds the next feasible solution. Returns false if there are none. (Note that both cp_propagate and this function need to return true in order to be a feasible solution.)
• getlb: Gets the lower bound of a cpvar after a solution was found.
• getub: Gets the upper bound of a cpvar after a solution was found.
• getsize: Gets the size of the range of possible values a cpvar can take on after a solution was found.
• is_fixed: True if a cpvar can only take on 1 possible value after a solution was found.
• cp_show_var: Returns the current domain of the cpvar passed in.

And so on. You can read about further capabilities in

<install location>/xpressmp/docs/solver/kalis/kalis_ug/kalisug.pdf
<install location>/xpressmp/docs/solver/kalis/kalis_ref/kalisref.pdf

II/1. Exercise 1

a) Find all the Constraint Programming capabilities in Lesson9_Sudoku.mos!
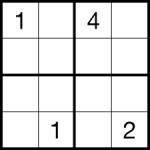
b) Start a new Mosel model! Set up the following 4 by 4 Sudoku pattern and solve it with kalis:

III. Scheduling Problems

This type of problem is a large topic in Combinatorial Optimization. The question is the following:

• Given \(J\) jobs and \(M\) machines, we would like to complete all jobs as fast as possible.
• Each job has some known length. Any machine can work on any job. Each machine can only work on 1 job at a time.
• What order should the jobs be completed in, and on which machines?
• Choice of objective function: sum of end times, minimax end time, ...
• Precedence: A DAG (Directed Acyclic Graph) that shows what jobs require what other jobs to finish. (Isn't necessarily part of every Scheduling Problem.)

Without precedence, and with the minimax objective function, this is very closely related to the multi-knapsack problem:


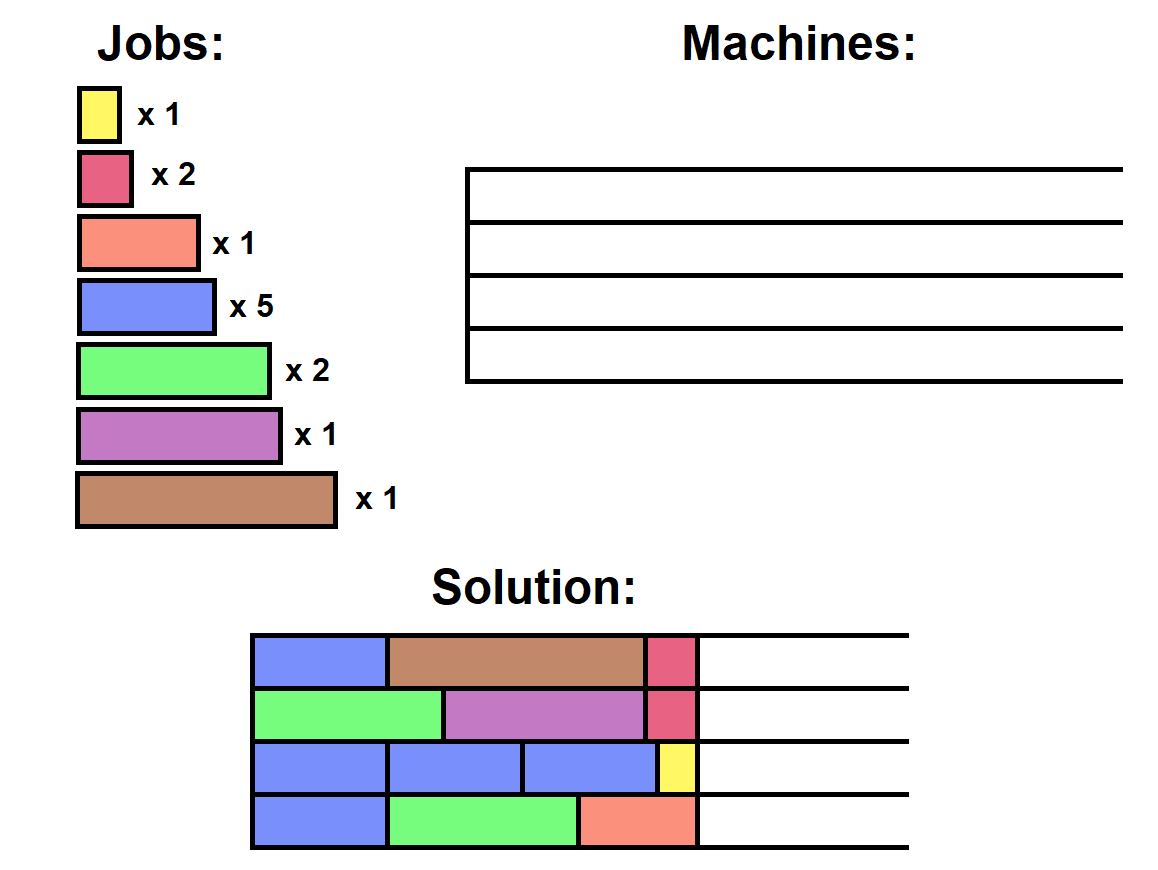
However in reality, a precedence graph is almost always required.

III./1. Simple Scheduling Problem in Mosel

Download the Lesson9_Scheduling.mos Mosel model from here

There are special scheduling parameters defined in XPress Kalis to make modelling easier:

• cpresource: Decision variable for machines/resources.
• cptask: Decision variable for jobs/tasks.
• set_resource_attributes: Defines what kind of resource we have. (Unary 0-1 or discrete with many threads.)
• getstart: Gets the starting time of a job. Can be used to set constraints.
• getend: Gets the ending time of a job. Can be used to set constraints.
• setduration: Sets the duration of a job.
• requires: Sets which job can use which machine(s).
• set_task_attributes: Sets the duration and the machine requirement in 1 command.
• setsuccessors, addsuccessors: Sets or adds the successors of a job defined by the precedence graph.
• setpredecessors, addpredecessors: Sets or adds the predecessors of a job defined by the precedence graph.
• getmakespan: Gets the total makespan of the jobs. (Minimax objective function.)
• cp_schedule: Can be used in place of cp_minimise or cp_maximise to simply find a feasible solution, instead of an optimal one.

III./2. Exercise 2

a) Find all the scheduling parameters in Lesson9_Scheduling.mos!
b) What would happen if we were to use 4 unary machines instead of 1 with 4 threads? We can accomplish this by changing res to res: array(1..M) of cpresource in declarations, and using 4 unary resources instead:

forall(m in 1..M) set_resource_attributes(res(m), KALIS_UNARY_RESOURCE, 1)

Moreover, we would need to change res to res(m) in the following for-loop, and add m in 1..M to the loop as well! How would this affect the solution?
c) Change back to 1 machine with 4 threads. (You can press undo as many times as you need.) Solve the same problem without using the set_task_attributes function! You will need to replace it with some other functions!
d) Add the following constraint: There is a planned shutdown 20 units of time after we're starting, lasting 3 units of time, affecting 2 of our machines. These machines won't be functioning. Any task started on these machines before the shutdown has to be finished before the shutdown. (Hint: Use 2 dummy jobs with set starting times and ending times!)
e) Add the following constraint: We cannot work on tasks that take at least 20 units of time between 24 and 26 units of time after starting, because of a high risk of an unexpected shutdown. (Hint: Set the domain of these tasks! The setdomain function also works with setdomain(x:cpvar, domain:set of integers).)

III./3. Multi-type machine Scheduling Problem in Mosel

Download the Lesson9_MultitypeScheduling.mos Mosel model from here

Download the multitype_scheduling.dat Data file from here

In this model, we've added the constraint that each job can only be done on a specific type of machine. For example, there are excavation jobs, piling vehicle driver jobs, carpentry jobs, concrete mixing jobs, etc.

• The finalize function finalizes the input (not yet defined) index sets with the length of the longest array that uses it.
• The requirement function can take 3 parameters as well: The task in question, how many machines it requires, what type of machine it requires.