ALKALMAZOTT MATEMATIKAI NAPOK

A BME MATEMATIKA INTÉZETBEN
 

Alkalmazott Matematika Határok Nélkül

Domokos Gábor 60 éves

Időpont: 2022. szeptember 5-6.
Helyszín: BME Díszterem

Meghívott előadók:

Mikaël Attal (University of Edinburgh)

Pebble size and shape as indicators of erosion and transport processes: breakthroughs from a mathematical perspective

Sediment grains (pebbles) are ubiquitous in our landscapes. We find them on the beach or along rivers. They can be used as construction materials, but can equally be tools of destruction when their transport is sudden and catastrophic (landslides, debris-flows). Each pebble, through its size and shape, records a history, from its birth as a fragment on a hillside to its resting place by a river, on a beach, or buried in a sedimentary basin. However, deciphering this history has been hindered by difficulties in collecting data and isolating the different processes that produce sediment grains and modify them during their transport downstream.
In this presentation, I will show how recent work, including the application of mathematical theories led by Gábor Domokos and colleagues, is bringing new insights into the processes that generate fragments and round them downstream, illustrated through specific examples, from the Himalaya to Mars.

Sir Michael Berry (University of Bristol)

The brilliant Raman stumbles

Raman argued that in a continuously varying layered medium, such as air above a hot road, a ray that bends so as to become horizontal must remain so, implying that the reflection familiar in the mirage cannot be explained by geometrical optics. This was a mistake (repeatedly made and corrected since 1799), as standard ray curvature arguments demonstrate. But a simple limiting process, in which the smoothly varying refractive index is approximated by a stack of thin discrete layers, is not quite straightforward because it involves a curious singularity. In contrast to individual rays, families of rays possess caustic (focal) singularities, which can sometimes be calculated explicitly. Mirage images involve families of families of rays.For important cases, waves decorating mirages are described by the universal Airy functions Ai and Bi, and can be calculated exactly

Snorre Christiansen (University of Oslo)

Finite element spaces of metrics with nice curvature

Given a triangulation of a 2D domain we construct a space of piecewise polynomial metrics, such that the linearized scalar curvature can be characterized as certain piecewise polynomial fields. The kernel of the linearized curvature operator can also be characterized as a space of deformations of given vectorfields. The three spaces have degrees of freedom that relate to rigid motion valued cochains.

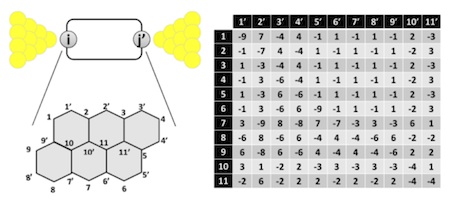
Silvio Decurtins (University of Bern)

Molecular materials at the interface between chemistry and physics

When researching at the interface between chemistry and physics, mathematical and geometrical methods are imperative, and thus many research topics demand the involvement of the mathematical art. Some examples will illustrate how the chemist can use applied mathematics to gain a deeper understanding of newly synthesized materials. Different dimensional structures and, among others, examples from the field of molecular magnetism and molecular electronics will be discussed. The figure illustrates how the directionality of charge transport through a single molecule can be represented by a matrix.

Kenneth Goldberg (University of California, Berkeley)

Adversarial Grasp Objects:  A new class of 3D solids

Learning-based approaches to robust robot grasp planning can grasp a wide variety of objects, but may be prone to failure on some objects. Inspired by recent results in computer vision, we define a class of “adversarial grasp objects" that are physically similar to a given object but significantly less ”graspable” in terms of a specified robot grasping policy.  We present three algorithms for synthesizing adversarial grasp objects under the grasp reliability measure of Dex-Net 1.0 for parallel-jaw grippers: 1) two analytic algorithms that perturb vertices on antipodal faces (one that uses random perturbations and one that uses systematic perturbations), and 2) a deep-learning-based approach using a variation of the Cross-Entropy Method (CEM) augmented with a generative adversarial network (GAN) to synthesize classes of adversarial grasp objects represented by discrete Signed Distance Functions. The random perturbation algorithm reduces graspability by 32%, 12%, and 32% for intersected cylinders, intersected prisms, and ShapeNet bottles, respectively, while maintaining shape similarity using geometric constraints. The systematic perturbation algorithm reduces graspability by 32%, 11%, and 21%; and the GAN reduces graspability by 22%, 36%, and 17%, on the same objects. We use the algorithms to generate and 3D print adversarial grasp objects. Simulation and physical experiments confirm that all algorithms are effective at reducing graspability.

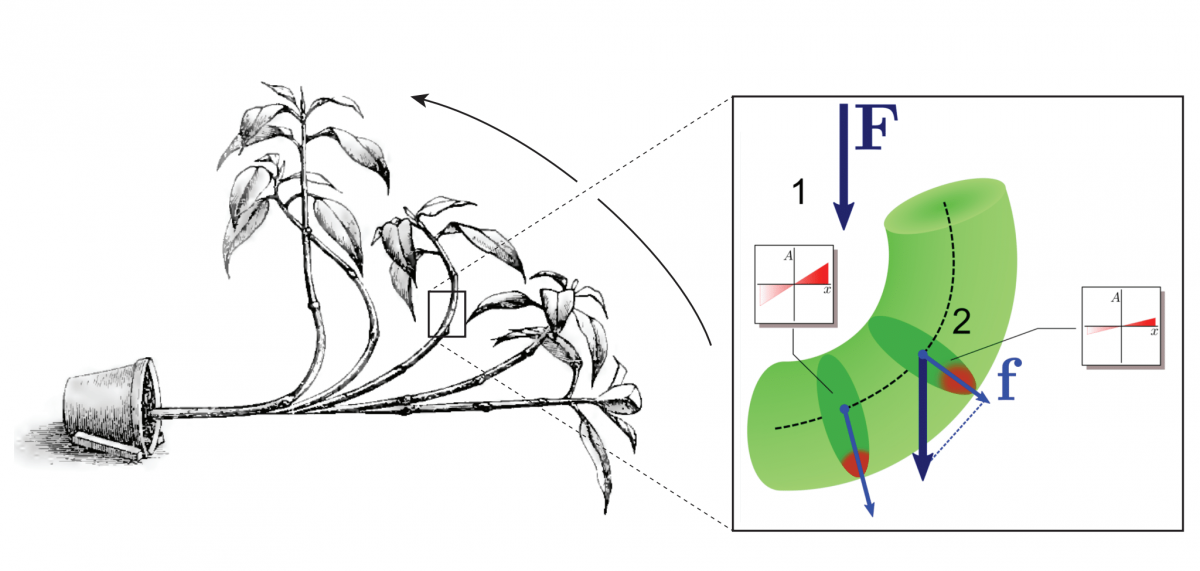
Alain Goriely (University of Oxford)

Modeling and understanding the motion of plants: An application of Gábor’s approach to natural phenomena

Many of Gábor Domokos’ works are inspired by simple observation of patterns appearing in nature and related to shape and motion. In this talk, I will apply Gábor’s approach to plants. The shape, motion, and behaviour of plants have been a central theme of research dating back to the first mechanistic explanations of plant tropism in the 18th Century. This early research continued in the 19th Century and culminated with the work of Darwin on the movement and habits of climbing plants. Functionally, it is clear that to survive and to thrive, plants rely on their ability to sense multiple environmental signals, such as gravity or light, and respond to them by growing in a particular direction and changing their shape. To do so, the signals must be transduced down to the cellular level to create the physical deformations leading to shape changes. In this talk, I will propose a general mathematical theory of tropism that takes multiple stimuli and show how they drive tissue-level growth and remodelling, thus modifying the plant shape and position with respect to the stimuli. This feedback loop is dynamically updated to understand the response to individual stimuli or the complex behaviours generated by multiple stimuli such as canopy escape or pole wrapping for climbing plants.

George Haller (ETH Zürich)

Equation- and data-driven nonlinear model reduction

Determining the forced response of very large, nonlinear mechanical systems remains a major challenge despite advances in computational power. Projection-based model reduction techniques have been in use for this purpose but they rely on ad hoc mode selection and produce a priori unknown errors. In this talk, I discuss a recent mathematical alternative to these approaches based on spectral submanifolds (SSMs), which are very low dimensional, attracting invariant surfaces in nonlinear systems. Reduction to SSMs turns out to yield previously unimaginable speed-ups in solving large finite-element models. Very recent results also show that SSMs and their reduced dynamics can be constructed directly from data. I will illustrate these results on high-dimensional mechanical systems and experimental data sets.

Timothy J Healey (Cornell University)

The inverse-deformation approach to fracture

We propose a one-dimensional, nonconvex elastic constitutive model with higher gradients that can predict spontaneous fracture at a critical load via a bifurcation analysis. It overcomes the problem of discontinuous deformations without additional field variables, such as damage or phasefield variables, and without a priori specified surface energy. Our main tool is the inverse deformation, which can be extended to be a piecewise smooth mapping even when the original deformation has discontinuities describing cracks opening. We exploit this via the inverse-deformation formulation of finite elasticity due to Shield and Carlson, including higher gradients in the energy. The problem is amenable to a rigorous global bifurcation analysis in the presence of a unilateral constraint. Fracture under hard loading occurs on a bifurcating solution branch at a critical applied stretch level, with a sudden drop to zero stress. Fractured solutions are found to have sharply defined cracks with surface energy arising from higher gradient effects.

János Kertész (Central European University)

Opinion dynamics and algorithmic bias

The evolution of opinions on virtual platforms, such as online social networks, is subject to radically different constraints than under traditional circumstances, like in face-to-face communication. By means of personalized, content filtering algorithms, online social platforms target and control the information individuals receive. This is usually done by collecting behavioral data on an individual's preferences, and then filtering incoming content from the rest of the social network, amounting to a so-called “algorithmic bias”. This new type of socio-technical bias can strongly impact the evolution of behavior, opinions, and norms in a population of individuals, who are often unaware of the role of algorithms in their interactions. Collective social phenomena like “echo chambers”, fragmentation and polarization of opinions, increasingly visible features of the global socio-political landscape, are likely promoted by algorithmic bias mechanisms. We explore the effect of online algorithmic bias on opinion dynamics by using simple models and characterize the bias intensity by the probability by which the platform chooses not to show content to an individual coming from users of the opposite state or opinion. We use theoretical tools of binary-state models, including the approximate master equation framework as well as numerical simulation for realistic networks including empirical social networks. We focus on the majority-vote and the noisy voter models as prototypical opinion-formation rules. The models show rich behavior with continuous and discontinuous transitions between coexistence-consensus-polarization states, depending on model types, bias intensity and network structure. Our results show that the link between online algorithmic bias and collective social behavior, although nuanced, can be modeled systematically, and highlights the complementary roles of filtering algorithms, rules of interaction, and network structure in the emergence of polarized information spreading.

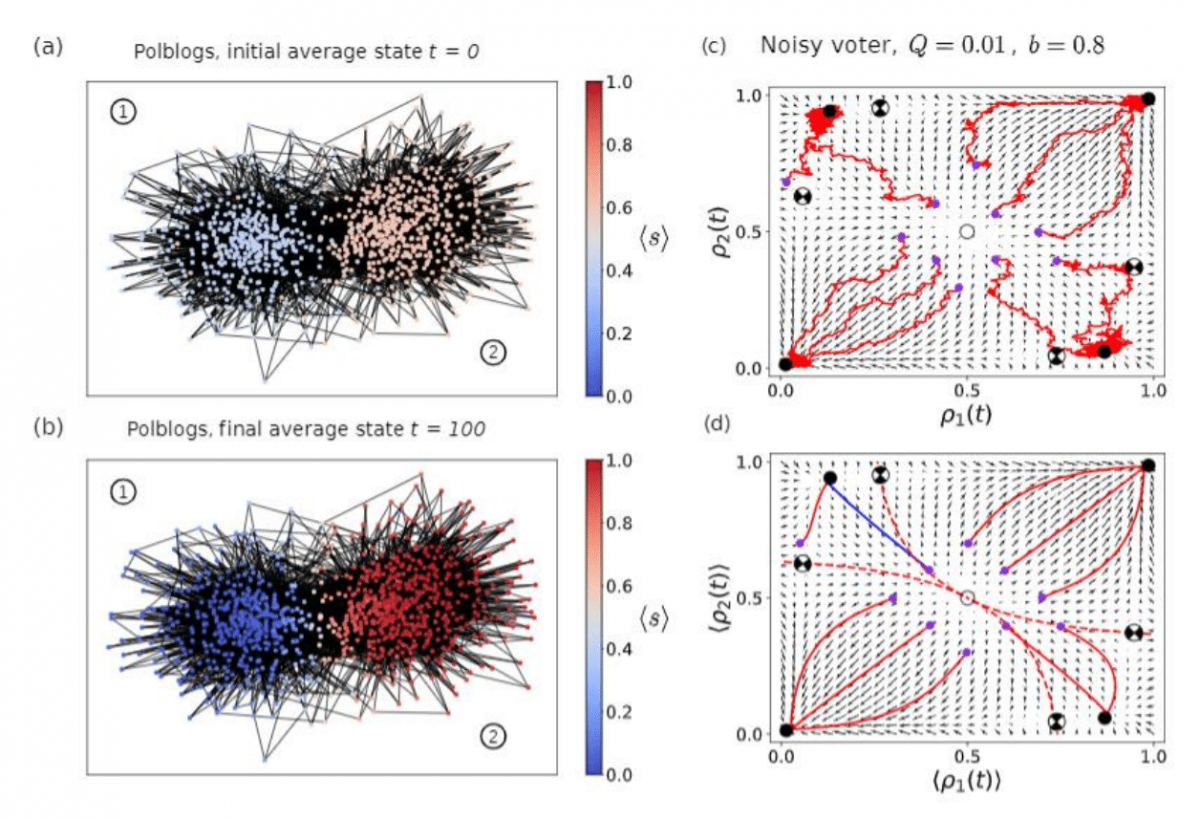
Binary opinion dynamics (majority vote model) on the real network of the American political blogosphere. (a) Average initial condition. (b) Average final state. The color code indicates the increase in polarization, the levels of noise (Q) and bias (b) are the same as on the panels on the right-hand side. (c) Map of the fixed point (fp) structure and the flows as a function of the initial conditions; ρ1 and ρ2 are the densities of opinion 1 in community 1 and 2, respectively. Empty circle: unstable fp, full circle: stable fp, circle with X: saddle point. Blue dots are initial conditions.Individual trajectories are shown. (d) The same as (c) with average trajectories.

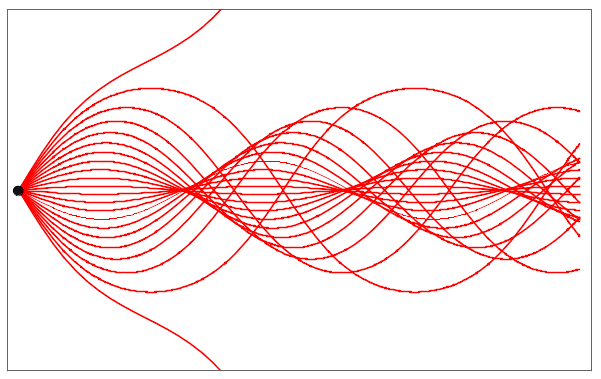
Boris Khesin (University of Toronto)

The golden ratio and hydrodynamics

There are useful and useless golden ratios. The useful one helps in traffic. The useless and rather mysterious one arises in hydrodynamics of point vortices, which we discuss in more detail. Furthermore, similar vortex structures arise in Charlie Chaplin's smoke ring challenge and in the singularity problem in higher-dimensional fluid dynamics.

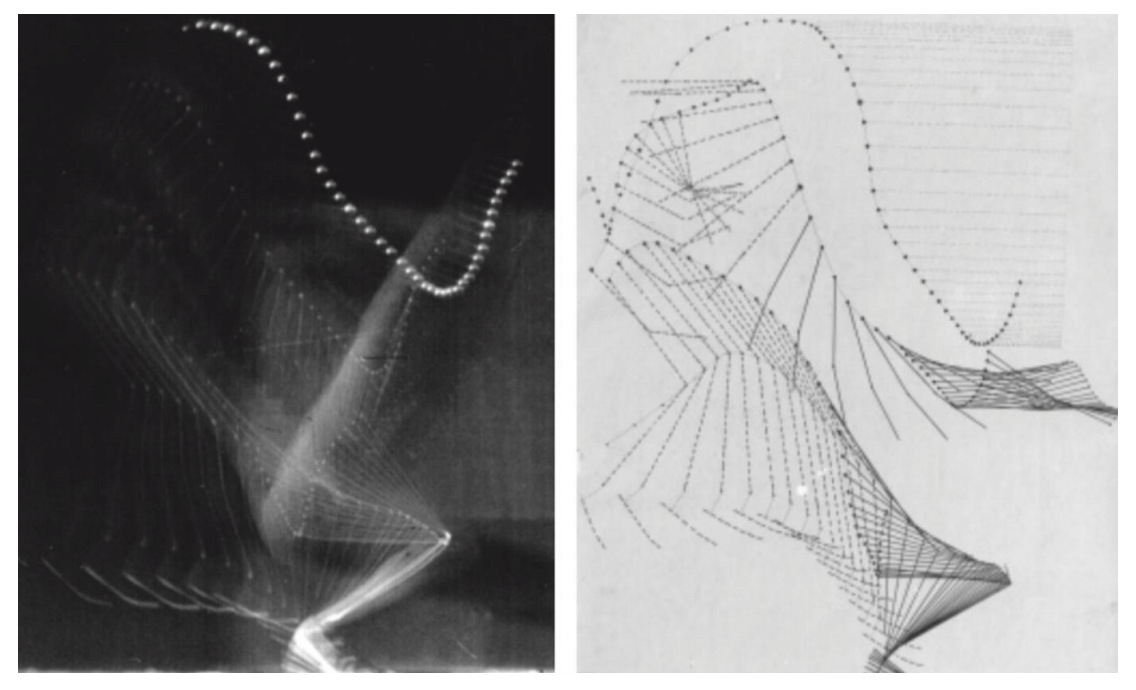
Ilona Kovács (Eötvös University)

From Muybridge to Marey: The evolution of skeletal shape representations in vision

Skeletal representations of shape, such as Voronoi diagrams or the medial axis transform are extremely useful tools in digital image processing today. It is less recognized, however, that these have been used in psychology as well, namely, in understanding how the brain processes information about shape, and in particular, biological shape. The growth and movement of living things is a complex process and it requires sparse representations that optimize space-time resolution. In this talk, I will bring examples from the history of photography to illustrate the beautiful evolution of the medial axis representation that psychology later applied to understand our capacity to process the movement of biological shapes. The photographic illustrations are from the collection of College de France, Paris, on Etienne Jules Marey’s medical images from the 19th century. I hope that these illustrations will inspire researchers of morhodynamics to investigate the usefulness of skeletal representations for the study of our non-living environment as well.

Hinke M Osinga and Bernd Krauskopf (University of Auckland)

The geometry of a blender: the case of spaghetti in a can

Blenders are a geometric tool to construct robust recurring dynamics in a theoretical setting; one also speaks of wild chaos. A blender in 3D space has the peculiar property that 1D curves associated with its so-called stable manifold weave such a complicated pattern in space that these curves form an impenetrable carpet. We consider an explicit family of 3D Hénon-like maps and show that it exhibits a blender for a specific parameter range where the underlying 2D Hénon map has a full horseshoe. This means that the stable manifold of the blender is given by the closure of the 1D stable manifolds of two saddle points. These two 1D stable manifolds form a smooth interwoven structure in space that fully covers (a finite part of) a plane when projected in certain directions. We determine and illustrate this surprising geometrical object by computing extremely long pieces of the two global invariant manifolds. To this end, we combine advanced numerical techniques with the compactification of phase space. In a nutshell, we study the blender and its 1D stable manifold in a bounded cylinder: infinitely long spaghetti in a can.

Ferenc Kun (University of Debrecen)

Controlling fracture patterns and fragment shapes in shrinkage induced cracking

Shrinkage induced cracking is abundant in nature giving rise to the formation of spectacular polygonal crack patterns for instance in dried lake beds, in permafrost regions on Earth and Mars, and in cooling volcanic lava. The simplest realization of such crack patterns can be achieved in the laboratory by desiccating thin layers of dense suspensions such as coffee, clay, or calcium carbonate on a rigid substrate where the gradual solidification leads to shrinkage stresses and cracking. Recently, a promising method of the generation of controlled crack patterns has been suggested by applying mechanical excitation to dense suspensions before desiccation sets in. Due to its high technological potential, we investigate such possibilities of crack patterning in the framework of a discrete element model focusing on the temporal and spatial evolution of anisotropic crack patterns as a thin material layer gradually shrinks. In the model a homogeneous material is considered with an inherent structural disorder where anisotropy is captured by the directional dependence of the local cohesive strength. We demonstrate that there exists a threshold anisotropy below which crack initiation and propagation is determined by the disordered micro-structure, giving rise to cellular crack patterns. When the strength of anisotropy is sufficiently high, cracking is found to evolve through three distinct phases of aligned cracking which slices the sample, secondary cracking in the perpendicular direction, and finally binary fragmentation following the formation of a connected crack network. The anisotropic crack pattern results in fragments with a shape anisotropy which gradually gets reduced as binary fragmentation proceeds. The statistics of fragment masses exhibits a high degree of robustness described by a log-normal functional form at all anisotropies.

Sir Konstantin S Novoselov (University of Manchester)

Materials for the future

This lecture is the 2022 Neumann lecture at the Budapest University of Technology and Economics.

Sidney Redner (Santa Fe Institute)

Birds on a wire

We investigate the occupancy statistics of birds on a wire and its natural higher-dimensional generalizations.  In one dimension, birds land one by one on a wire and rest where they land.  Whenever a newly arriving bird lands within a fixed distance of already resting birds, these resting birds immediately fly away.  We determine the steady-state occupancy of the wire, the distribution of gaps between neighboring birds, and other basic statistical features.  We provide numerical results and conjectures for corresponding observables for this same process in higher dimensions.

István Scheuring (Centre for Ecological Research)

A strategic model of a host-microbe-microbe system reveals the importance of a joint host-microbe immune response to combat stress induced gut dysbiosis

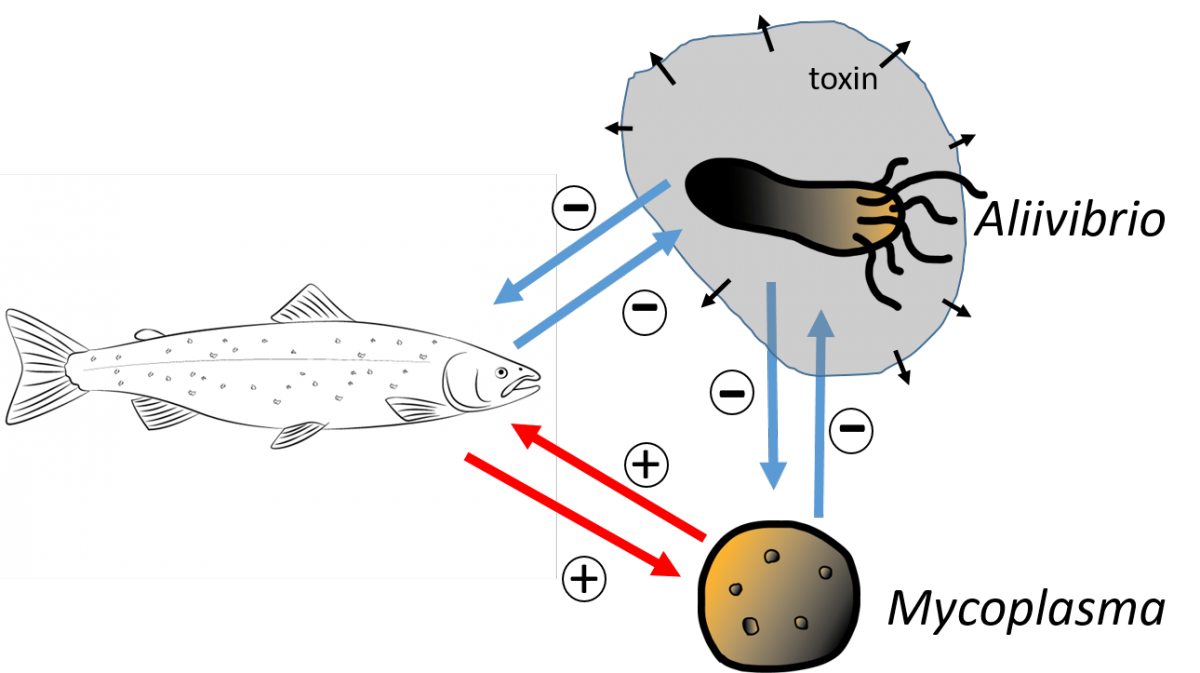
Microbiomes provide key ecological functions to their host; however, most host-associated microbiomes are too complicated to allow a model of essential host-microbe-microbe interactions. The intestinal microbiota of salmonids may offer a solution since few dominating species often characterize it. Healthy fish coexist with a mutualistic Mycoplasma sp. species, while stress allows the spread of pathogenic strains such as Aliivibrio sp. Even after a skin infection, the Mycoplasma does not recover; Aliivibrio sp. often remains the dominant species, or Mycoplasma-Aliivibrio coexistence was occasionally observed. We devised a model involving interactions among the host immune system, Mycoplasma sp. plus a toxin-producing pathogen. Our model embraces a complete microbiota community and is in harmony with experimental results that host-Mycoplasma mutualism prevents the spread of pathogens. Contrary, stress suppresses the host immune system allowing dominance of pathogens, and Mycoplasma does not recover after stress disappears.

Stanislav Smirnov (University of Geneva)

How the lizard got its colors

We will discuss how a Turing's reaction-diffusion process in a biological context leads to a rather surprising appearance of Ising-like colorings of the skin of Mediterranean lizards.

Gábor Stépán (Budapest University of Technology and Economics)

Delay sensitivity

The lecture will discuss cases when the stability properties of time delayed oscillators show extreme sensitivity to system parameters, especially to the time delays. These cases may seem to be mathematical curiosities, but they originate in relevant physical examples like the acceleration feedback in the wheeled inverted pendulum, the squealing sound in public address systems, or the hardware-in-the-loop tests of high-speed cutting.

Domokos Szász (Budapest University of Technology and Economics)

Sinai type billiards and statistical physics

The foundations of classical non-equilibrium statistical physics rely on Newtonian physics. (Analogy: in number theory one has to work in the realm of prime numbers.) History shows that the theory of Sinai-type billiards has been highly successful here despite of the apparent technical difficulties of the field. It is sufficient to mention achievements around (1) the Boltzmann-Sinai ergodic hypothesis, (2) Einstein’s theory of Brownian motion and (3) understanding energy transfer with the aim to create a rigorous bedrock for Fourier’s 1822 law of heat conduction. In the talk I will focus on item (2) (cf. [1,2]).

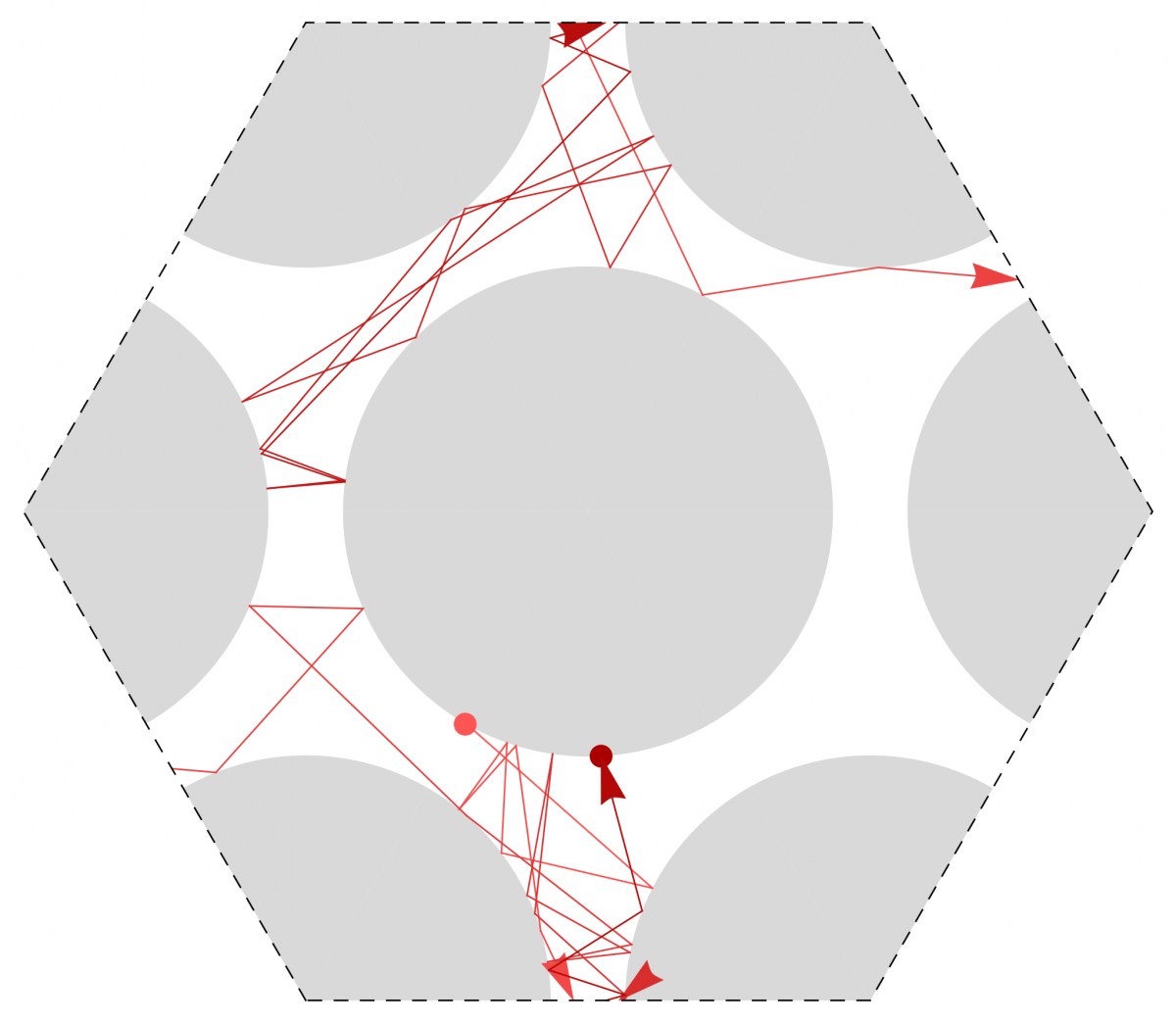
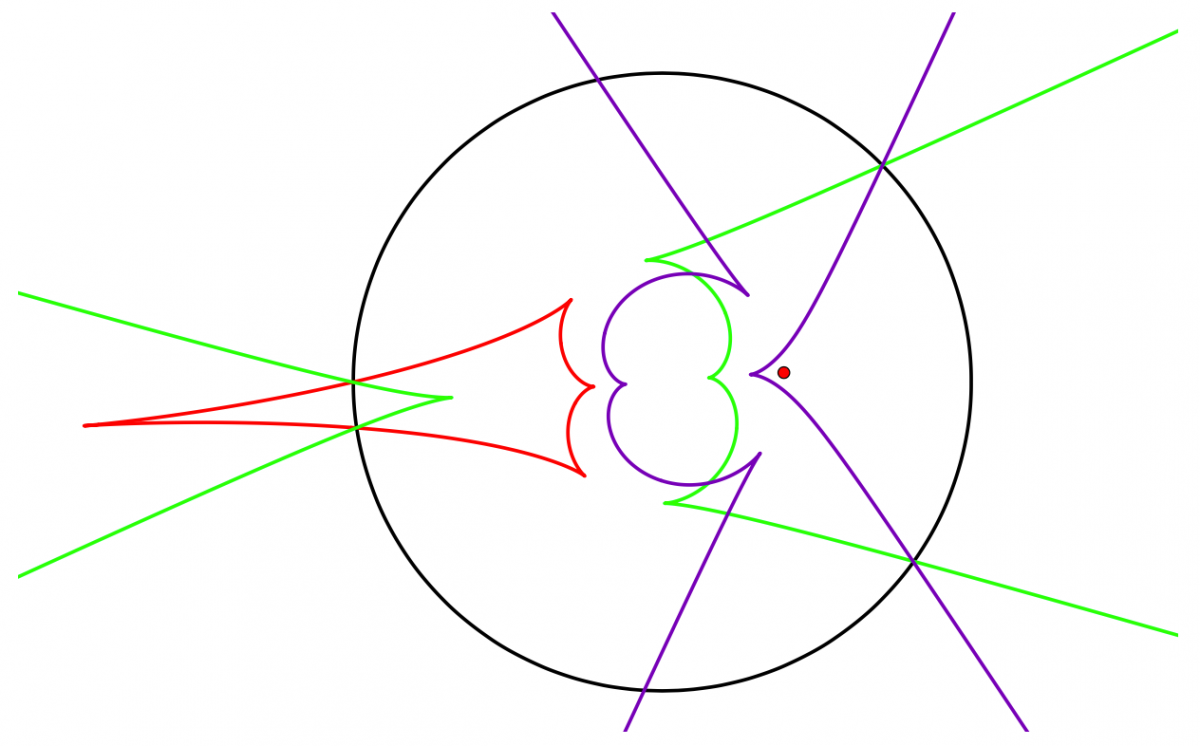
Sergei Tabachnikov (Pennsylvania State University)

Cusps of caustics by reflection

The boundary of a planar oval is an ideal mirror, and there is a point source of light inside the oval. Consider the rays of light that have undergone N reflections in the mirror, where N=1,2,... The envelope of this system of rays is the Nth caustic by reflection. I shall explain that, for every N, this caustic has at least four cusps. Similar problems for smooth convex surfaces were considered before: Caratheodory proved that the locus of points conjugated to a given point has at least four cusps, and Jacobi stated, in his "Lectures on dynamics", that this number is exactly four in the case of the ellipsoid (this is known as the "Last Geometric Statement of Jacobi"). Our problem is a billiard version of these differential geometric problems, and it belongs to an endless collections of results stemmed from and motivated by the classical 4-vertex theorem of Mukhopadhyaya.